python之CSF算法的示例分析

这篇文章给大家分享的是有关python之CSF算法的示例分析的内容。小编觉得挺实用的，因此分享给大家做个参考，一起跟随小编过来看看吧。

1. 引言

机载LiDAR可以获取快速、低成本地获取大区域的高精度地形测量值。为了获取高精度的地形数据（厘米级），对机载LiDAR点云数据进行“滤波”是一个非常重要的步骤。因此近二十年来，国内外学者提出了众多有效的自动滤波算法，大大降低了人力成本，提高了点云数据的应用效率。在博客：“点云地面点滤波(Progressive Morphological Filter)算法介绍（PCL库）”与“点云地面点滤波-progressive TIN densification(PTD)算法介绍”中分别对两种常用滤波器进行了介绍。
以往的众多算法滤波效果容易受到地形特征的影响（通常在复杂场景及陡峭地形区域滤波效果较差）且常常需要用户对数据有较为丰富的先验知识来进行设置滤波器中的各种参数。
为了解决这些问题，张吴明教授等人在2015年第三届全国激光雷达大会提出的“布料”滤波算法，本篇博客对其进行了简要介绍。

2. 基本思想

传统的滤波算法大多是考虑在坡度、高程变化之间的不同来进行区分地物点与地面点，而布料”滤波算法从一个完全新的思路来进行滤波，首先把点云进行翻转，然后假设有一块布料受到重力从上方落下，则最终落下的布料就可以代表当前地形。如下图所示，可以帮助我们进行理解。

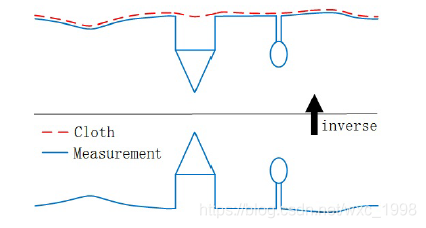
下方的蓝色图形代表原始测量值，对其进行翻转，红色虚线代表布料，可以反映地形的起伏。

3. CSF算法实现步骤

3.1 “布料”模拟

首先，定义了一个基本公式：

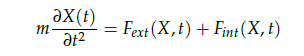
式中，X代表“布料”中的粒子在 t 时刻的位置，Fext(X,t)代表外部驱动因素（重力，碰撞等），Fint(X,t)代表内部驱动因素（粒子间的内部联系）。

即可以总结为“布料”粒子的位置受到Fext(X,t)与Fint(X,t)两方面因素的影响。

随后如下图所示，通过四个状态对“布料”粒子的移动过程进行说明。

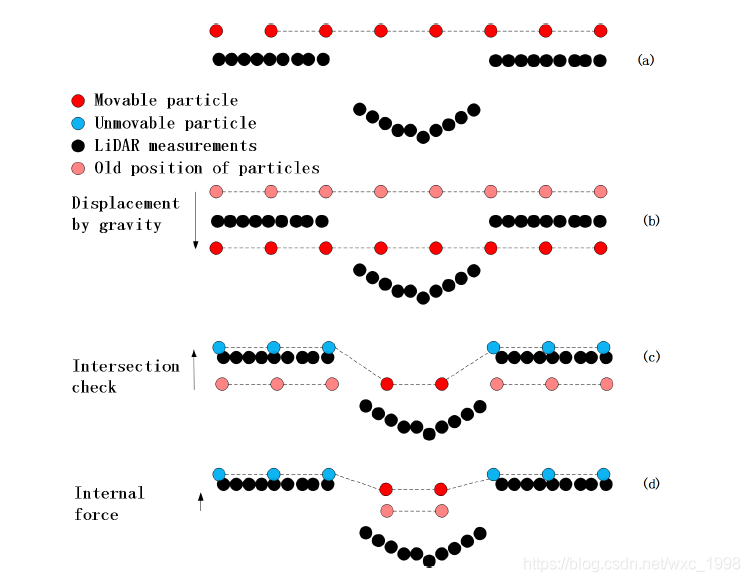
（a）为初始状态，假设一个虚拟的布放在翻转的LiDAR测量值上方。黑色点为LiDAR测量值，深红色点为可移动粒子。
（b）计算重力影响下对粒子产生的位移，由此一些粒子可能会出现在地面的下方。浅红色点为粒子的旧位置。
（c）相交检查，检查粒子新位置是否到达地面，如果已经到达地面则设置为不可移动。蓝色点代表粒子不可移动
（d）考虑“布料”的内部驱动，对现有的“可移动”粒子，根据邻近粒子所产生的“力”来进行移动新的位置。（如上图小房子处的可移动粒子）

2 外部/内部因素驱动

如3.1节中所述，粒子的位置移动包括外部/内部两方面的驱动因素，首先假设只有外部因素Fext(X,t)，并设置内部因素Fint(X,t)为0，可以得到以下公式：

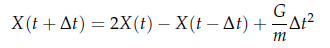
式中，m为粒子的重量，通常设置为1，△t 为时间步长。且由于G是一个常数，所以上式非常容易计算，只要给定一个△t 就可以计算出下一次迭代粒子所在的新位置。

为了约束粒子在反转表面空白区域的反转问题，作者又考虑了使用内部因素Fint(X,t) 。任意选取两个相邻的粒子，如果两个粒子都是 可移动 的，则令二者往相反的方向移动同样的距离；如果一个是不可移动的，则移动另一个；如果两者具有相同的高度，则不进行移动。
位移量可以通过下式进行计算：

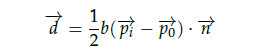
式中，d为粒子的位移量；当粒子可移动时，b等于1，不可移动时b等于0；pi为p0的相邻粒子，n是把点进行标准化到垂直方向上的单位向量（0，0，1）T。

移动过程如下图所示：

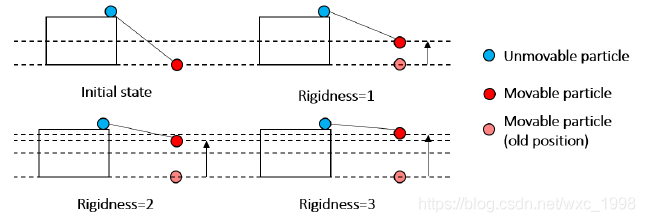
同时还引入了一个新的参数rigidness, RI，用来描述粒子的移动次数，RI为1时，则移动一次，且移动的距离是两个粒子之间高差的1/2；RI为2时，则移动两次，且移动3/4。类似的，RI为3时，移动三次，移动距离为两个粒子高差的7/8。RI的值越大，则“布料”就越硬，一般来说，平地需要设置RI的值较大，陡坡、山区需要设置的RI值较小。

3.3 具体实现

综上所述，布料模拟的简要步骤可以总结如下：
1）通过第三方软件去除原始LiDAR点云数据中的“孤立点”。
2）反转LiDAR点云。
3）初始布料格网，这时用户需要设置格网的大小（grid resolution, GR）。初始“布料”的位置通常在最高点的上方。
4）把所有LiDAR点与格网粒子投影到同一个水平面，并找到每一个粒子的最近邻点（corresponding point, cp），记录其投影前的高程（intersection height value, IHV）
5）对于每一个可移动的格网“粒子”，计算其受到重力影响产生的位移，并与当前粒子对应cp点的IHV进行比较，如果粒子的高度低于或者等于IHV，则把粒子的高度设置为IHV并设置为不可移动点。
6）对于每个格网“粒子”，计算其受到内部驱动因素影响所产生的的位移。
7）重复上述5）、6）步骤，直到所有粒子的最大高承诺变化足够小或者迭代次数到达用户的预先设置值，则停止模拟过程。
8）计算LiDAR点云与格网粒子之间的高度差异。
9）区分地面点与非地面点，如果LiDAR点与模拟粒子之间的距离小于预先设置的阈值hcc，则认为其是地面点，反之则认为其为非地面点。

3.4 后处理

上述方法处理过后对于平坦区域可以取得较好的效果，但是对于“陡坡”区域仍然会产生较大的误差，因为“布料”会由于其粒子间的内部约束而落在地面测量值的上方。如下图所示：

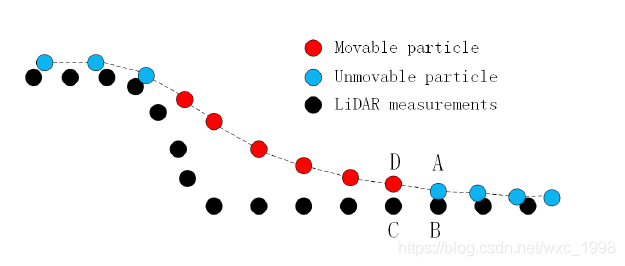
为了消除这些误差，可以通过一个后处理方法来解决。在每一个“可移动”粒子的四个邻接点中找到“不可移动”粒子，然后比较“最近邻点”之间的高程差，如果高程差值小于阈值hcp，则把“可移动”粒子移动到地面，并设置为不可移动。
例如，上图中的D点，找到了一个不可移动的粒子A，然后比较C,B之间的高程差值（对于D点、A点之间的最近邻点CP）。如果高程差值小于阈值hcp则待判断点D就被移动到C点，且被设置为不可移动。重复上述操作，直到所有的“可移动”粒子被正确处理。
如果逐行扫描“粒子”来进行实现此后处理操作，结果可能会受到特定扫描方向的影响。因此，作者采用了先建立一个“强连接元素集”（strongly connected components, SCC）包含一个关联的可移动粒子集。

如上图所示，每个SCC中包括两种粒子，第一种是至少包含一个近邻“不可移动”粒子（上图中的黄色点M1），第二种是近邻点中不包含“不可移动”粒子（上图中的红色点M2）。执行过程中使用外部的黄色点为“初始种子点”，通过“广度优先”的方式逐步向内遍历SCC。如上图中的从1-18点，实现了从边缘逐步向内部靠近处理过程，而不受扫描方向的影响。

感谢各位的阅读！关于“Python之CSF算法的示例分析”这篇文章就分享到这里了，希望以上内容可以对大家有一定的帮助，让大家可以学到更多知识，如果觉得文章不错，可以把它分享出去让更多的人看到吧！