卷积神经网络如何实现提取特征

图像在计算机中的存储

图像其实就是一个像素值组成的矩阵。

1、黑白或灰度图像如何存储在计算机中

在这里，我们已经采取了黑白图像，也被称为一个灰度图像。

这是数字8的图像。现在，如果我们进一步放大并且仔细观察，你会发现图像变得失真，并且你会在该图像上看到一些小方框。

这些小方框叫做 Pixels。我们经常使用的图像维度是X x Y。这实际上是什么意思？

这意味着图像的尺寸就是图像的高度（x）和宽度（y）上的像素数。

在这种情况下，高度为24像素，宽度为16像素。因此，此图像的尺寸将为24 x 16。尽管我们看到的是这种格式的图像，但计算机以数字的形式存储图像。

这些像素中的每一个都表示为数值，而这些数字称为像素值，这些像素值表示像素的强度。

对于灰度或黑白图像，我们的像素值范围是 0 到 255 ：接近零的较小数字表示较深的阴影，而接近255的较大数字表示较浅或白色的阴影。

因此，计算机中的每个图像都以这种形式保存，其中你具有一个数字矩阵，该矩阵也称为Channel。

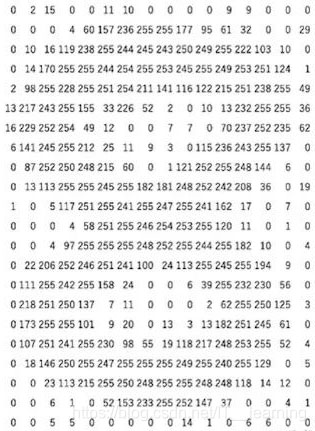
总结：

• 图像以数字矩阵的形式存储在计算机中，其中这些数字称为像素值。
• 这些像素值代表每个像素的强度：0代表黑色，255代表白色。
• 数字矩阵称为通道，对于灰度图像，我们只有一个通道。

2、彩色图像如何存储在计算机中

现在我们有了关于如何将灰度图像存储在计算机中的想法，让我们看一个彩色图像的示例。让我们以彩色图像为例，这是一条美女的图像：

该图像由许多颜色组成，几乎所有颜色都可以从三种原色（红色，绿色和蓝色）生成。

我们可以说每个彩色图像都是由这三种颜色或3个通道（红色，绿色和蓝色）生成。

这意味着在彩色图像中，矩阵的数量或通道的数量将会更多。

在此特定示例中，我们有3个矩阵：1个用于红色的矩阵，称为红色通道。

另一个绿色的称为绿色通道。

最后是蓝色的矩阵，也称为蓝色通道。

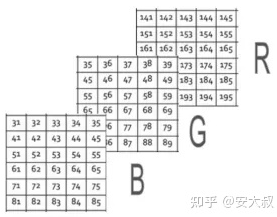
这些像素都具有从0到255的值，其中每个数字代表像素的强度，或者你可以说红色，绿色和蓝色的阴影。最后，所有这些通道或所有这些矩阵都将叠加在一起，这样，当图像的形状加载到计算机中时，它会是

N * H * W

其中 N 表示通道数（彩色图像 N 为 3），H 是整个高度上的像素数，W 是整个宽度上的像素数。在这种情况下，我们有3个通道R、G和B。在我们的示例中，彩色图像的形状将是 6 x 5 x 3，因为我们在高度上有6个像素，在宽度上有5个像素，并且存在3个通道。

矩阵的特征值与特征向量

这个式子要怎么理解呢？

首先得先弄清矩阵的概念：一个矩阵代表的是一个线性变换规则，而一个矩阵的乘法运行代表的是一个变换。

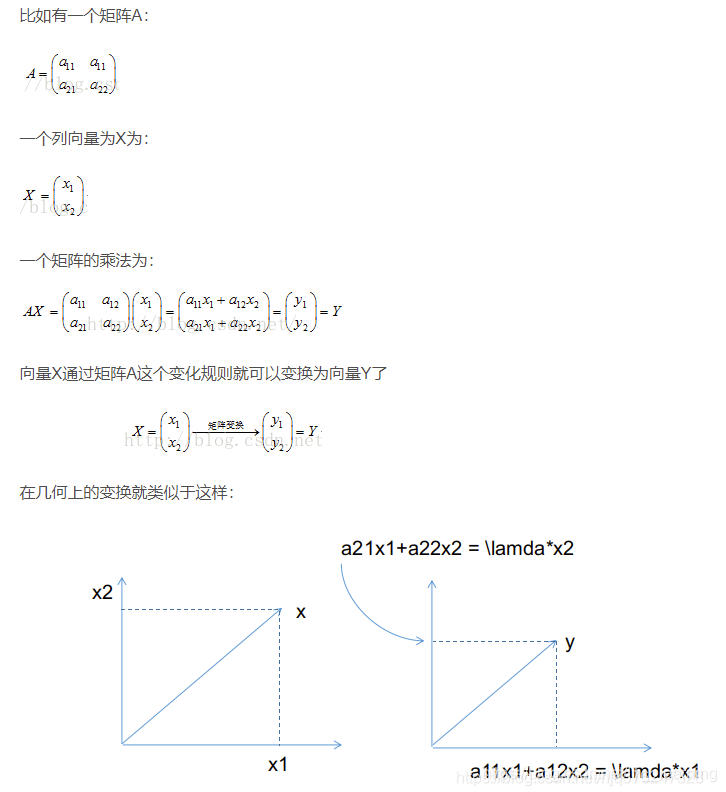
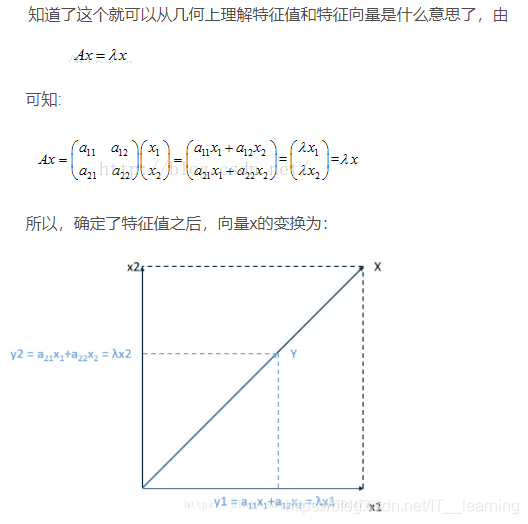
也就是说，我们有一个方阵（n x n），总能找到一些向量，这个矩阵跟这些向量的作用效果，只是对这个向量造成了拉伸的作用，换句话说，矩阵的作用跟一个系数的作用是等价的。

也就是如下这个式子：

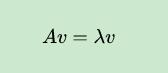
在图像处理中，有一种方法就是特征值分解。

我们都知道图像其实就是一个像素值组成的矩阵，假设有一个100x100的图像，对这个图像矩阵做特征值分解，其实是在提取这个图像中的特征，这些提取出来的特征是一个个的向量，即对应着特征向量。

而这些特征在图像中到底有多重要，这个重要性则通过特征值来表示。

比如 100x100 的图像矩阵A分解之后，会得到一个100x100的特征向量组成的矩阵Q，以及一个100x100的只有对角线上的元素不为0的矩阵E，这个矩阵E对角线上的元素就是特征值，而且还是按照从大到小排列的（取模，对于单个数来说，其实就是取绝对值），也就是说这个图像A提取出来了100个特征，这100个特征的重要性由100个数字来表示，这100个数字存放在对角矩阵E中。在实际中我们发现，提取出来的这100个特征从他们的特征值大小来看，大部分只有前20（这个20不一定，有的是10，有的是30或者更多）个特征对应的特征值很大，后面的就都是接近0了，也就是说后面的那些特征对图像的贡献几乎可以忽略不计。我们知道，图像矩阵A特征值分解后可以得到矩阵Q和矩阵E：

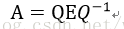
那么反推出去，把右边的三个矩阵相乘肯定也能得到矩阵A。既然已经知道了矩阵E中只有前20个特征值比较重要，那么我们不妨试试把E中除了前20个后面的都置为0，即只取图像的前20个主要特征来恢复图像，剩下的全部舍弃，看看此时会发生什么：

原图：【注意：特征值分解要求必须是nxn的方阵，如果不是行列相等的方阵，请使用奇异值分解】

只取前10个特征值：

只取前20个特征值：

只取前50个特征值：

只取前100个特征值：

我们可以看到，在只取前20个特征值和特征向量对图像进行恢复的时候，基本上已经可以看到图像的大体轮廓了，而取到前50的时候，几乎已经和原图像无异了。明白了吧，这就是所谓的矩阵的特征向量和特征值的作用。

所以归根结底，特征向量其实反应的是矩阵A本身固有的一些特征，本来一个矩阵就是一个线性变换，当把这个矩阵作用于一个向量的时候，通常情况绝大部分向量都会被这个矩阵A变换得“面目全非”，但是偏偏刚好存在这么一些向量，被矩阵A变换之后居然还能保持原来的样子，于是这些向量就可以作为矩阵的核心代表了。于是我们可以说：一个变换（即一个矩阵）可以由其特征值和特征向量完全表述，这是因为从数学上看，这个矩阵所有的特征向量组成了这个向量空间的一组基底。而矩阵作为变换的本质其实不就把一个基底下的东西变换到另一个基底表示的空间中么？

图像特征与特征向量

假设我们要判断一个人是男的还是女的，第一反应可能是“头发”，其次是“声音”，或者“衣着”之类的，一般通过以上3个特征就能非常直观地判断出来是男的还是女的。

但是呢，出题人A特别坏，出题人A说：这个人，他有一双明亮的大眼睛，有一头乌黑的头发，喜欢出入酒吧，一般十点钟上班，声音比较细腻，走路比较急，还有，喜欢吃零食，喜欢穿浅色衣服。

出题人B比较好，出题人B说：他头发比较长，说话比较温柔，穿的比较阳光，声线比较细。

我们一听B的说法，就很直观地觉得这个人八九不离十是位女生，而从A的判断中，我们还是模棱两个。这个就涉及到信息量的问题。A给的特征非常多，信息量很大，但是。。。似乎没什么用，而B给的特征少，但是基本足够了。就像图1，他的数据分布特别散漫，而图3的分布相对集中，是一个道理的。相对于信息量大的特征，我们去挑选特征、做出判断是非常困难的。

所以！！！我们就需要想办法对特征做特征提取。也就是说，提取主要的、关键的特征就够了！！！而这个提取的方法就是：特征向量！！！

以椭圆举例：

以上几个图，全都可以分类为椭圆，但是因为形状各异，导致数据也是不对称的，尤其体现在rgb值上（当然在对图像的数据处理，还有很多，比如subtraction，BN），其次体现在在各个轴的投影。但是，如果如果我们可以对它做旋转，缩放，平移等操作，变成如下的图：

那，是不是就非常好辨认了，而且数据也非常集中，至少在某一维度上。于是乎，我们就需要去找这么一个特征向量。卷积的过程，就是通过反向传播，无限去拟合这么一个非常非常非常逼近的特征向量集（这个特征向量集其实就是咱们的卷积核）！！！！为什么是特征向量集呢（其实单个特征向量（一个列向量或者行向量）也行）？因为一个列向量，我们只能在一种维度做变换，多个列向量，就意味着多个维度联合进行特征提取或者曰之为特征映射。

总结一下：卷积核 ≈ 特征向量集，反向传播 ≈ 求解特征向量集，我们的图片 ≈ 矩阵A，注意，这些概念不是等价的，只是用易懂的方式去解释这些原理。

卷积神经网络中，第一步一般用卷积核去提取特征，这些初始化的卷积核会在反向传播的过程中，在迭代中被一次又一次的更新，无限地逼近我们的真实解。其实本质没有对图像矩阵求解，而是初始化了一个符合某种分布的特征向量集，然后在反向传播中无限更新这个特征集，让它能无限逼近数学中的那个概念上的特征向量，以致于我们能用特征向量的数学方法对矩阵进行特征提取。

卷积提取特征

卷积核（滤波器，convolution kernel）是可以用来提取特征的。图像和卷积核卷积，就可以得到特征值，就是 destination value。

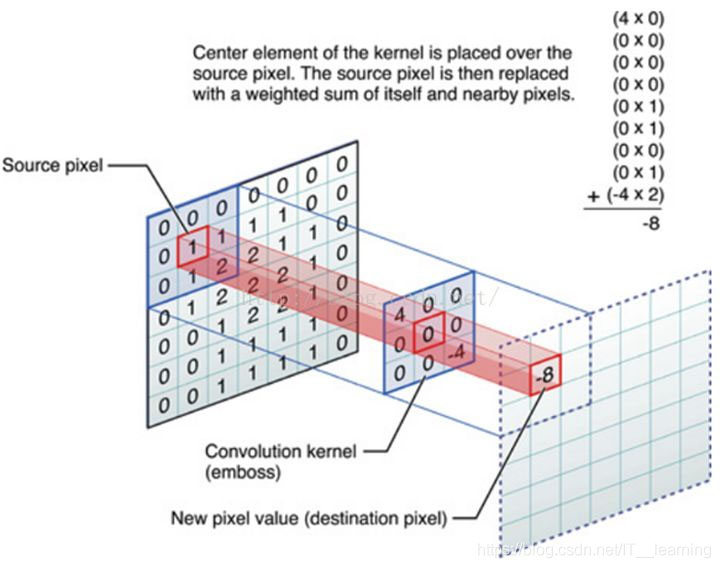
卷积核放在神经网络里，就代表对应的权重（weight)。

卷积核和图像进行点乘（dot product)，就代表卷积核里的权重单独对相应位置的Pixel进行作用。

至于为什么要把点乘完所有结果加起来，实际上就是把所有作用效果叠加起来。就好比前面提到的RGB图片，红绿蓝分量叠加起来产生了一张真正意义的美女图。

假设我们已经知道 RGB 的三个对应分量以及卷积核（里面的数字即相当于权重）：

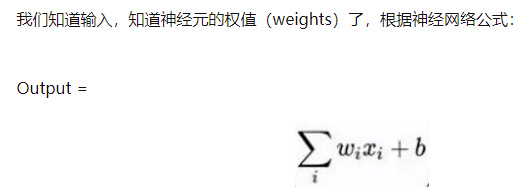
于是发生以下过程：

我们卷积输出的特征图（feature map）,除了特征值本身外，还包含相对位置信息，比如人脸检测，眼睛，鼻子，嘴巴都是从上到下排列的，那么提取出的相应的特征值也是按照这个顺序排列的。

因此我们实现卷积运算的方式就是：从左到右，每隔 stride（步幅）列 Pixel，向右移动一次卷积核进行卷积；从上到下，每隔 stride（步幅）行 pixel，向下移动一次卷积核，移动完成。

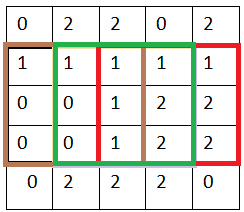
就这样，我们先从左到右，再从上到下，直到所有 pixels 都被卷积核过了一遍，完成输入图片的第一层卷积层的特征提取。

总结

以上为个人经验，希望能给大家一个参考，也希望大家多多支持编程网。