目录概述原理经典实现一个其他非典型实现示例波形调整概述 引述维基百科的介绍: Perlin噪声(Perlin noise,又称为柏林噪声)指由Ken Perlin发明的自然噪声生成算
引述维基百科的介绍:
Perlin噪声(Perlin noise,又称为柏林噪声)指由Ken Perlin发明的自然噪声生成算法,具有在函数上的连续性,并可在多次调用时给出一致的数值。 在电子游戏领域中可以透过使用Perlin噪声生成具连续性的地形;或是在艺术领域中使用Perlin噪声生成图样。
维基百科的介绍相当的官方,其实可以理解为一个随机函数,不过有以下两个特点:
它适用于希望给定连续的输入,能够给出相对连续的随机输出。(例如,模拟自然地形生成:想象地形不能前一步是高山,脚下是深谷,后一步又是高山这种连续剧烈的变化)
随机函数噪声:
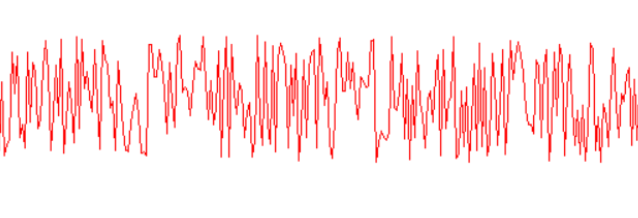
柏林噪声:

对于有经验的同学来说,一提到“平滑”,直觉上就会想到插值、平滑函数等。没错,柏林噪声其实就是使用插值、平滑函数,有时会在此基础上使用倍频,波形叠加(傅里叶变换)等方法对波形调整。
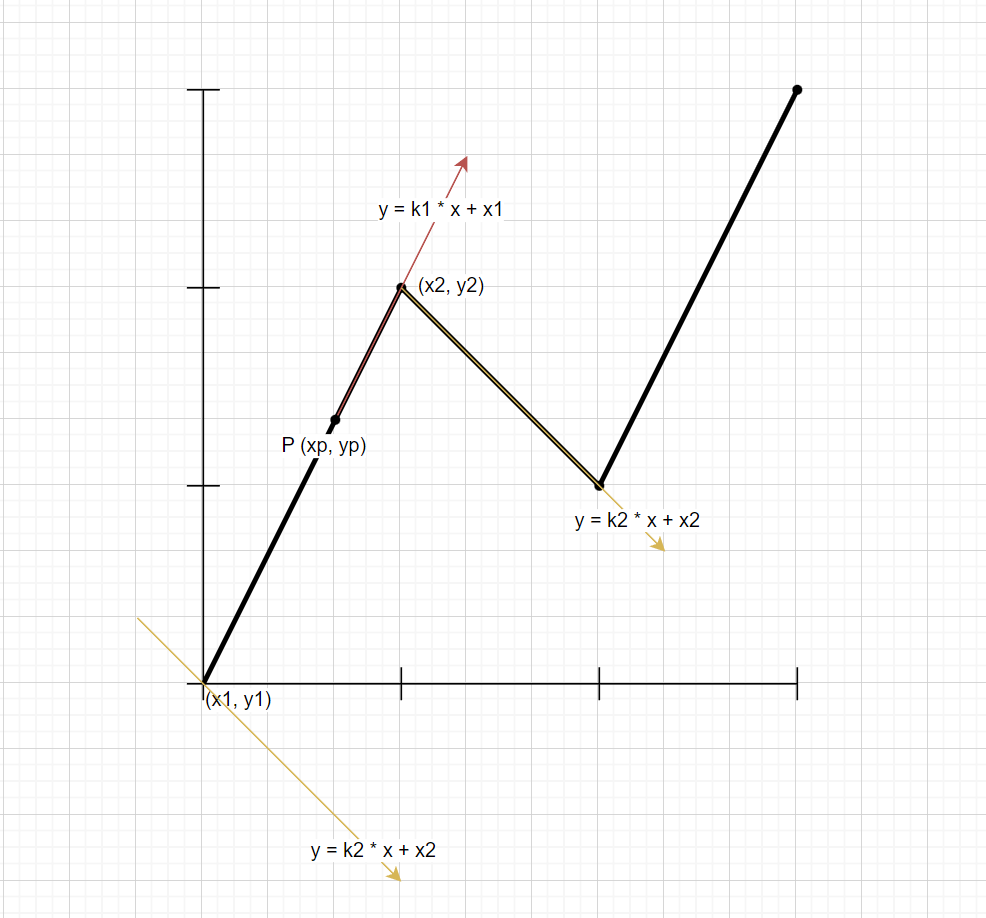
先把复杂问题简单化,考虑一个一维的柏林噪声生成:
上面提到了插值,插值首先要有值:静态生成一组随机数,在一个坐标系中每单位距离散落一个随机数。不妨令:rands是这个随机数数组,上图中y1 = rands[0], y2 = rands[1], ...,x2 - x1 = delta_x = 上述的单位距离,建立一个坐标系。
对于散落在[0, rands.Len - 1]区间的某个值n来说([rands.Len-1, rands.Len]区间对应的x的点规定不能取到,因为下面计算会推到rands[n + 1]),假设n对应上图P点则有:
Noise(P) = Y1 + (Y2 - Y1) * F((xp - x1)/(delta_x))
理解下这个公式:
Y1指红色的那个函数表达式(N),Y2指黄色的(N + 1)
Noise(P)类型插值函数: Lerp = yn + (yn+1 - yn) * t, t 取值 [0, 1],在这里:
这里的F是指平滑函数,上述(t)可知F在[0,1]的输出也必须在[0,1]区间内,通常F(x) = 6 * x^5 - 15 * x^4 - 10 * x^3,顾名思义就是对输入进行平滑,函数图像如下:
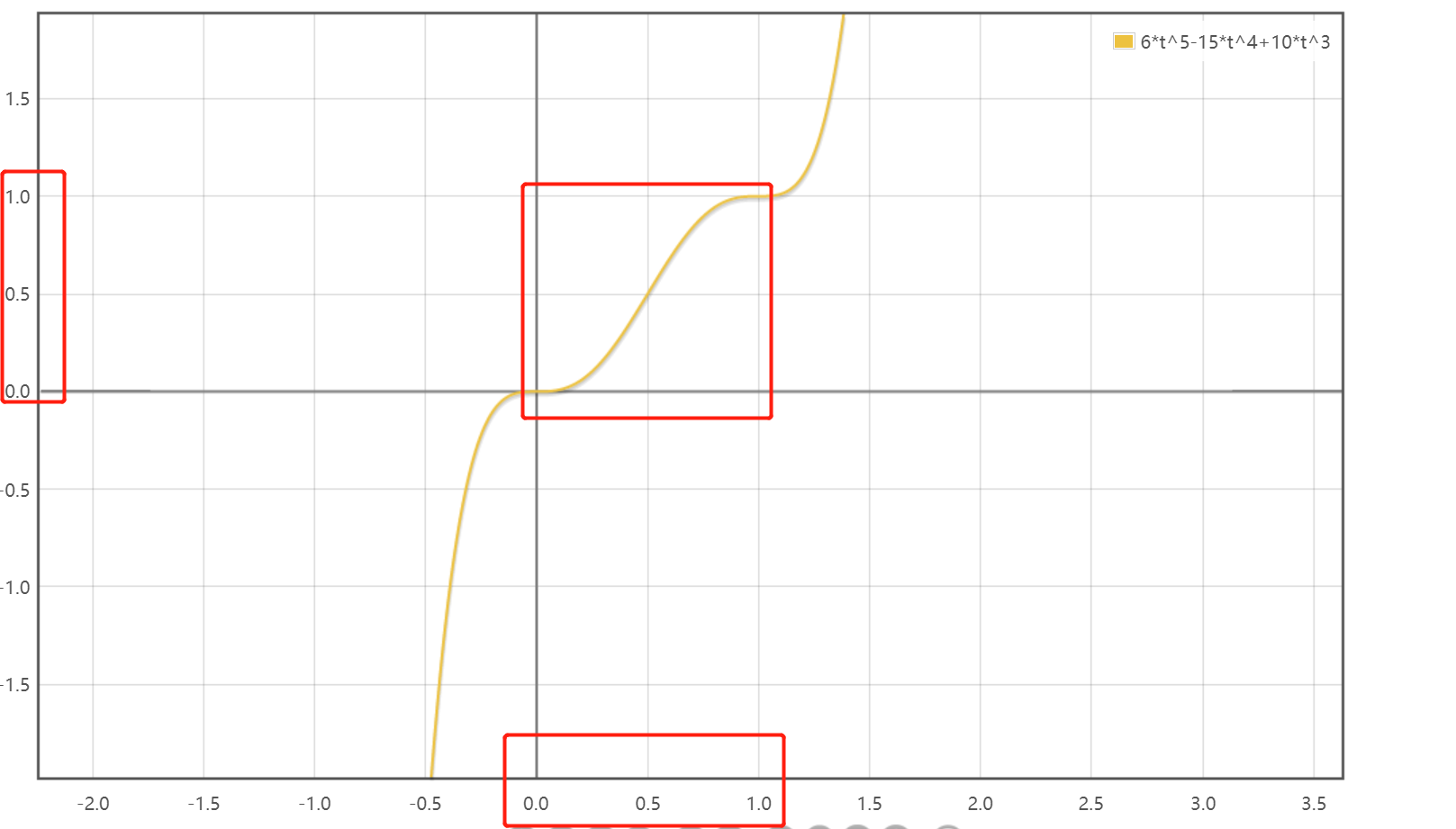
带入数据来算:
Noise(p) = Y1(xp) + (Y2(xp) - Y1(xp)) * F((xp - x1)/(delta_x))
就不展开了
再来思考下它的实现原理:
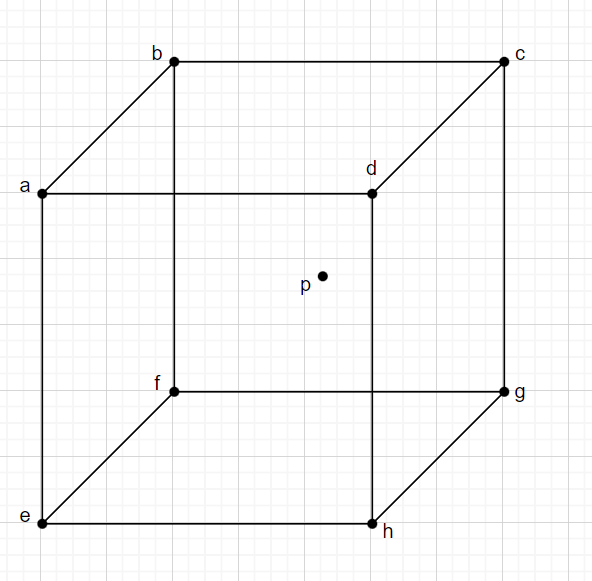
其思路可以拓展到2维、3维,以2维举例:
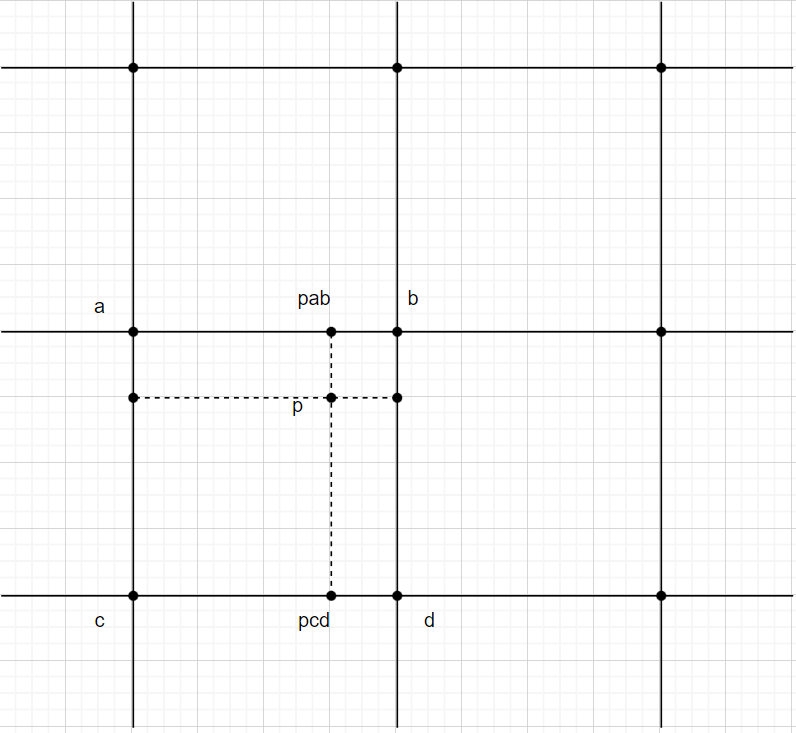
p落在abcd组成的2维网格中,其实可以视为3次1维的计算:分别计算pab、pcd所在1维直线(ab、cd)的结果,在此基础上计算pad、pcd所在的线上p点的结果。这个计算会在下面的代码实现中更加具象化体现出来。(注意有一点计算是不一样的,一维中y = kx + b计算两个点之间的影响在2维空间不适用,点会受到2个维度的影响,具体看下面实现中的示例)
static int p[512] = {
151,160,137,91,90,15,
131,13,201,95,96,53,194,233,7,225,140,36,103,30,69,142,8,99,37,240,21,10,23,
190, 6,148,247,120,234,75,0,26,197,62,94,252,219,203,117,35,11,32,57,177,33,
88,237,149,56,87,174,20,125,136,171,168, 68,175,74,165,71,134,139,48,27,166,
77,146,158,231,83,111,229,122,60,211,133,230,220,105,92,41,55,46,245,40,244,
102,143,54, 65,25,63,161, 1,216,80,73,209,76,132,187,208, 89,18,169,200,196,
135,130,116,188,159,86,164,100,109,198,173,186, 3,64,52,217,226,250,124,123,
5,202,38,147,118,126,255,82,85,212,207,206,59,227,47,16,58,17,182,189,28,42,
223,183,170,213,119,248,152, 2,44,154,163, 70,221,153,101,155,167, 43,172,9,
129,22,39,253, 19,98,108,110,79,113,224,232,178,185, 112,104,218,246,97,228,
251,34,242,193,238,210,144,12,191,179,162,241, 81,51,145,235,249,14,239,107,
49,192,214, 31,181,199,106,157,184, 84,204,176,115,121,50,45,127, 4,150,254,
138,236,205,93,222,114,67,29,24,72,243,141,128,195,78,66,215,61,156,180,
151,160,137,91,90,15,
131,13,201,95,96,53,194,233,7,225,140,36,103,30,69,142,8,99,37,240,21,10,23,
190, 6,148,247,120,234,75,0,26,197,62,94,252,219,203,117,35,11,32,57,177,33,
88,237,149,56,87,174,20,125,136,171,168, 68,175,74,165,71,134,139,48,27,166,
77,146,158,231,83,111,229,122,60,211,133,230,220,105,92,41,55,46,245,40,244,
102,143,54, 65,25,63,161, 1,216,80,73,209,76,132,187,208, 89,18,169,200,196,
135,130,116,188,159,86,164,100,109,198,173,186, 3,64,52,217,226,250,124,123,
5,202,38,147,118,126,255,82,85,212,207,206,59,227,47,16,58,17,182,189,28,42,
223,183,170,213,119,248,152, 2,44,154,163, 70,221,153,101,155,167, 43,172,9,
129,22,39,253, 19,98,108,110,79,113,224,232,178,185, 112,104,218,246,97,228,
251,34,242,193,238,210,144,12,191,179,162,241, 81,51,145,235,249,14,239,107,
49,192,214, 31,181,199,106,157,184, 84,204,176,115,121,50,45,127, 4,150,254,
138,236,205,93,222,114,67,29,24,72,243,141,128,195,78,66,215,61,156,180
};
static float3 grads[12] = {
{1,1,0},
{-1,1,0},
{1,-1,0},
{-1,-1,0},
{1,0,1},
{-1,0,1},
{1,0,-1},
{-1,0,-1},
{0,1,1},
{0,-1,1},
{0,1,-1},
{0,-1,-1}
};
float grad(int hash, float x, float y, float z)
{
float3 v3 = float3(x,y,z);
hash = hash & 0xb;
return dot(grads[hash],v3);
}
int inc(int num) {
num++;
return num;
}
float fade(float t) {
return t * t * t * (t * (t * 6 - 15) + 10);
}
float perlin(float x,float y,float z)
{
int xi = (int)x & 255;
int yi = (int)y & 255;
int zi = (int)z & 255;
float xf = x - xi;
float yf = y - yi;
float zf = z - zi;
float u = fade(xf);
float v = fade(yf);
float w = fade(zf);
int aaa, aba, aab, abb, baa, bba, bab, bbb;
aaa = p[p[p[ xi ]+ yi ]+ zi ];
aba = p[p[p[ xi ]+inc(yi)]+ zi ];
aab = p[p[p[ xi ]+ yi ]+inc(zi)];
abb = p[p[p[ xi ]+inc(yi)]+inc(zi)];
baa = p[p[p[inc(xi)]+ yi ]+ zi ];
bba = p[p[p[inc(xi)]+inc(yi)]+ zi ];
bab = p[p[p[inc(xi)]+ yi ]+inc(zi)];
bbb = p[p[p[inc(xi)]+inc(yi)]+inc(zi)];
float x1, x2, y1, y2;
x1 = lerp( grad (aaa, xf , yf , zf),
grad (baa, xf-1, yf , zf),
u);
x2 = lerp( grad (aba, xf , yf-1, zf),
grad (bba, xf-1, yf-1, zf),
u);
y1 = lerp(x1, x2, v);
x1 = lerp( grad (aab, xf , yf , zf-1),
grad (bab, xf-1, yf , zf-1),
u);
x2 = lerp( grad (abb, xf , yf-1, zf-1),
grad (bbb, xf-1, yf-1, zf-1),
u);
y2 = lerp (x1, x2, v);
return lerp (y1, y2, w);
}
这段代码是3维的perlin函数,控制参数也可以实现1维、2维计算,从perlin函数看起:
1.静态的p[512]数组散落随机数数组每256个分为一块,共两块(为了方便计算)。aaa = p[p[p[ xi ]+ yi ]+ zi ] 类似的其实就是进行一次哈希计算,打乱顺序结果尽可能随机,类似于一维中的每隔单位距离散落随机数。
2.grads数组和grad函数就是确定这个p点分别受这8个顶点影响的程度,在计算上体现就是进行内积(投影),注意这里的类比于一维的计算是有差别的:这里提到所谓的“梯度”,在一维计算里梯度就是指y = kx + 1中的k也就是斜率,而在三维空间中,梯度受3个维度的影响,在这里进行了简化从预设的12个向量中选取(至于为什么见参考链接:柏林噪声作者论文)。
3.接着就是进行lerp插值,对各个顶点方向上的计算结果进行平滑。
float rand(float2 p){
return frac(sin(dot(p ,float2(12.9898,78.233))) * 43758.5453);
}
float noise(float2 x)
{
float2 i = floor(x);
float2 f = frac(x);
float a = rand(i);
float b = rand(i + float2(1.0, 0.0));
float c = rand(i + float2(0.0, 1.0));
float d = rand(i + float2(1.0, 1.0));
float2 u = f * f * f * (f * (f * 6 - 15) + 10);
float x1 = lerp(a,b,u.x);
float x2 = lerp(c,d,u.x);
return lerp(x1,x2,u.y);
}
可以看到这种实现和上文中的思路是一样的,只是hash函数和计算各个方向上的影响计算进行了简化。
可以看出柏林函数的输出具有“波”的特点,那么自然可以所有对于波的操作。
进行类似正弦波调幅、调频、调相,还可以上下偏移
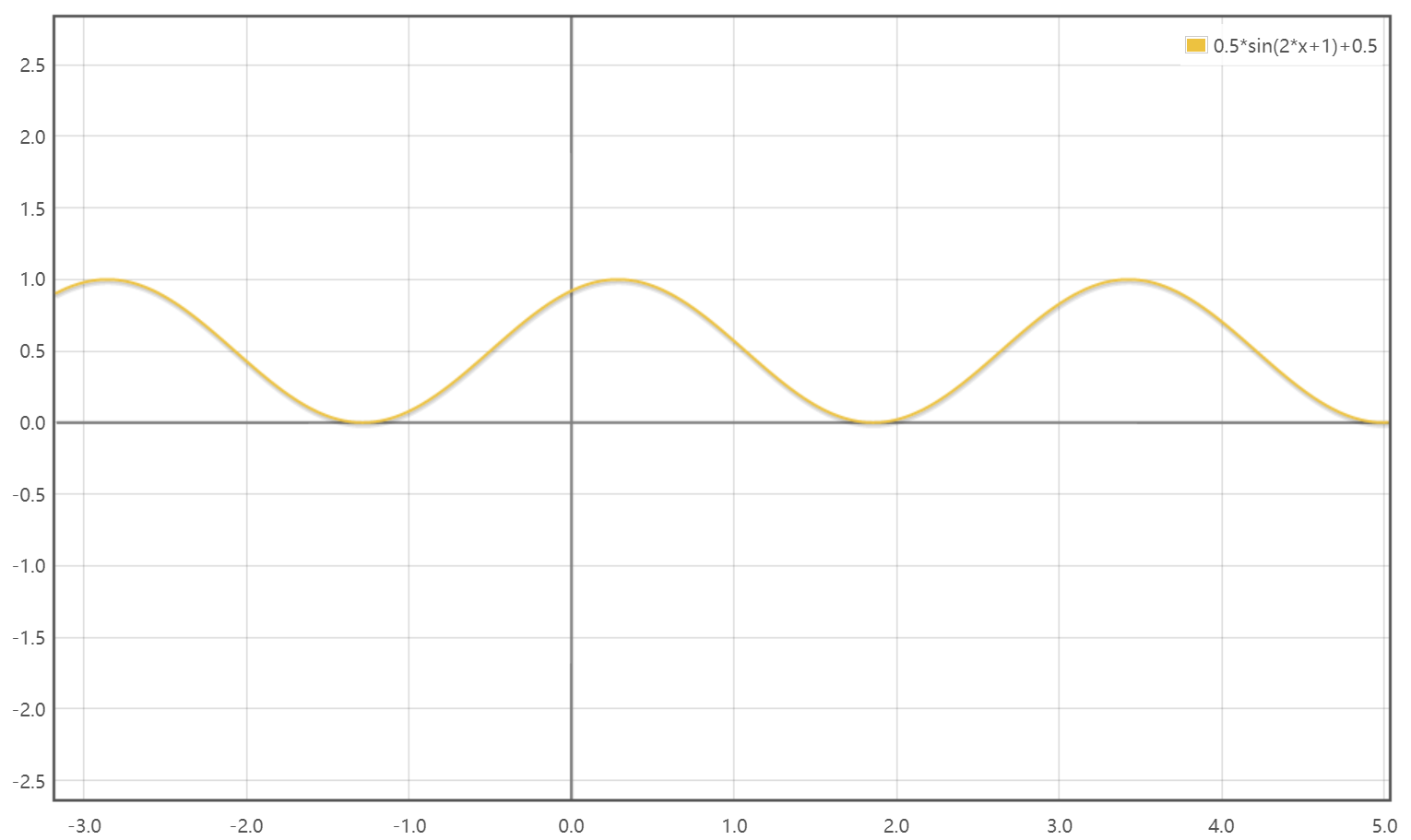
(f(x)=Asin(ωx+φ) + b 这里 A = 0.5, w = 2, φ = 1, b = 0.5)
波的叠加
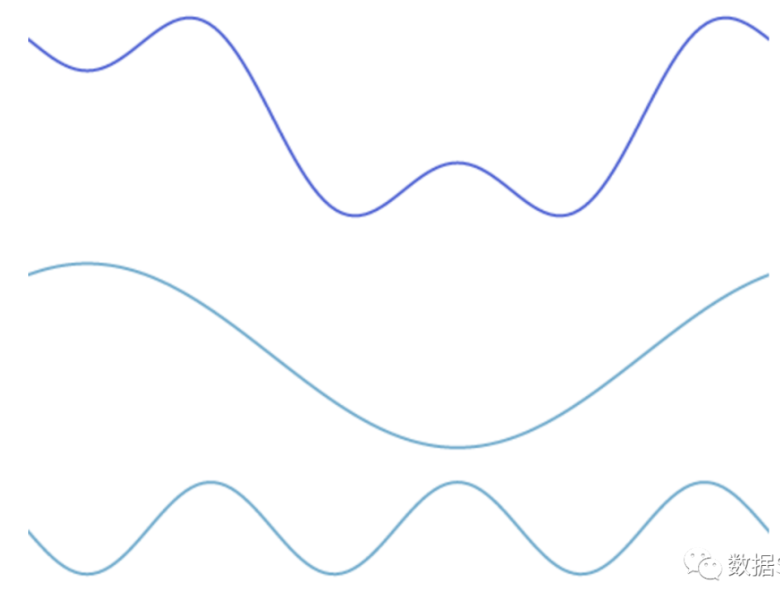
傅里叶变换说一个波可以由为n个波叠加而成,叠加结果如图所示。
波形的调整在实际应用中作用很大,如:
以上就是基于c++实现柏林噪声算法(Perlin Noise)的详细内容,更多关于C++柏林噪声算法的资料请关注编程网其它相关文章!
--结束END--
本文标题: 基于C++实现柏林噪声算法(Perlin Noise)
本文链接: https://lsjlt.com/news/202728.html(转载时请注明来源链接)
有问题或投稿请发送至: 邮箱/279061341@qq.com QQ/279061341
2024-03-01
2024-03-01
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
回答
回答
回答
回答
回答
回答
回答
回答
回答
回答
0