用Python实现数据结构之树

树是由根结点和若干颗子树构成的。树是由一个集合以及在该集合上定义的一种关系构成的。集合中的元素称为树的结点，所定义的关系称为父子关系。父子关系在树的结点之间建立了一个层次结构。在这种层次结构中有一个结点具有特殊的地位，这个结点称为该树的根结点，或称为树根。

• 根节点：树中最顶部的元素

• 父节点：处了根节点都有父节点，每个节点最多只有一个父节点

• 孩子节点：一个父节点具有0个或多个孩子节点

• 兄弟节点：同一个父节点的孩子节点之间是兄弟关系

• 外部节点：一个没有孩子的节点称为外部节点，也叫叶子结点

• 内部节点：有一个或多个孩子节点的节点叫做内部节点

• 树的边：指一对节点(u,v)，其中u是v的父节点或者v是u的父节点

• 树的路径：一系列连续的边组成了一条路径

• 节点的深度：节点的深度就是该节点的祖先的个数，不包括该节点本身，如果根节点的层数为1，则深度即为该节点的层数-1

• 节点的高度：如果p是树中的叶子节点，那么它的高度为0.否则p的高度是它的孩子节点中的最大高度+1

• 有序树：每个孩子之间有一定的顺序，例如：

class Tree():
    """
    树的抽象基类
    """

    # 叫做位置的内嵌类，用于封装节点
    class Position():

        def element(self):
            raise NotImplementedError('must be implemented by subclass')

        def __eq__(self, other):
            raise NotImplementedError('must be implemented by subclass')

    def root(self):
        """
        return 根节点的position
        """
        raise NotImplementedError('must be implemented by subclass')

    def parent(self,p):
        """

        :param p:一个位置对象
        :return: 返回p的父节点的position对象，如果p是根节点则饭后空
        """
        raise NotImplementedError('must be implemented by subclass')

    def num_children(self,p):
        """

        :param p:一个位置对象
        :return: 返回该位置的孩子节点的数量
        """
        raise NotImplementedError('must be implemented by subclass')

    def children(self,p):
        """

        :param p: 一个位置对象
        :return: 返回位置p的孩子的迭代
        """
        raise NotImplementedError('must be implemented by subclass')

    def __len__(self):
        """

        :return: 返回整个树的节点个数
        """

　　　　　raise NotImplementedError('must be implemented by subclass')

    def is_root(self,p):
        return self.root() == p

    def is_leaf(self,p):
        return self.num_children(p) == 0

    def is_empty(self):
        return len(self) == 0

这个抽象类中的方法必须在子类中实现才能调用，不然会产生NotImplementedError(‘must be implemented by subclass’)的异常

除此之外，对于Position()这个内嵌类可能较难理解，为什么要有这么一个内嵌类

这个内嵌类目前也是抽象类，具体方法都没有实现，但使用它的目的已经有了，就是将树中的节点进行封装，那为什么要封装节点呢？当调用树的相关方法时，节点可能为一个必要的参数，但我们手动传入时，实际上可以是任意的对象，这就会导致错误发生，所以我们必须保证传入的节点是节点的对象，同时也是本树对象的节点，不然就会弄混树与树的节点。同时将节点进行封装，可以避免使用者直接使用节点对象本身，相关节点的方法可以在封装成的Position对象调用。目前只是抽象类的定义，节点类等其他方法还未定义，后面还会看到具体的position对象的使用。

目前有了Tree这个抽象类，虽然其中的大多数方法还是抽象方法，但使用这些方法已经可以构成一些其他的功能了，所以就有了is_root，is_leaf，is_empty方法的定义。同时还可以定义计算节点的深度与高度的方法：

def depth(self,p):
    """
    计算节点在树中的深度
    """
    if self.is_root(p):
        return 0
    else:
        return 1 + self.depth(self.parent(p))

def height(self,p):
    """
    计算节点在树中的深度 
    """
    if self.is_leaf(p):
        return 0
    else:
        return 1 + max(self.height(c) for c in self.children(p))

我们现在介绍一种树的特殊化形式二叉树

二叉树的特点：

• 每个父节点最多只有两个孩子节点

• 两个孩子节点又叫做左孩子和右孩子

• 以左孩子为根节点形成的树叫做左子树，以右孩子为根节点形成的树叫做右子树

• 如果除了最下面的一层节点，其余节点组成的是一颗满二叉树，并且最下面的这层节点遵循从左到右依次添加的顺序，那么这个树就叫做完全二叉树

• 非空完全二叉树中，外部节点数=内部节点数+1

二叉树的实现可以以继承树的抽象类的方式实现：

class BinaryTree(Tree):

    class node():

        def __init__(self, element, parent=None, left=None, right=None):
            self.element = element
            self.parent = parent
            self.left = left
            self.right = right

    class Position(Tree.Position):

        def __init__(self, container, node):
            self.container = container
            self.node = node

        def element(self):
            return self.node.element

        def __eq__(self, other):
            return isinstance(other, type(self)) and other.node is self.node

    def validate(self, p):
        """
        进行位置验证
        """
        if not isinstance(p, self.Position):
            raise TypeError('p must be proper Position type')
        if p.container is not self:
            raise ValueError('p does not belong to this container')
        if p.node.parent is p.node:
            raise ValueError('p is no longer valid')
        return p.node

    def make_position(self, node):
        """
        封装节点
        """
        return self.Position(self, node) if node is not None else None

    def __init__(self):
        self._root = None
        self.size = 0

    def __len__(self):
        return self.size

    def root(self):
        return self.make_position(self._root)

    def parent(self, p):
        node = self.validate(p)
        return self.make_position(node.parent)

    def left(self, p):
        node = self.validate(p)
        return self.make_position(node.left)

    def right(self, p):
        node = self.validate(p)
        return self.make_position(node.right)

    def sibling(self, p):
        parent = self.parent(p)
        if parent is None:
            return None
        else:
            if p == self.left(parent):
                return self.right(parent)
            else:
                return self.left(parent)

    def num_children(self, p):
        node = self.validate(p)
        count = 0
        if node.left is not None:
            count += 1
        if node.right is not None:
            count += 1
        return count
　　

    def children(self,p):
        if self.left(p) is not None:
            yield self.left(p)
        if self.right(p) is not None:
            yield self.right(p)

代码中将之前的抽象方法进行了完整的定义，同时添加了validate与make_position方法。validate方法用于对传入的position参数进行验证，make_position方法用于将节点进行封装。除此之外还添加了二叉树特有的方法right，left和sibling，left与right分别返回节点的左孩子节点与右孩子节点，sibling返回的是节点的兄弟节点。

目前的二叉树的数据结构只是创建了一颗空树，我们接下来要加入的是对二叉树进行更新操作的方法

def add_root(self, e):
    if self._root is not None:
        raise ValueError('Root exists')
    self.size += 1
    self._root = self.Node(e)
    return self.make_position(self._root)

def add_left(self, e, p):
    node = self.validate(p)
    if node.left is not None:
        raise ValueError('Left child exists')
    self.size += 1
    node.left = self.Node(e, node)
    return self.make_position(node.left)

def add_right(self, e, p):
    node = self.validate(p)
    if node.right is not None:
        raise ValueError('Left child exists')
    self.size += 1
    node.right = self.Node(e, node)
    return self.make_position(node.right)

def replace(self, p, e):
    node = self.validate(p)
    old = node.element
    node.element = e
    return old

def delete(self, p):
    """
    删除该位置的节点，如果该节点有两个孩子，则会产生异常，如果只有一个孩子，
    则使其孩子代替该节点与其双亲节点连接
    """
    node = self.validate(p)
    if self.num_children(p) == 2:
        raise ValueError('p has two children')
    child = node.left if node.left else node.right
    if child is not None:
        child.parent = node.parent
    if node is self._root:
        self._root = child
    else:
        parent = node.parent
        if node is parent.left:
            parent.left = child
        else:
            parent.right = child
    self.size -= 1
    node.parent = node
    return node.element

总共加入了添加根节点，添加左孩子，添加右孩子，代替元素和删除节点5个方法，其中删除几点稍微有一些复杂，因为涉及到许多情况的判断。

到现在，一个完整的二叉树数据结构基本完成了。

但是我们还需要掌握一个算法，就是树的遍历算法

树的遍历一般有先序遍历，后序遍历，广度优先遍历（层序遍历），对于二叉树还有中序遍历

先序遍历

先序遍历是按照根节点->从左到右的孩子节点的顺序遍历，而且把每个孩子节点看作是子树的根节点同样如此，例如：

用python实现先序遍历为：

def preorder(self,p):
    """
    先序遍历节点p为根节点的树
    """
    yield p
    for c in self.children(p):
        for other in self.preorder(c):
            yield other

虽然代码只有4行，但理解起来却不是很容易的，首先该方法是一个生成器，所以通过yield返回一个可迭代对象，也就是可以for循环该方法，由于是先序遍历，所以要先yield p，之后便要返回孩子节点，由于孩子节点可能还具有孩子，所以并不能只返回孩子节点，应该返回以孩子节点为根节点的树的所有节点，而要想for循环得到左右的孩子节点为根节点的所有节点，还需要调用孩子节点的先序遍历方法才能得到。总而言之，代码理解的难度还是由于递归算法造成的，一个复杂的递归终归还是不是那么容易就能看出来的。

后序遍历

后序遍历是按照先从左到右孩子节点->根节点，如图：

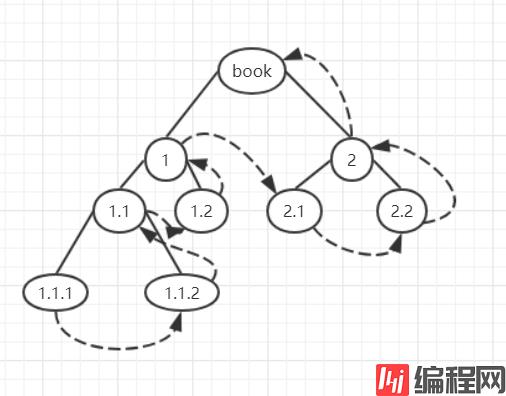
用Python实现：

def postorder(self,p):
    """
    后序遍历节点p为根的树 
    """
    for c in self.children(p):
        for other in self.postorder(c):
            yield other
    yield p

理解与先序遍历相同

广度优先遍历

广度优先遍历也叫层序遍历，一层一层的遍历，如图：

用python实现：

def breadthfirst(self):
    if not self.is_empty():
        queue = Queue()
        queue.enqueue(self.root())
        while not queue.is_empty():
            p = queue.dequeue()
            yield p
            for i in self.children(p):
                queue.enqueue(i)

中序遍历二叉树

对于二叉树，遍历顺序为左孩子->父节点->右孩子

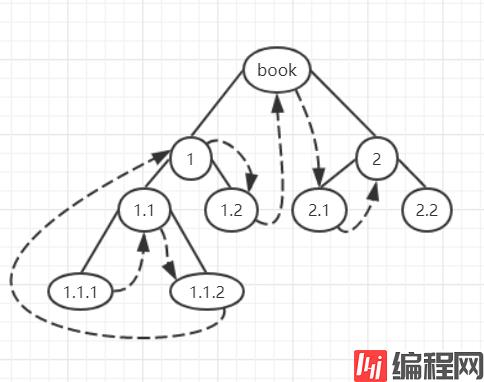
python实现为：

def inorder(self,p):
    if self.left(p) is not None:
        for other in self.inorder(self.left(p)):
            yield other
    if self.right(p) is not None:
        for other in self.inorder(self.right(p)):
            yield other

---

参考《数据结构与算法Python语言实现》

​