C#实现FFT(递归法)的示例代码

2024-04-02 19:04:59 225人浏览泡泡鱼

摘要

目录1. C#实现复数类2. 递归法实现FFT3. 补充：窗函数1. C#实现复数类我们在进行信号分析的时候，难免会使用到复数。但是遗憾的是，C#没有自带的复数类，以下提供了一种复

1. C#实现复数类

我们在进行信号分析的时候，难免会使用到复数。但是遗憾的是，C#没有自带的复数类，以下提供了一种复数类的构建方法。

复数相比于实数，可以理解为一个二维数，构建复数类，我们需要实现以下这些内容：

复数实部与虚部的属性
复数与复数的加减乘除运算
复数与实数的加减乘除运算
复数取模
复数取相位角
欧拉公式（即e^ix+y）

C#实现的代码如下：

 public class Complex
    {
        double real;
        double imag;
        public Complex(double x, double y)   //构造函数
        {
            this.real = x;
            this.imag = y;
        }
        //通过属性实现对复数实部与虚部的单独查看和设置
        public double Real
        {
            set { this.real = value; }
            get { return this.real; }
        }
        public double Imag
        {
            set { this.imag = value; }
            get { return this.imag; }
        }
        //重载加法
        public static Complex operator +(Complex c1, Complex c2)
        {
            return new Complex(c1.real + c2.real, c1.imag + c2.imag);
        }
        public static Complex operator +(double c1, Complex c2)
        {
            return new Complex(c1 + c2.real, c2.imag);
        }
        public static Complex operator +(Complex c1, double c2)
        {
            return new Complex(c1.Real + c2, c1.imag);
        }
        //重载减法
        public static Complex operator -(Complex c1, Complex c2)
        {
            return new Complex(c1.real - c2.real, c1.imag - c2.imag);
        }
        public static Complex operator -(double c1, Complex c2)
        {
            return new Complex(c1 - c2.real, -c2.imag);
        }
        public static Complex operator -(Complex c1, double c2)
        {
            return new Complex(c1.real - c2, c1.imag);
        }
        //重载乘法
        public static Complex operator *(Complex c1, Complex c2)
        {
            double cr = c1.real * c2.real - c1.imag * c2.imag;
            double ci = c1.imag * c2.real + c2.imag * c1.real;
            return new Complex(Math.Round(cr, 4), Math.Round(ci, 4));
        }
        public static Complex operator *(double c1, Complex c2)
        {
            double cr = c1 * c2.real;
            double ci = c1 * c2.imag;
            return new Complex(Math.Round(cr, 4), Math.Round(ci, 4));
        }
        public static Complex operator *(Complex c1, double c2)
        {
            double cr = c1.Real * c2;
            double ci = c1.Imag * c2;
            return new Complex(Math.Round(cr, 4), Math.Round(ci, 4));
        }

        //重载除法
        public static Complex operator /(Complex c1, Complex c2)
        {
            if (c2.real == 0 && c2.imag == 0)
            {
                return new Complex(double.NaN, double.NaN);
            }
            else
            {
                double cr = (c1.imag * c2.imag + c2.real * c1.real) / (c2.imag * c2.imag + c2.real * c2.real);
                double ci = (c1.imag * c2.real - c2.imag * c1.real) / (c2.imag * c2.imag + c2.real * c2.real);
                return new Complex(Math.Round(cr, 4), Math.Round(ci, 4));           //保留四位小数后输出
            }
        }
      
        public static Complex operator /(double c1, Complex c2)
        {
            if (c2.real == 0 && c2.imag == 0)
            {
                return new Complex(double.NaN, double.NaN);
            }
            else
            {
                double cr = c1 * c2.Real / (c2.imag * c2.imag + c2.real * c2.real);
                double ci = -c1 * c2.imag / (c2.imag * c2.imag + c2.real * c2.real);
                return new Complex(Math.Round(cr, 4), Math.Round(ci, 4));           //保留四位小数后输出
            }
        }
      
        public static Complex operator /(Complex c1, double c2)
        {
            if (c2 == 0)
            {
                return new Complex(double.NaN, double.NaN);
            }
            else
            {
                double cr = c1.Real / c2;
                double ci = c1.imag / c2;
                return new Complex(Math.Round(cr, 4), Math.Round(ci, 4));           //保留四位小数后输出
            }
        }
        //创建一个取模的方法
        public static double Abs(Complex c)
        {
            return Math.Sqrt(c.imag * c.imag + c.real * c.real);
        }
        //创建一个取相位角的方法
        public static double Angle(Complex c)
        {
            return Math.Round(Math.Atan2(c.real, c.imag), 6);//保留6位小数输出
        }
        //重载字符串转换方法,便于显示复数
        public override string ToString()
        {
            if (imag >= 0)
                return string.FORMat("{0}+i{1}", real, imag);
            else
                return string.Format("{0}-i{1}", real, -imag);
        }
        //欧拉公式
        public static Complex Exp(Complex c)
        {
            double amplitude = Math.Exp(c.real);
            double cr = amplitude * Math.Cos(c.imag);
            double ci = amplitude * Math.Sin(c.imag);
            return new Complex(Math.Round(cr, 4), Math.Round(ci, 4));//保留四位小数输出
        }
    }

2. 递归法实现FFT

以下的递归法是基于奇偶分解实现的。

奇偶分解的原理推导如下：

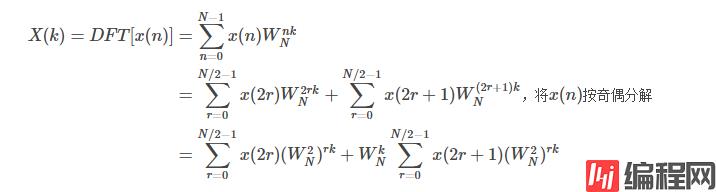
x(2r)和x(2r+1)都是长度为N/2−1的数据序列，不妨令

则原来的DFT就变成了：

于是，将原来的N点傅里叶变换变成了两个N/2点傅里叶变换的线性组合。

但是，N/2点傅里叶变换只能确定N/2个频域数据，另外N/2个数据怎么确定呢？

因为X₁(k)和X₂(k)周期都是N/2，所以有

从而得到：

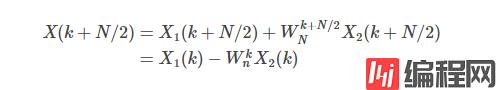
综上，我们就可以得到递归法实现FFT的流程：

1.对于每组数据，按奇偶分解成两组数据

2.两组数据分别进行傅里叶变换，得到X₁(k)和X₂(k)

3.总体数据的X(k)由下式确定：

4.对上述过程进行递归

具体代码实现如下：

public Complex[] FFTre(Complex[] c)
{
    int n = c.Length;
    Complex[] cout = new Complex[n];
    if (n == 1)
    {
        cout[0] = c[0];
        return cout;
    }
    else
    {
        double n_2_f = n / 2;
        int n_2 = (int)Math.Floor(n_2_f);
        Complex[] c1 = new Complex[n / 2];
        Complex[] c2 = new Complex[n / 2];
        for (int i = 0; i < n_2; i++)
        {
            c1[i] = c[2 * i];
            c2[i] = c[2 * i + 1];
        }
        Complex[] c1out = FFTre(c1);
        Complex[] c2out = FFTre(c2);
        Complex[] c3 = new Complex[n / 2];
        for (int i = 0; i < n / 2; i++)
        {
            c3[i] = new Complex(0, -2 * Math.PI * i / n);
        }
        for (int i = 0; i < n / 2; i++)
        {
            c2out[i] = c2out[i] * Complex.Exp(c3[i]);
        }

        for (int i = 0; i < n / 2; i++)
        {
            cout[i] = c1out[i] + c2out[i];
            cout[i + n / 2] = c1out[i] - c2out[i];
        }
        return cout;
    }
}

3. 补充：窗函数

顺便提供几个常用的窗函数：

Rectangle
Bartlett
Hamming
Hanning
Blackman

    public class WDSLib
    {
        //以下窗函数均为periodic
        public double[] Rectangle(int len)
        {
            double[] win = new double[len];
            for (int i = 0; i < len; i++)
            {
                win[i] = 1;
            }
            return win;
        }

        public double[] Bartlett(int len)
        {
            double length = (double)len - 1;
            double[] win = new double[len];
            for (int i = 0; i < len; i++)
            {
                if (i < len / 2) { win[i] = 2 * i / length; }
                else { win[i] = 2 - 2 * i / length; }
            }
            return win;
        }

        public double[] Hamming(int len)
        {
            double[] win = new double[len];
            for (int i = 0; i < len; i++)
            {
                win[i] = 0.54 - 0.46 * Math.Cos(Math.PI * 2 * i / len);
            }
            return win;
        }

        public double[] Hanning(int len)
        {
            double[] win = new double[len];
            for (int i = 0; i < len; i++)
            {
                win[i] = 0.5 * (1 - Math.Cos(2 * Math.PI * i / len));
            }
            return win;
        }

        public double[] Blackman(int len)
        {
            double[] win = new double[len];
            for (int i = 0; i < len; i++)
            {
                win[i] = 0.42 - 0.5 * Math.Cos(Math.PI * 2 * (double)i / len) + 0.08 * Math.Cos(Math.PI * 4 * (double)i / len);
            }
            return win;
        }
    }

以上就是C#实现FFT(递归法)的示例代码的详细内容，更多关于C# FFT递归法的资料请关注编程网其它相关文章！

--结束END--

本文标题: C#实现FFT(递归法)的示例代码

本文链接: https://lsjlt.com/news/154100.html(转载时请注明来源链接)

有问题或投稿请发送至: 邮箱/279061341@qq.com QQ/279061341