扫码关注官方微信

扫码下载APP
返回顶部
首页 > 资讯 > 后端开发 > 其他教程 >基于Matlab制作一个数独求解器
  • 887

0
分享到

基于Matlab制作一个数独求解器

2024-04-02 19:04:59 887人浏览 薄情痞子
摘要

目录1.完整效果2.数独求解(错误示范)3.数独求解(升维)4.数字识别5.GUI / APP讲解一个完整的小项目，顺便说明如何使用整数规划求解数独。 1.完整效果 2.数独求解

讲解一个完整的小项目，顺便说明如何使用整数规划求解数独。

1.完整效果

2.数独求解(错误示范)

首先我们先尝试如果只满足行、列、3x3块加和均为45的等式约束是否有效。即约束为：

每行和为45:

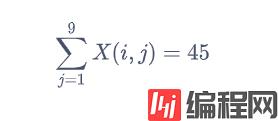
每列和为45:

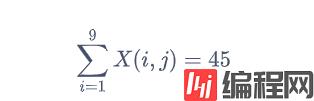
每个3x3块和为45:

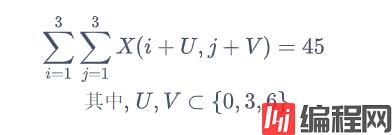
其中对此编写如下代码：

sudokuMat=[1 0 5 0 2 0 0 0 0
     0 0 0 7 4 3 0 0 5
     3 0 7 0 0 0 0 0 9
     0 2 0 0 0 0 4 5 0
     0 6 0 4 0 1 0 8 0
     0 7 4 0 0 0 0 6 0
     2 0 0 0 0 0 3 0 8
     4 0 0 8 5 6 0 0 0
     0 0 0 0 3 0 5 0 6];
% 记录原本各个数字所在位置，构造等式约束
n0Ind=find(sudokuMat~=0); 
Aeq1=zeros(length(n0Ind),81);
for i=1:length(n0Ind)
    Aeq1(i,n0Ind(i))=1;
end
beq1=sudokuMat(sudokuMat~=0);

% 行等式约束和列等式约束
Aeq2=zeros(9,81);
Aeq3=zeros(9,81);
for i=1:9
    Aeq2(i,(i-1)*9+1:i*9)=1;
    Aeq3(i,i:9:81)=1;
end
beq2=ones(9,1).*45;
beq3=ones(9,1).*45;

% 3x3块等式约束
Aeq4=zeros(9,81);
for i=1:3
    for j=1:3
        tmat=zeros(9,9);
        tmat((i-1)*3+1:i*3,(j-1)*3+1:j*3)=1;
        Aeq4((i-1)*3+j,:)=tmat(:)';
    end
end
beq4=ones(9,1).*45;

f=ones(1,81);    % 不重要，随便设置
intcon=1:81;     % 所有元素都要求为整数
lb=ones(81,1);   % 下限为1
ub=ones(81,1).*9;% 上限为1
Aeq=[Aeq1;Aeq2;Aeq3;Aeq4];
beq=[beq1;beq2;beq3;beq4];
% 求解整数规划
X=intlinprog(f,intcon,[],[],Aeq,beq,lb,ub);
% 重新 构造数独矩阵
X=reshape(X,[9,9])

那么，这么简单就能够解决数独了嘛？？？

当然不行。。。。

上述程序运行结果为：

1 8 5 6 2 9 9 1 4
2 9 9 7 4 3 5 1 5
3 1 7 1 4 9 8 3 9
7 2 1 8 9 4 4 5 5
9 6 1 4 1 1 9 8 6
8 7 4 1 8 9 1 6 1
2 1 9 1 9 3 3 9 8
4 9 8 8 5 6 1 3 1
9 2 1 9 3 1 5 9 6

可以发现我们的约束确实保证了三种加和都是45，但是不能保证同行、同列、同3x3块内不出现同样的数字，那咋办，总不能一个元素一个元素添加不相等信息吧、我们怎样能让矩阵包含更多的信息，更方便的阐述各个元素之间的联系呢？

3.数独求解(升维)

欸，我们原本是9x9大小的矩阵，要描述每个元素和同一行各个元素、和同一列各个元素之间的联系，一个很自然的想法就是升维！

将9×9的数独矩阵转化为9×9×9的三维矩阵(张量),此时X(i,j,k)=1意味原矩阵第i行，第j列的元素为k，整个整数规划从现在开始变成了0-1规划，要想同一行的数值都不一样，只需要所有的行纤维的和都是1，想要同一列的数值都不一样，只需要所有列纤维的和都是1，非常奇妙的，我们又把问题转换为了一个线性求和的问题，very amazing啊！

此时约束条件变为：

原矩阵每个小格子只能有一个数值：

原矩阵每一行的各个数字均不同：

原矩阵每一列的各个数字均不同：

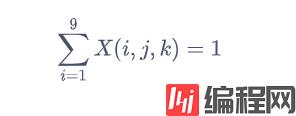
原矩阵每一个3x3块各个数字均不同：

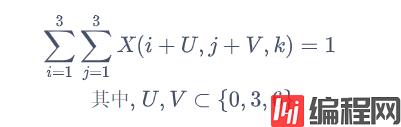
其中因此编写如下代码

sudokuMat=[1 0 5 0 2 0 0 0 0
     0 0 0 7 4 3 0 0 5
     3 0 7 0 0 0 0 0 9
     0 2 0 0 0 0 4 5 0
     0 6 0 4 0 1 0 8 0
     0 7 4 0 0 0 0 6 0
     2 0 0 0 0 0 3 0 8
     4 0 0 8 5 6 0 0 0
     0 0 0 0 3 0 5 0 6];

% 记录原本1所在位置，构造等式约束
n0Ind=find(sudokuMat~=0); 
Aeq0=zeros(length(n0Ind),9^3);
for i=1:length(n0Ind)
    Aeq0(i,n0Ind(i)+(sudokuMat(n0Ind(i))-1)*81)=1;
end

% 每一行、列、管都只能有一个1
Aeq1=zeros(81,9^3);
Aeq2=zeros(81,9^3);
Aeq3=zeros(81,9^3);
for i=1:9
    for j=1:9
        A1=zeros(9,9,9);
        A2=zeros(9,9,9);
        A3=zeros(9,9,9);
        A1(:,i,j)=1;Aeq1((i-1)*9+j,:)=A1(:)';
        A2(i,:,j)=1;Aeq2((i-1)*9+j,:)=A2(:)';
        A3(i,j,:)=1;Aeq3((i-1)*9+j,:)=A3(:)';
    end
end

% 每个3x3的小矩阵都只能有一个1
Aeq4=zeros(81,9^3);
for k=1:9
    for i=1:3
        for j=1:3
            A4=zeros(9,9,9);
            A4((i-1)*3+1:i*3,(j-1)*3+1:j*3,k)=1;
            Aeq4((k-1)*9+(i-1)*3+j,:)=A4(:)';
        end
    end
end

f=ones(1,9^3);  % 不重要，随便设置
intcon=1:9^3;   % 所有元素都要求为整数
lb=zeros(9^3,1);% 下限为0
ub=ones(9^3,1); % 上限为1
Aeq=[Aeq0;Aeq1;Aeq2;Aeq3;Aeq4];
beq=ones(size(Aeq,1),1);
% 求解整数规划
X=intlinprog(f,intcon,[],[],Aeq,beq,lb,ub);
% 重新 构造数独矩阵
X=reshape(X,[9,9,9]);
resultMat=zeros(9,9);
for i=1:9
    resultMat=resultMat+X(:,:,i).*i;
end
resultMat

求解结果为：

LP:Optimal objective value is 81.000000.

Optimal solution found.

Intlinprog stopped at the root node because the objective value is within a gap tolerance of the optimal value, options.AbsoluteGapTolerance = 0 

The intcon variables are integer within tolerance, options.IntegerTolerance = 1e-05

resultMat 

1 8 5 6 2 9 7 3 4
6 9 2 7 4 3 8 1 5
3 4 7 1 8 5 6 2 9
9 2 1 3 6 8 4 5 7
5 6 3 4 7 1 9 8 2
8 7 4 5 9 2 1 6 3
2 5 6 9 1 7 3 4 8
4 3 9 8 5 6 2 7 1
7 1 8 2 3 4 5 9 6

历时 0.017170 秒，快到离谱。不得不说MATLAB规划算法还是niubility！

4.数字识别

想要做读取图片后识别数独矩阵的功能，但是本文做的只是一个基础款，没打算搞歪歪斜斜的数独题目图像，也没打算识别那些手写字体，于是既没有做角度矫正，也没搞CNN数字识别，大家学会基础款后可以自行添加相关功能，本文中的数字识别只是将图像切割后和数字库里几个图像进行对比：

只是做了简单的最小二乘法，求差值平方和，找到差异最小的图片，非常的简单，因此只能应对一些横平竖直的数独题目。

5.GUI / APP

反正都很简单，我就GUI版本和App designer版本都做了，以下仅展示 GUI 版本代码

function sudokuGui
% @author:slandarer

% GUI图窗创建
SDKFig=uifigure('units','pixels',...
    'position',[300 100 450 500],...
    'Numbertitle','off',...
    'menubar','none',...
    'resize','off',...
    'name','数独求解器 1.0',...
    'color',[1,1,1].*0.97);
SDKFig.AutoResizeChildren='off';
SDKAxes=uiaxes('Units','pixels',...
      'parent',SDKFig,...
      'PlotBoxAspectRatio',[1 1 1],...
      'Position',[15 15 420 420],...
      'Color',[0.99 0.99 0.99],... 
      'Box','on', ...
      'XLim',[0 1],'YLim',[0 1],...
      'XTick',[],'YTick',[]);
hold(SDKAxes,'on');
% SDKAxes.Toolbar.Visible='off';
% 按钮创建
uibutton(SDKFig,'Text','导  入  图  片','BackgroundColor',[0.31 0.58 0.80],'FontColor',[1 1 1],...
    'FontWeight','bold','Position',[25,450,150,35],'FontSize',13,'ButtonPushedFcn',@loadPic);  
uibutton(SDKFig,'Text','开  始  计  算','BackgroundColor',[0.31 0.58 0.80],'FontColor',[1 1 1],...
    'FontWeight','bold','Position',[200,450,150,35],'FontSize',13,'ButtonPushedFcn',@solveSDK); 
% =========================================================================
% 读取图像库内图像
path='数字图像库';
picInfor=dir(fullfile(path,'*.jpg'));
SDKPicSet{size(picInfor,1)}=[];
for n=1:size(picInfor,1)
    tempPic=imread([path,'\',picInfor(n).name]);
    SDKPicSet(n)={tempPic};
end
oriPic=[];

    % 图像读取函数
    function loadPic(~,~)
        try
            [filename, pathname] = uigetfile({'*.jpg;*.tif;*.png;*.gif','All Image Files';...
                '*.*','All Files' });
            oriPic=imread([pathname,filename]);
            Lim=max(size(oriPic));
            SDKAxes.XLim=[0 Lim];
            SDKAxes.YLim=[0 Lim];
            imshow(oriPic,'parent',SDKAxes)
        catch
        end
    end

    % 数独求解函数
    function solveSDK(~,~)
        % 提取数独矩阵及数独矩阵在图片中位置
        [XLim,YLim,sudokuMat]=getMat(oriPic);
        
        % 整数规划求解数独
        resultMat=sudoku(sudokuMat);disp(resultMat)

        % 补全数独图像
        fillSDK(XLim,YLim,resultMat,sudokuMat)
    end


% =========================================================================
    % 提取数独矩阵
    function [XLim,YLim,sudokuMat]=getMat(oriPic)
        bw=~im2bw(oriPic);
        deletedRange=round(((size(bw,1)+size(bw,2))/2)^2*0.00005);
        bw=bwareaopen(bw,deletedRange);
        % 定位数独表格
        xDistrib=find(sum(bw,2)~=0);
        yDistrib=find(sum(bw,1)~=0);
        XLim=[xDistrib(1),xDistrib(end)];
        YLim=[yDistrib(1),yDistrib(end)];
        % 将图像进行切割并将数字填入矩阵
        numPicSize=[round((XLim(2)-XLim(1)+1)/9),round((YLim(2)-YLim(1)+1)/9)];
        selectedPic=imresize(bw(XLim(1):XLim(2),YLim(1):YLim(2)),9.*numPicSize);
        sudokuMat=zeros(9,9);
        for i=1:9
            for j=1:9
                % 切割出每个数字
                numPic=selectedPic((i-1)*numPicSize(1)+1:i*numPicSize(1),(j-1)*numPicSize(2)+1:j*numPicSize(2));
                numPic=imclearborder(numPic);
                xDistrib=find(sum(numPic,2)~=0);
                yDistrib=find(sum(numPic,1)~=0);
                if ~any(xDistrib)||~any(yDistrib)% 若是方框是空的设置矩阵数值为0
                    sudokuMat(i,j)=0;
                else
                    xLim=[xDistrib(1),xDistrib(end)];
                    yLim=[yDistrib(1),yDistrib(end)];
                    % 为了区分1和7,这里多删去一块
                    numPic=numPic(xLim(1):xLim(2)-round(0.1*(xLim(2)-xLim(1))),yLim(1):yLim(2));
                    xDistrib=find(sum(numPic,2)~=0);
                    yDistrib=find(sum(numPic,1)~=0);
                    xLim=[xDistrib(1),xDistrib(end)];
                    yLim=[yDistrib(1),yDistrib(end)];
                    numPic=numPic(xLim(1):xLim(2),yLim(1):yLim(2));
                    numPic=imresize(numPic,[70 40]);
                    % 最小二乘法选出最可能的数值
                    tempVarin=inf.*ones(1,size(picInfor,1));
                    % 循环和图像库中图像做差值并求平方和
                    for k=1:size(picInfor,1)
                        tempVarin(k)=sum((double(SDKPicSet{k})-numPic.*255).^2,[1,2]);
                    end
                    tempStr=picInfor(tempVarin==min(tempVarin)).name;
                    sudokuMat(i,j)=str2double(tempStr(1));
                end
            end
        end
    end
% -------------------------------------------------------------------------
    % 整数规划求解数独
    function resultMat=sudoku(sudokuMat)
        % 记录原本1所在位置，构造等式约束
        n0Ind=find(sudokuMat~=0);
        Aeq0=zeros(length(n0Ind),9^3);
        for i=1:length(n0Ind)
            Aeq0(i,n0Ind(i)+(sudokuMat(n0Ind(i))-1)*81)=1;
        end
        % 每一行、列、管都只能有一个1
        Aeq1=zeros(81,9^3);
        Aeq2=zeros(81,9^3);
        Aeq3=zeros(81,9^3);
        for i=1:9
            for j=1:9
                A1=zeros(9,9,9);
                A2=zeros(9,9,9);
                A3=zeros(9,9,9);
                A1(:,i,j)=1;Aeq1((i-1)*9+j,:)=A1(:)';
                A2(i,:,j)=1;Aeq2((i-1)*9+j,:)=A2(:)';
                A3(i,j,:)=1;Aeq3((i-1)*9+j,:)=A3(:)';
            end
        end
        % 每个3x3的小矩阵都只能有一个1
        Aeq4=zeros(81,9^3);
        for k=1:9
            for i=1:3
                for j=1:3
                    A4=zeros(9,9,9);
                    A4((i-1)*3+1:i*3,(j-1)*3+1:j*3,k)=1;
                    Aeq4((k-1)*9+(i-1)*3+j,:)=A4(:)';
                end
            end
        end
        f=ones(1,9^3);  % 不重要，随便设置
        intcon=1:9^3;   % 所有元素都要求为整数
        lb=zeros(9^3,1);% 下限为0
        ub=ones(9^3,1); % 上限为1
        Aeq=[Aeq0;Aeq1;Aeq2;Aeq3;Aeq4];
        beq=ones(size(Aeq,1),1);
        % 求解整数规划
        X=intlinprog(f,intcon,[],[],Aeq,beq,lb,ub);
        % 重新 构造数独矩阵
        X=reshape(X,[9,9,9]);
        resultMat=zeros(9,9);
        for i=1:9
            resultMat=resultMat+X(:,:,i).*i;
        end
    end
% -------------------------------------------------------------------------
    % 补全数独
    function fillSDK(xLim,yLim,resultMat,sudokuMat)
        for i=0:9
            plot(SDKAxes,[yLim(1),yLim(1)]+i*(yLim(2)-yLim(1))/9,[xLim(1),xLim(2)],'Color',[0.29 0.65 0.85],'lineWidth',2)
            plot(SDKAxes,[yLim(1),yLim(2)],[xLim(1),xLim(1)]+i*(xLim(2)-xLim(1))/9,'Color',[0.29 0.65 0.85],'lineWidth',2)
        end
        fontSize=18;
        if (xLim(2)-xLim(1))>0.8*size(oriPic,1)
            fontSize=36;
        end
        for i=1:9
            for j=1:9
                if (resultMat(j,i)~=0)&&(sudokuMat(j,i)==0)
                text(SDKAxes,yLim(1)+(i-1)*(yLim(2)-yLim(1))/9+(yLim(2)-yLim(1))/9/2,...
                             xLim(1)+(j-1)*(xLim(2)-xLim(1))/9+(xLim(2)-xLim(1))/9/2,...
                             num2str(resultMat(j,i)),'HorizontalAlignment','center',...
                             'Color',[0.29 0.65 0.85],'fontWeight','bold','fontSize',fontSize)
                end
            end
        end
    end
end

到此这篇关于基于Matlab制作一个数独求解器的文章就介绍到这了,更多相关Matlab数独求解器内容请搜索编程网以前的文章或继续浏览下面的相关文章希望大家以后多多支持编程网！

--结束END--

本文标题: 基于Matlab制作一个数独求解器

本文链接: https://lsjlt.com/news/149482.html(转载时请注明来源链接)

有问题或投稿请发送至: 邮箱/279061341@qq.com    QQ/279061341

猜你喜欢
  • 基于Matlab制作一个数独求解器
    目录1.完整效果2.数独求解(错误示范)3.数独求解(升维)4.数字识别5.GUI / APP讲解一个完整的小项目，顺便说明如何使用整数规划求解数独。 1.完整效果 2.数独求解...
    99+
    2024-04-02
  • 基于Matlab如何制作一个数独求解器
    这篇“基于Matlab如何制作一个数独求解器”文章的知识点大部分人都不太理解，所以小编给大家总结了以下内容，内容详细，步骤清晰，具有一定的借鉴价值，希望大家阅读完这篇文章能有所收获，下面我们一起来看看这篇“基于Matlab如何制作一个数独求...
    99+
    2023-06-30
  • 基于Matlab制作一个不良图片检测系统
    目录不良图片检测部分part.0 图片导入part.1 检查是否为肤色part.2 皮肤区域标记part.3 通过皮肤区域特点判定是否为不良图片完整代码批量处理部分不良图片检测部分 ...
    99+
    2024-04-02
  • 基于PyQt5制作一个数据图表生成器
    我的需求：手动配置X轴、Y轴、图表标题等参数自动通过Pyecharts模块生成可视化的html数据图表，并将浏览器图表展示到UI界面上。 制作出图表后的效果展示如下： 另外，生成...
    99+
    2024-04-02
  • 基于Python制作一个文本翻译器
    translate非标准库是python中可以实现对多种语言进行互相翻译的库，使用时只需要设置目标语言（比如：中文、英文）后，会自动将原始文本翻译成我们需要的目标语言。 使用pip...
    99+
    2024-04-02
  • 基于Python制作一个相册播放器
    大家好，我是小F。 对于相册播放器，大家应该都不陌生(用于浏览多张图片的一个应用)。 当然还有视频、音乐播放器，同样是用来播放多个视频、音乐文件的。 在Win10系统下，用【照片】这...
    99+
    2024-04-02
  • 基于PyQt5制作一个猜数字小游戏
    开始之前，直接来看一下实现后的效果。想自己实现或者需要源码的童鞋直接进场... 将PyQt5的相关模块直接导入即可。 from PyQt5.QtGui import * from ...
    99+
    2024-04-02
  • 基于Matlab制作一款简单的龙舟小游戏
    效果图： 没找到合适的背景就自己画了个，大家如果有更好看的可以换一下。。。 步骤 1 创建Axes及图片导入 窗口创建： Mainfig=figure('units','pixe...
    99+
    2024-04-02
  • 基于PyQt5制作一个windows通知管理器
    前几天看到一个python框架win10toast，它可以用来做windows的消息通知功能。通过设定通知的间隔时间来实现一些事件通知的功能，比如可以可以提醒一头扎进代码编写过程的我...
    99+
    2024-04-02
  • 基于PyQt5制作一个PDF文件合并器
    操作说明：选择多个PDF文件，执行完合并后会生成一个新的PDF文件，这个新的PDF文件包含所有源PDF文件的页面。 将相关的三方模块导入到代码块中... from PyQt5.Qt...
    99+
    2024-04-02
  • 基于Unity制作一个简易的计算器
    目录一、前言二、效果图及源工程三、实现1.界面搭建2.代码实现四、后记一、前言 Hello，又见面了，今天分享如何使用Unity制作计算器，难度中等，可以用来学习，或者当成其他项目的...
    99+
    2024-04-02
  • 基于PyQt5制作一个表情包下载器
    每次和朋友聊天苦于没有表情包，而别人的表情包似乎是取之不尽、用之不竭。作为一个程序员哪能甘愿认输，于是做了一个表情包下载器供大家斗图。 首先，还是介绍一下设计思路吧，和我们之前做的百...
    99+
    2024-04-02
  • 基于PyQT5制作一个二维码生成器
    个性化二维码的exe桌面应用的获取方式我放在文章最后面了，注意查收。通过执行打包后的exe应用程序可以直接运行生成个性化二维码。 开始之前先来看一下通过二维码生成器是如何生成个性化二...
    99+
    2024-04-02
  • 基于JavaScript制作一个骰子游戏
    目录知识点HTML 部分CSS 部分JavaScript 部分总结游戏可以通过这个链接进入  完整源码我已经放在GitHub上了 这节实验我们将使用 HTML、CSS 和 ...
    99+
    2024-04-02
  • 基于Python制作一个桌面宠物
    目录获取素材图片窗体设置随机展示宠物图片添加动作右键菜单今天，我们来分享一个宠物桌面小程序，全程都是通过 PyQT 来制作的，对于 Python GUI 感兴趣的朋友，千万不要错过哦...
    99+
    2022-12-08
    Python实现桌面宠物 Python桌面宠物
  • 基于JavaSwing制作一个Pong小游戏
    之前呢我们用Python的Pygame做过这个Pong游戏 这一次，我们用Java的Swing来实现类似的效果 首先我们列出本次的项目结构 这个程序分为四个部分，一个程序入口，一...
    99+
    2023-01-05
    Java Swing制作Pong游戏 Java Pong游戏 Java Swing 游戏
  • 基于Matlab制作伪3D第一视角迷宫小游戏
    目录游戏效果游戏原理说明第一代程序计算交点方法第二代程序计算交点方法距离转换为线段长度完整代码游戏效果 使用键盘上方向键↑向前移动 使用键盘左右方向键调整← ...
    99+
    2024-04-02
  • 基于Python制作一个文件解压缩工具
    经常由于各种压缩格式的不一样用到文件的解压缩时就需要下载不同的解压缩工具去处理不同的文件，以至于桌面上的压缩工具就有三四种，于是使用python做了一个包含各种常见格式的文件解压缩的...
    99+
    2024-04-02
  • 基于Python制作一个多进制转换工具
    目录前言主要步骤完整代码前言 学习资料下载链接 提取码：9d4g  进制转换计算工具含源文件 主要步骤 导入模块 import tkinter from tki...
    99+
    2024-04-02
  • 基于WPF制作一个可编程画板
    目录先上一张效果动图本次扩展的主要内容可编程模块的实现原理代码编辑模块的实现代码编辑模块的编译与测试WPF打印控制台数据动态编译模块的输入输出自动生成先上一张效果动图 同样老规矩，...
    99+
    2023-05-18
    WPF制作可编程画板 WPF可编程画板 WPF 画板
软考高级职称资格查询
热门wiki
近期文章
推荐阅读
热门问答
热门标签
编程网，编程工程师的家园，是目前国内优秀的开源技术社区之一，形成了由开源软件库、代码分享、资讯、协作翻译、讨论区和博客等几大频道内容，为IT开发者提供了一个发现、使用、并交流开源技术的平台。

  • 官方手机版

  • 微信公众号

  • 商务合作