C语言简明讲解快速排序的应用

2024-04-02 19:04:59 110人浏览八月长安

摘要

目录快速排序1.1快速排序引入1.2快速排序的基本思想1.3快速排序的排序流程1.4实例说明1.5代码实现1.6性能分析快速排序快速排序,说白了就是给基准数据找其正确索引位置的过程

快速排序

快速排序,说白了就是给基准数据找其正确索引位置的过程

1.1快速排序引入

希尔排序相当于直接插入排序的升级，他们属于插入排序类；堆排序相当于简单选择排序的升级，他们同属于选择排序类；而对于交换排序类的冒泡排序升级版本就是快速排序。

1.2快速排序的基本思想

通过一趟排序将待排记录分割成独立的两部分，其中一部分记录的关键字比另一部分记录的关键字小，则可分别对这两部分记录继续进行排序，以达到整个排序的目的。

1.3快速排序的排序流程

首先设定一个分界值，通过该分界值将数组分成左右两部分。
将大于或等于分界值的数据集中到数组右边，小于分界值的数据集中到数组的左边。此时，左边部分中各元素都小于或等于分界值，而右边部分中各元素都大于或等于分界值。
然后，左边和右边的数据可以独立排序。对于左侧的数组数据，又可以取一个分界值，将该部分数据分成左右两部分，同样在左边放置较小值，右边放置较大值。右侧的数组数据也可以做类似处理。
重复上述过程，可以看出，这是一个递归定义。通过递归将左侧部分排好序后，再递归排好右侧部分的顺序。当左、右两个部分各数据排序完成后，整个数组的排序也就完成了。

总结来说：就是分治+填数

1.4实例说明

以12、10、8、22、5、13、28、21、11我们要将它按从小到大排序排序过程：

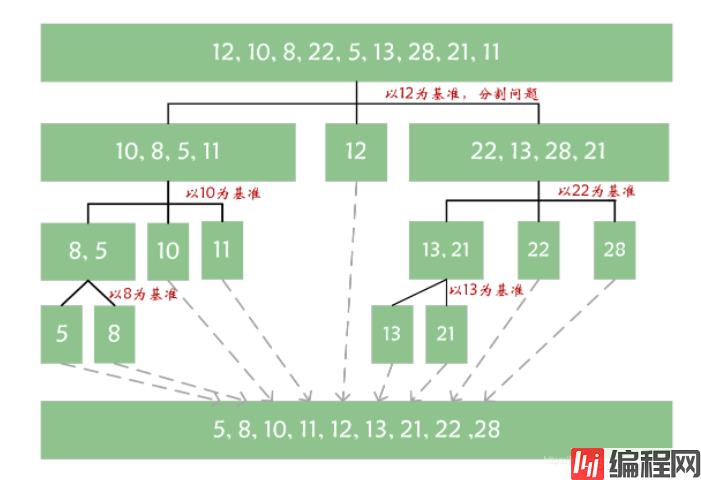
详细过程：

设定两个指针 left 和 right，它们初始分别指向待排序序列的左端和右端；此外还要附设一个基准元素 tmp（一般选取第一个，本例中基准tmp的值为 20）。

首先从 right 所指的位置从右向左搜索找到第一个小于 tmp 的元素，然后将其记录在基准元素所在的位置。

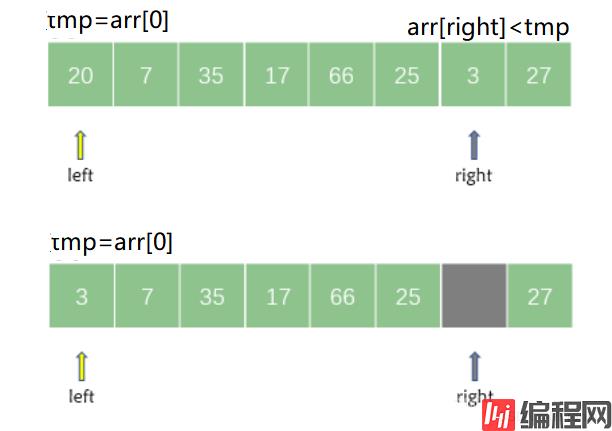
接着从 left 所指的位置从左向右搜索找到第一个大于 tmp的元素，然后将其记录在 right 所指向的位置。

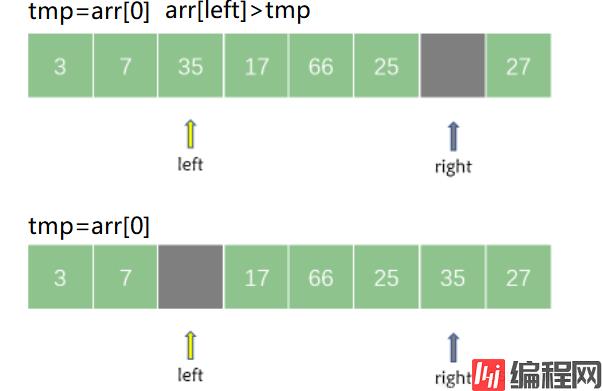
然后再从 right 所指向的位置继续从右向左搜索找到第一个小于 tmp 的元素，然后将其记录在 left 所指向的位置。

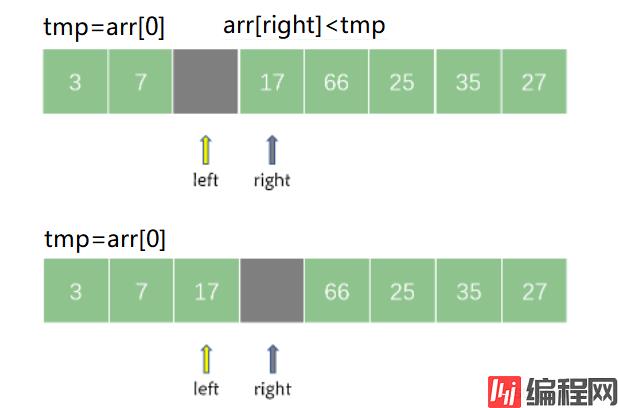
接着，left 继续从左向右搜索第一个大于 tmp的元素，如果在搜索过程中出现了 left == right ，则说明一趟快速排序结束。此时将 tmp 记录在 left 和 right 共同指向的位置即可。

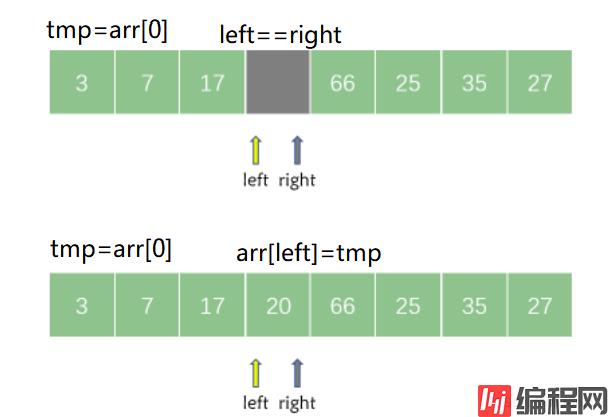
以上便是一轮快速排序的详细过程

注意：

向下划分至少需要这个组两个数据，才有必要划分，0个或者1个都没有必要
划分时：从右向左找比基准小的（相等）
从左向右找比基准值大的

1.5代码实现

//一次划分函数  核心函数  //返回基准值最终所在下标
int Partition(int *arr, int left, int right)
{
	//先讲arr数组里的[left， right]的第一个值 作为基准值
	int tmp = arr[left];
	while(left < right)
	{
		while(left<right && arr[right] > tmp)//左右边界没有相遇且当前右边的值大于基准值tmp
		right--;
		if(left < right)//如果此时，左右边界没有相遇，那就只能证明右边right找到了一个小于等于基准值tmp的值
		{
			arr[left] = arr[right];
		}
		else
		{
			break;
		}
		while(left<right && arr[left] <= tmp)//左右边界没有相遇且当前左边的值小于等于基准值tmp
		left++;
		if(left < right)//如果此时，左右边界没有相遇，那就只能证明左边left找到了一个大于基准值tmp的值
		{
			arr[right] = arr[left];
		}
		else
		{
			break;
		}
	}
	arr[left] = tmp;//此时 因为 left == right
	return left;//return right ok
}
void Quick(int *arr, int left, int right)
{
	if(left < right)//通过left <right  保证[left, right]这个范围内至少两个数据
	{
		int par = Partition(arr, left, right);
		if(left < par-1)//基准值左半部分  至少有两个值才有必要去递归
		{
			Quick(arr, left, par-1);
		}
		if(par+1 < right)//基准值右半部分  至少有两个值才有必要去递归
		{
			Quick(arr, par+1, right);
		}
	}
}
void QuickSort(int *arr, int len)
{
	Quick(arr, 0, len-1);
}