详解Java中字典树(Trie树)的图解与实现

2024-04-02 19:04:59 930人浏览安东尼

Python 官方文档：入门教程 => 点击学习

摘要

目录简介工作过程数据结构初始化构建字典树应用匹配有效单词关键词提示总结简介 Trie又称为前缀树或字典树，是一种有序树，它是一种专门用来处理串匹配的数据结构，用来解决一组字符中快速查

简介

Trie又称为前缀树或字典树，是一种有序树，它是一种专门用来处理串匹配的数据结构，用来解决一组字符中快速查找某个字符串的问题。Google搜索的关键字提示功能相信大家都不陌生，我们在输入框中进行搜索的时候，会下拉出一系列候选关键词。

上面这个关键词提示功能，底层最基本的原理就是我们今天说的数据结构：Trie树

我们先看看Tire树长什么样子，以单纯的单词匹配为例，首先它是一棵多叉树结构，根节点是一个空字符，树中节点分为普通节点和结尾节点（如图中红色节点）。结尾节点表示加上前面前缀，可以称为一个单词，如图中hi，him。

工作过程

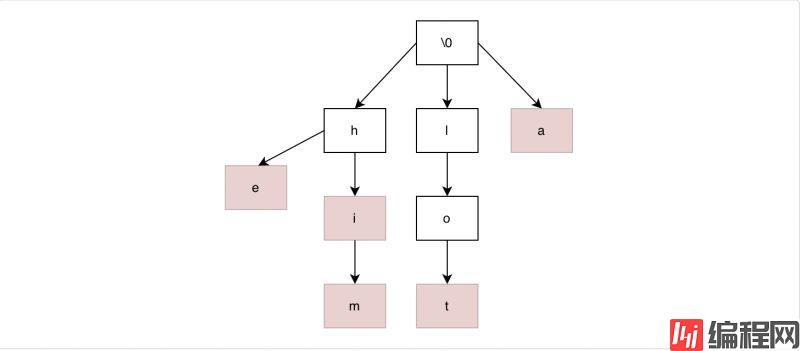
Tire树与之前串匹配最大的不同点是，之前我们都是单模式串，查看主串中是否有与模式串匹配的子串，操作过程也是用模式串去与主串进行比较。而Tire树是多模式串，我们先将模式串提前构建成Tire树，然后查看主串是否匹配模式串，且更适用于类似如上关键词提示的前缀匹配。接下来我们自己通过实现一个简易的关键词提示功能来讲解Tire树。

数据结构

一个value存储当前节点值，用一个26大小的数组存储当前节点的孩子节点，这是一个简单但是可能产生浪费的方法，可以采用有序存入采用二分法查找，或者采用hash表，跳表进行优化。一个标志当前节点是否可作为尾节点。


    public static class node{
        //当前节点值
        private char value;
        //当前节点的孩子节点
        private Node[] childNode;
        //标志当前节点是否是某单词结尾
        private boolean isTail;
        public Node(char value) {
            this.value = value;
        }
    }

初始化

初始化一个仅有root节点的Tire树，root节点值为'/0'。

Node root;
public void init() {
        root = new Node('\0');
        root.childNode = new Node[26];
}

构建字典树

将需要加入的模式串加入Tire树，遍历当前字符串字符，从Tire树根节点开始查找当前字符，如果字符已经存在不需要处理，并且从这个字符节点出发，查看下一个字符是否存在，如果当前节点不存Tire树，才需要插入当前字符，当插入最后一个字符时需要标志当前字符节点为尾节点。


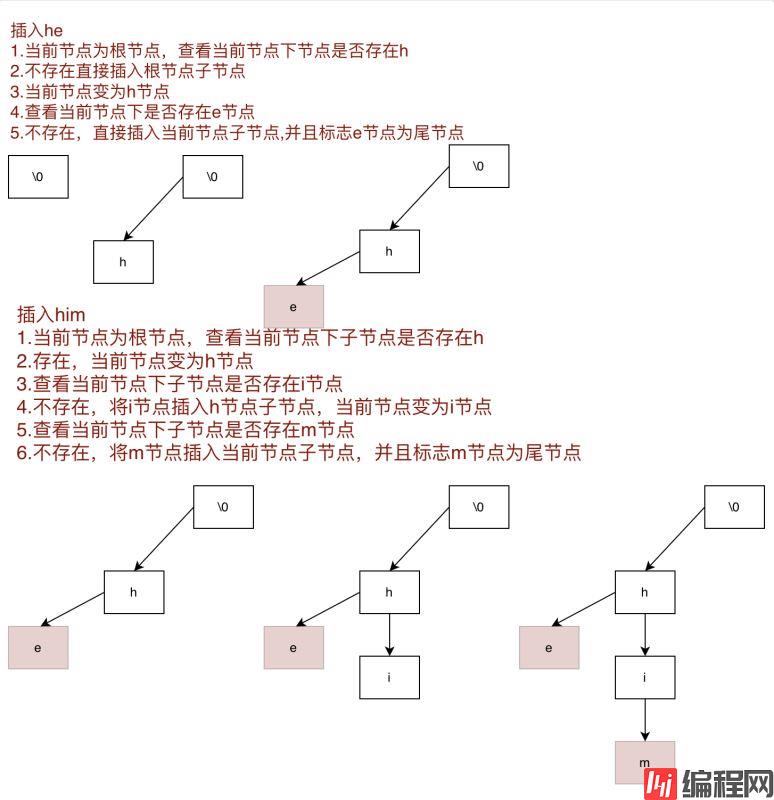
    public void insertStr(char[] chars) {
        //首先判断首字符是否已经在字典树中，然后判断第二字符，依次往下进行判断，找到第一个不存在的字符进行插入孩节点
        Node p = root;
        //表明当前处理到了第几个字符
        int chIndex = 0;
        while (chIndex < chars.length) {
            while (chIndex < chars.length && null != p) {
                Node[] children = p.childNode;
                boolean find = false;
                for (Node child : children) {
                    if (null == child) {continue;}
                    if (child.value == chars[chIndex]) {
                        //当前字符已经存在，不需要再进行存储
                        //从当前节点出发，存储下一个字符
                        p = child;
                        ++ chIndex;
                        find = true;
                        break;
                    }
                }
                if (Boolean.TRUE.equals(find)) {
                    //在孩子中找到了 不用再次存储
                    break;
                }
                //如果把孩子节点都找遍了，还没有找到这个字符，直接将这个字符加入当前节点的孩子节点
                Node node = new Node(chars[chIndex]);
                node.childNode = new Node[26];
                children[chars[chIndex] - 'a'] = node;
                p = node;
                ++ chIndex;
            }
        }
        //字符串中字符全部进入tire树中后，将最后一个字符所在节点标志为结尾节点
        p.isTail = true;
    }

应用

匹配有效单词

遍历字符串，从根节点出发，查看字符是否存在，只要存在不存在的情况，直接返回false，如果每个字符都存在，判断最后一个字符是否为结尾节点，如果不是，到这里还不是一个有效单词，返回false，否则，返回true。

 
    public boolean isMatch(String str) {
        //从root开始进行匹配，只要有一个找不到即为匹配失败
        char[] chars = str.toCharArray();
        int chIndex = 0;
        Node p = root;
        while (null != p) {
            Node[] children = p.childNode;
            boolean flag = false;
            for (Node child : children) {
                if (null == child) {continue;}
                if (child.value == chars[chIndex]) {
                    flag = true;
                    p = child;
                    ++ chIndex;
                    //当比较最后一个字符的时候，这个字符需要是结尾字符才能完全匹配
                    if (chIndex == chars.length && p.isTail) {
                        return true;
                    }
                    break;
                }
            }
            if (Boolean.FALSE.equals(flag)) {
                return false;
            }
        }
        return false;
    }

测试样例

public static void main(String[] args) {
        //he, him, lot, a
        //初始化Tire树
        Trie trie = new Trie();
        trie.init();
        //构建Tire树，只有以下单词才是有效单词
        trie.insertStr("he".toCharArray());
        trie.insertStr("him".toCharArray());
        trie.insertStr("lot".toCharArray());
        trie.insertStr("a".toCharArray());
        //匹配字符串是否为有效单词
        System.out.println(trie.isMatch("lot"));
        System.out.println(trie.isMatch("lit"));

    }

运行结果

关键词提示

根据输入的关键词前缀，匹配所有可能出现的关键词。首先遍历字符串，从节点出发，只要有一个找不到，直接返回null，直至找到最后一个字符对应的节点，从该节点出发找到所有尾节点。

 
    public List<String> findStrPrefix(String str) {
        //根据str首先找到str最后一个字符，然后从这个字符出发，找到所有字符串
        List<String> result = new ArrayList<>();
        char[] chars = str.toCharArray();
        //分成两步走
        //1。找到str最后一个自字符在字典树中的node
        //2。从该node出发，找到所有的结尾node，即为以str为前缀的字符串
        int chIndex = 0;
        Node p = root;
        while (null != p && chIndex < chars.length) {
            Node[] children = p.childNode;
            boolean flag = false;
            for (Node child : children) {
                if (null == child) {continue;}
                if (child.value == chars[chIndex]) {
                    //已经找到
                    p = child;
                    flag = true;
                    ++ chIndex;
                    break;
                }
            }
            //如果没有找到，直接返回空
            if (Boolean.FALSE.equals(flag)) {
                return null;
            }
        }
        //找到了最后一个节点
        //深度优先遍历，查找所有尾节点
        this.dfs(p, new StringBuilder(str), result);
        return result;
    }

    public void dfs(Node p, StringBuilder str, List<String> result) {
        Node[] children = p.childNode;
        for (Node child : children) {
            if (null == child) {
                continue;
            }
            str.append(child.value);
            if (child.isTail) {
                result.add(str.toString());
            }
            //再递归查当前节点的孩子节点
            dfs(child, str, result);
            //需要将刚刚set进去的节点删除，否则影响当前节点的下一个孩子节点
            //举个例子，h的孩子节点有e，i，当e放进去之后不拿出来，在遍历到i的时候，就会形成hei
            str.setLength(str.length() - 1);
        }
    }

测试样例

public static void main(String[] args) {
        //he, him, lot, a
        //初始化Tire树
        Trie trie = new Trie();
        trie.init();
        //构建Tire树，只有以下单词才是有效单词
        trie.insertStr("he".toCharArray());
        trie.insertStr("him".toCharArray());
        trie.insertStr("lot".toCharArray());
        trie.insertStr("a".toCharArray());
        //匹配字符串是否为有效单词
        List<String> strings = trie.findStrPrefix("h");
    }

运行结果