目录一、A*算法介绍二、A*算法步骤解析三、A*算法优化思路3.1、openList使用优先队列(二叉堆)3.2、障碍物列表,closeList 使用二维表(二维数组)3.3、深度限
寻路,即找到一条从某个起点到某个终点的可通过路径。而因为实际情况中,起点和终点之间的直线方向往往有障碍物,便需要一个搜索的算法来解决。
有一定算法基础的同学可能知道从某个起点到某个终点通常使用深度优先搜索(DFS),DFS搜索的搜索方向一般是8个方向(如果不允许搜索斜向,则有4个),但是并无优先之分。
为了让DFS搜索更加高效,结合贪心思想,我们给搜索方向赋予了优先级,直观上离终点最近的方向(直观上的意思是无视障碍物的情况下)为最优先搜索方向,这就是A*算法。
(如下图,绿色为起点,红色为终点,蓝色为不可通过的墙。)

从起点开始往四周各个方向搜索。
(这里的搜索方向有8个方向)

为了区分搜索方向的优先级,我们给每个要搜索的点赋予2个值。
G值(耗费值):指从起点走到该点要耗费的值。
H值(预测值):指从该点走到终点的预测的值(从该点到终点无视障碍物情况下预测要耗费的值,也可理解成该点到终点的直线距离的值)
在这里,值 = 要走的距离
(实际上,更复杂的游戏,因为地形不同(例如陷阱,难走的沙地之类的),还会有相应不同的权值:值 = 要走的距离 * 地形权值)
我们还定义直着走一格的距离等于10,斜着走一格的距离等于14(因为45°斜方向的长度= sqrt(10^2+10^2) ≈ 14)
F值(优先级值):F = G + H
这条公式意思:F是从起点经过该点再到达终点的预测总耗费值。通过计算F值,我们可以优先选择F值最小的方向来进行搜索。
(每个点的左上角为F值,左下角为G值,右下角为H值)

计算出每个方向对应点的F,G,H值后,
还需要给这些点赋予当前节点的指针值(用于回溯路径。因为一直搜下去搜到终点后,如果没有前一个点的指针,我们将无从得知要上次经过的是哪个点,只知道走到终点最终耗费的最小值是多少)
然后我们将这些点放入openList(开启列表:用于存放可以搜索的点)
然后再将当前点放入closeList(关闭列表:用于存放已经搜索过的点,避免重复搜索同一个点)
然后再从openList取出一个F值最小(最优先方向)的点,进行上述同样的搜索。
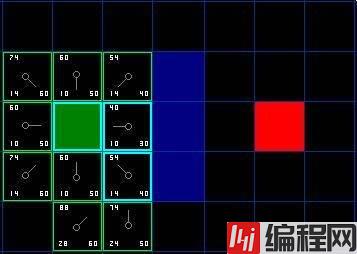
在搜索过程中,如果搜索方向上的点是障碍物或者关闭列表里的点,则跳过之。
通过递归式的搜索,多次搜索后,最终搜到了终点。
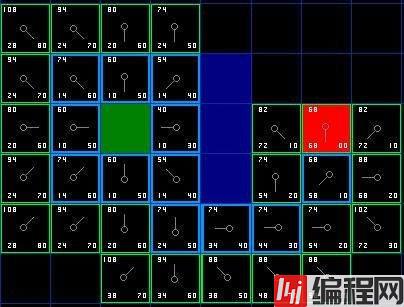
搜到终点后,然后通过前一个点的指针值,我们便能从终点一步步回溯通过的路径点。
(红色标记了便是回溯到的点)
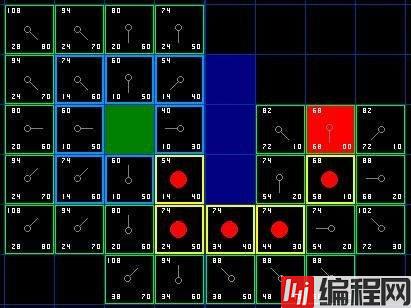
可以看到openlist(开启列表),需要实时添加点,还要每次取出最小值的点。
所以我们可以使用优先队列(二叉堆)来作为openList的容器。
优先队列(二叉堆):插入一个点的复杂度为O(logN),取出一个最值点复杂度为O(logN)
由于障碍物列表和closeList仅用来检测是否能通过,所以我们可以使用bool二维表来存放。
//假设已经定义Width和Height分别为地图的长和宽
bool barrierList[Width][Height];
bool closetList[Width][Height];有某个点(Xa,Yb),可以通过
if(barrierList[Xa][Yb]&&closeList[Xa][Yb])来判断。
因为二维表用下标访问,效率很高,但是耗空间比较多。(三维地图使用三维表则更耗内存。不过现在计算机一般都不缺内存空间,所以尽量提升运算时间为主)
这是一个典型的牺牲内存空间换取运算时间的例子。
有时要搜的路径非常长,利用A*算法搜一次付出的代价很高,造成游戏的卡顿。
那么为了保证每次搜索不会超过一定代价,可以设置深度限制,每搜一次则深度+1,搜到一定深度限制还没搜到终点,则返还失败值。
#include <iOStream>
#include <list>
#include <vector>
#include <queue>
struct OpenPoint{
int x;
int y;
int cost; // 耗费值
int pred; // 预测值
OpenPoint* father; // 父节点
OpenPoint() = default;
OpenPoint(int pX,int pY, int endX, int endY, int c, OpenPoint* fatherp) : x(pX),y(pY),cost(c), father(fatherp) {
//相对位移x,y取绝对值
int relativeX = std::abs(endX - pX);
int relativeY = std::abs(endY - pY);
//x,y偏移值n
int n = relativeX - relativeY;
//预测值pred = (max–n)*14+n*10+c
pred = std::max(relativeX, relativeY) * 14 - std::abs(n) * 4 + c;
}
};
//比较器,用以优先队列的指针类型比较
struct OpenPointPtrCompare {
bool operator()(OpenPoint* a, OpenPoint* b) {
return a->pred > b->pred;
}
};
const int width = 30; //地图长度
const int height = 100; //地图高度
char mapBuffer[width][height]; //地图数据
int depth = 0; //记录深度
const int depthLimit = 2000; //深度限制
bool closeAndBarrierList[width][height]; //记录障碍物+关闭点的二维表
//八方的位置
int direction[8][2] = { {1,0},{0,1},{-1,0},{0,-1},{1,1},{ -1,1 },{ -1,-1 },{ 1,-1 } };
//使用最大优先队列
std::priority_queue<OpenPoint*, std::vector<OpenPoint*>, OpenPointPtrCompare> openlist;
//存储OpenPoint的内存空间
std::vector<OpenPoint> pointList = std::vector<OpenPoint>(depthLimit);
//是否在障碍物或者关闭列表
inline bool inBarrierAndCloseList(int pX,int pY) {
if (pX < 0 || pY < 0 || pX >= width || pY >= height)
return true;
return closeAndBarrierList[pX][pY];
}
//创建一个开启点
inline OpenPoint* createOpenPoint(int pX,int pY,int endX,int endY, int c, OpenPoint* fatherp) {
pointList.emplace_back(pX,pY,endX,endY, c, fatherp);
return &pointList.back();
}
// 开启检查,检查父节点
void open(OpenPoint& pointToOpen, int endX,int endY) {
//将父节点从openlist移除
openlist.pop();
//深度+1
depth++;
//检查p点八方的点
for (int i = 0; i < 4; ++i)
{
int toOpenX = pointToOpen.x + direction[i][0];
int toOpenY = pointToOpen.y + direction[i][1];
if (!inBarrierAndCloseList(toOpenX,toOpenY)) {
openlist.push(createOpenPoint(toOpenX, toOpenY, endX,endY, pointToOpen.cost + 10, &pointToOpen));
}
}
for (int i = 4; i < 8; ++i)
{
int toOpenX = pointToOpen.x + direction[i][0];
int toOpenY = pointToOpen.y + direction[i][1];
if (!inBarrierAndCloseList(toOpenX, toOpenY)) {
openlist.push(createOpenPoint(toOpenX, toOpenY, endX, endY, pointToOpen.cost + 14, &pointToOpen));
}
}
//最后移入closelist
closeAndBarrierList[pointToOpen.x][pointToOpen.y] = true;
}
//开始搜索路径
std::list<OpenPoint*> findway(int startX,int startY, int endX,int endY) {
std::list<OpenPoint*> road;
// 创建并开启一个父节点
openlist.push(createOpenPoint(startX,startY, endX,endY, 0, nullptr));
OpenPoint* toOpen = nullptr;
//重复寻找预测和花费之和最小节点开启检查
while (!openlist.empty())
{
toOpen = openlist.top();
// 找到终点后,则停止搜索
if (toOpen->x == endX && toOpen->y ==endY) {break;}//若超出一定深度(1000深度),则搜索失败
if (depth >= depthLimit) {
toOpen = nullptr;
break;
}
open(*toOpen, endX,endY);
}
for (auto rs = toOpen; rs != nullptr; rs = rs->father) {road.push_back(rs);}
return road;
}
//创建地图
void createMap() {
for (int i = 0; i < width; ++i)
for (int j = 0; j < height; ++j) {
//五分之一概率生成障碍物,不可走
if (rand() % 5 == 0) {
mapBuffer[i][j] = '*';
closeAndBarrierList[i][j] = true;
}
else {
mapBuffer[i][j] = ' ';
closeAndBarrierList[i][j] = false;
}
}
}
//打印地图
void printMap() {
for (int i = 0; i < width; ++i) {
for (int j = 0; j < height; ++j)
std::cout << mapBuffer[i][j];
std::cout << std::endl;
}
std::cout << std::endl << std::endl << std::endl;
}
int main() {
//起点
int beginX = 0;
int beginY = 0;
//终点
int endX = 29;
int endY = 99;
//创建地图
createMap();
//保证起点和终点都不是障碍物
mapBuffer[beginX][beginY] = mapBuffer[endX][endY] = ' ';
closeAndBarrierList[beginX][beginY] = closeAndBarrierList[endX][endY] = false;
//A*搜索得到一条路径
std::list<OpenPoint*> road = findway(beginX,beginY,endX,endY);
//将A*搜索的路径经过的点标记为'O'
for (auto& p : road){mapBuffer[p->x][p->y] = 'O';}
//打印走过路后的地图
printMap();
system("pause");
return 0;
}示例效果:

以上就是如何用C++实现A*寻路算法的详细内容,更多关于C++ A*寻路算法的资料请关注编程网其它相关文章!
--结束END--
本文标题: 如何用C++实现A*寻路算法
本文链接: https://lsjlt.com/news/128275.html(转载时请注明来源链接)
有问题或投稿请发送至: 邮箱/279061341@qq.com QQ/279061341
2024-03-01
2024-03-01
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
回答
回答
回答
回答
回答
回答
回答
回答
回答
回答
0