本篇内容介绍了“什么是二叉堆”的有关知识,在实际案例的操作过程中,不少人都会遇到这样的困境,接下来就让小编带领大家学习一下如何处理这些情况吧!希望大家仔细阅读,能够学有所成!在正式开始学习堆之前,一定要大脑
本篇内容介绍了“什么是二叉堆”的有关知识,在实际案例的操作过程中,不少人都会遇到这样的困境,接下来就让小编带领大家学习一下如何处理这些情况吧!希望大家仔细阅读,能够学有所成!
在正式开始学习堆之前,一定要大脑里回顾一下什么是完全二叉树,因为它和堆可是息息相关奥!
如果二叉树中除了叶子结点,每个结点的度都为 2,则此二叉树称为满二叉树。
而如果二叉树中除去最后一层节点为满二叉树,且最后一层的结点依次从左到右分布,则此二叉树被称为完全二叉树。
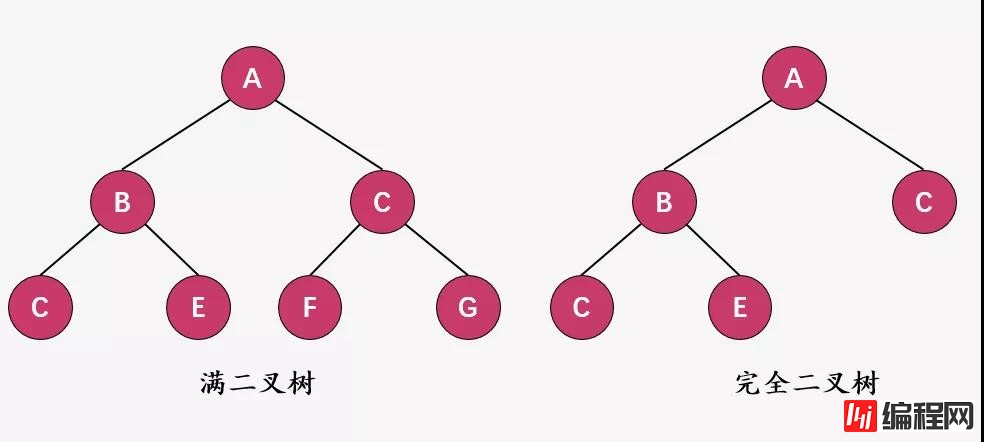
所以可以满二叉树必然是完全二叉树,关于完全二叉树不清楚可以查看 一文读懂有关Tree的前世今生 这篇文章。
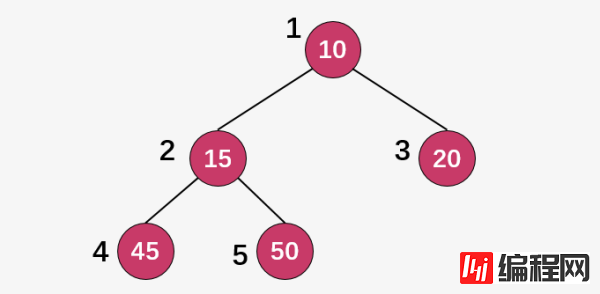
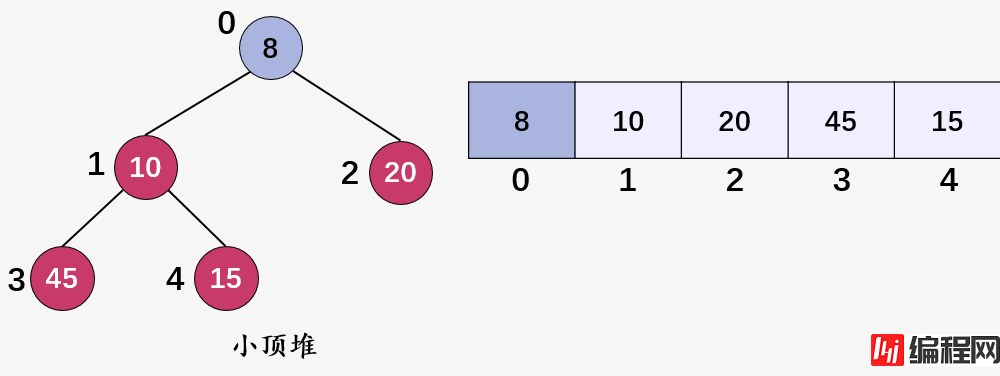
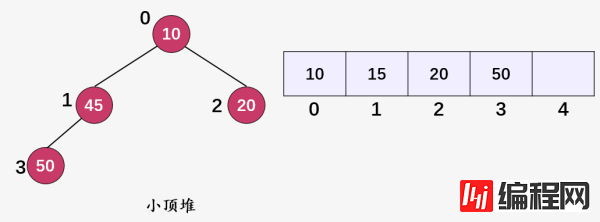
对于任意一个完全二叉树来说,如果将含有的结点按照层次从左到右依次标号(如上图)),对于任意一个结点 i ,完全二叉树(二叉堆)满足以下几个结论:
当i>1时,父亲结点为结点 。i/2时,i=1时,表示的是根结点,无父亲结点);比如结点 45 的的标号为 4 ,其父结点 15 的标号为 2 ,而2=4/2 ;
如果2Xi >n(总结点的个数) ,则结点 肯定没有左孩子(为叶子结点);否则其左孩子是结点2Xi 。比如结点 15 的标号为 2 ,其左孩子结点为 4 ;
如果2X+1 >n,则结点i 肯定没有右孩子;否则右孩子是结点2Xi+1 。
堆堆(Heap)是一类基于完全二叉树的特殊数据结构。通常将堆分为两种类型:
大顶堆(Max Heap):在大顶堆中,根结点的值必须大于它的孩子结点的值,对于二叉树中所有子树也应递归地满足这一特性。
小顶堆(Min Heap):在小顶堆中,根结点的值必须小于它的孩子结点的值,且对于二叉树的所有子树也均递归地满足同一特性。
不是所有的人都是计算机出身,上过正课的小伙伴,所以我在唠叨一下概念。
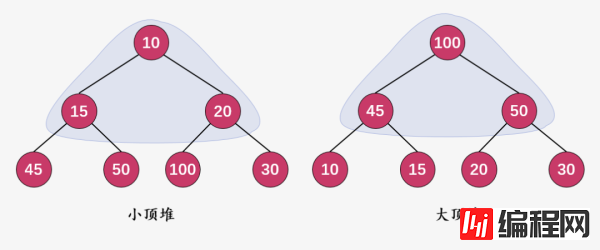
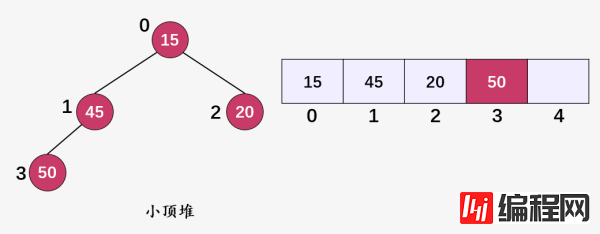
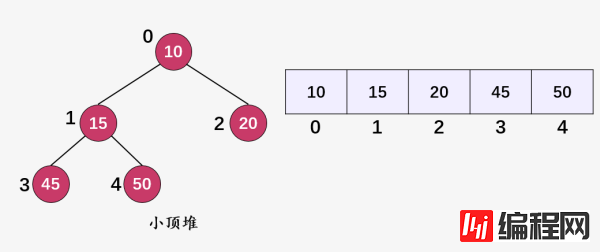
小顶堆就是以任意一个结点作为根,其左右孩子都要大于等于该结点的值,所以整颗树的根结点一定是树中值最小的结点,而大顶堆正好特性相反。
二叉堆
二叉堆是满足下面属性的一颗二叉树:
二叉堆必定是一颗完全二叉树。二叉堆的此属性也决定了他们适合存储在数组当中。
二叉堆要么是小顶堆,要么是大顶堆。小顶二叉堆中的根结点的值是整棵树中的最小值,而且二叉树中的所有顶点及其子树均满足这一特性。大顶堆与小顶堆类似,大顶堆的根结点的值是整棵树中的最大值,而且二叉树中所有结点的值也均大于等于其子树结点。
由于小顶堆和大顶堆除了在顶点的大小关系上不一致,两者均是一颗全完二叉树,下面的所有讲解,都以小顶堆为例进行说明,会了小顶堆,大顶堆你自己都能写出来。
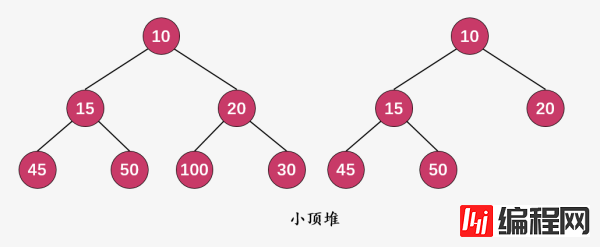
这就是两个典型的小顶堆。
二叉堆的存储结构
二叉堆是一颗完全二叉树,一般用数组表示。其中根元素用 arr[0] 表示,而其他结点(第i 个结点的存储位置)满足下表中的特性:
数组表示含义
| 数组表示 | 含义 |
|---|---|
| arr[(i-1)/2] | 第 i 个结点的父结点 |
| arr[2*i + 1] | 第 i 个结点的左孩子结点 |
| arr[2*i + 2] | 第 i 个结点的右孩子结点 |
二叉堆的这种表示方式和性质其本质上与一颗完全二叉树自身所具有的特性一一对应。
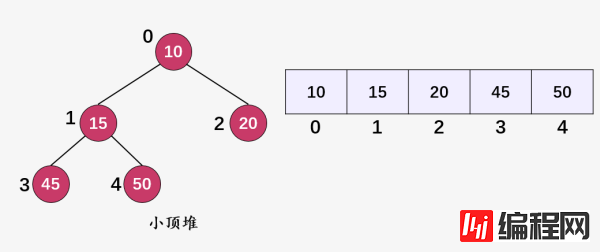
小顶二叉堆的常见操作
获取小顶二叉堆的根元素 getMin() ,这一操作的时间复杂度为 ;按照上面的存储结构,根结点为 arr[0] ,返回即可。
int getMin() { return arr[0]; }移除小顶二叉堆的最小元素 removeMin() ,这一操作的时间复杂度为 ,因为移除小顶二叉堆的最小元素(即堆顶元素)之后,需要对堆进行调整,从而使得堆依旧维持其属性,一般将调整的过程称为 堆化 (heapify)。
int removeMin() { if (heap_size <= 0) return INT_MAX; if (heap_size == 1) { heap_size--; return harr[0]; } // 存储最小值(当前的堆顶元素),将堆中的最后一个元素放到堆顶,然后进行Heapify() int root = harr[0]; harr[0] = harr[heap_size-1]; heap_size--; MinHeapify(0); return root; }我们以下图为例进行说明:
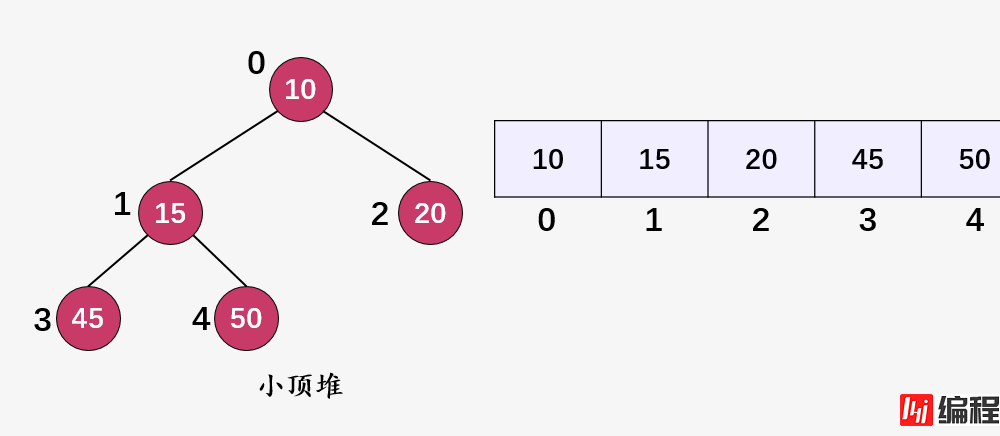
删除堆顶元素 10 ,然后将最后一个元素 50 作为小顶堆的堆顶:
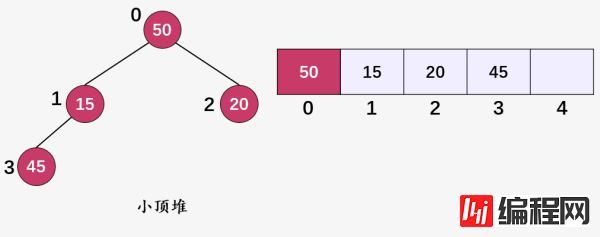
然后从堆顶元素 50 开始进行堆化。
第一步:计算当前堆顶元素 50(i = 0) 的左孩子 ,以及右孩子 ,然后比较三者,选择出三者的最小值 15 ,将 15 和 50 进行交换,继续对值为 50 的顶点(i = 1)的子树进行堆化:
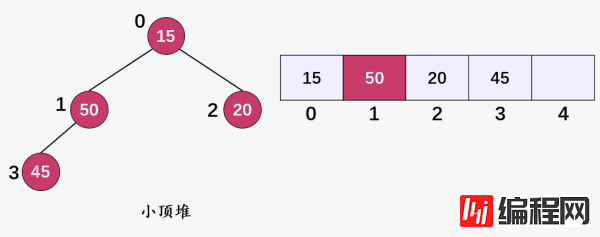
第二步:计算当前要进行堆化的结点 50(i = 1) 的左右孩子,左孩子 ,右孩子不存在,比较 50 和 45 ,发现 50 > 45 ,交换两者,然后继续对值为 50 的顶点(i = 3)的子树进行堆化:
第三步:计算要进行堆化的结点 50 (i = 1) 的左右孩子,发现不存在,所以结点 50 已经到叶子结点,整棵树堆化完成啦(其实这个堆化的过程还是挺简单的,我们后面删除等还会用到堆化的,这里不明白,不影响下面继续哒!)。
更新给定下标的值 updateKey(int i,int new_val) ,这里有一个假设是 new_val < val 的值,如果 new_val > val ,那么就是对更新的结点进行堆化啦,所以就不单独进行处理。还想两种都处理,加个 If...else... 就可以啦。
void updateKey(int i, int new_val) { harr[i] = new_val; while (i != 0 && harr[parent(i)] > harr[i]) { swap(&harr[i], &harr[parent(i)]); i = parent(i); } }这个操作和堆化的操作相反,我们是从被更新的结点开始向上回溯,直到结点的值大于父结点的值停止。
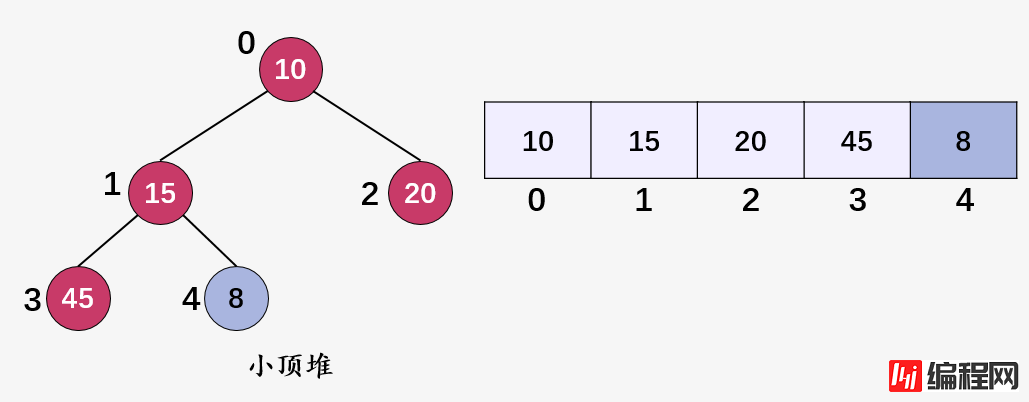
我们将下标为 4 的结点 50 的值更新为 8 :
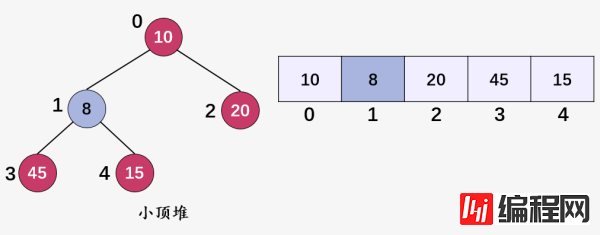
第一步:判断结点 8(i = 4) 的父结点 的大小关系,8 < 15 ,交换 8和 15 ,然后结点 8(i = 1) 继续做判断:
的大小关系,8 < 15 ,交换 8和 15 ,然后结点 8(i = 1) 继续做判断:
第二步:判断结点 8(i = 1) 与其父节点 的大小关系,8 < 10 , 交换8 和10 :
的大小关系,8 < 10 , 交换8 和10 :
第三步:判断结点 8(i = 0),发现其本身已为根结点,没有父结点,更新结束。
更新结点值的时间复杂度也为 ,即为树高。
插入结点 insert() :插入一个新结点的时间复杂度也为 。将一个新结点插入到树的末尾,如果新结点的值大于其父结点的值,插入就直接完成了;否则,类似于 updateKey() 操作,向上回溯修正堆。
void insert(int k) { if (heap_size == capacity) { cout << "\n溢出:无法插入\n"; return; } // 将新插入的结点插入最后一个位置 heap_size - 1 heap_size++; int i = heap_size - 1; harr[i] = k; // 如果违反堆的性质,则向上回溯进行修正 while (i != 0 && harr[parent(i)] > harr[i]) { swap(&harr[i], &harr[parent(i)]); i = parent(i); } }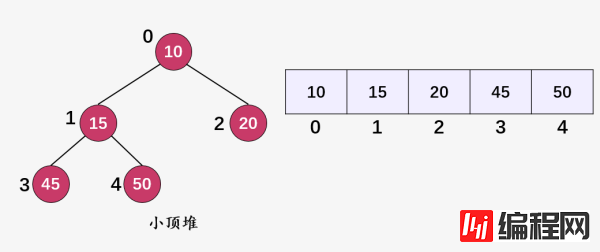
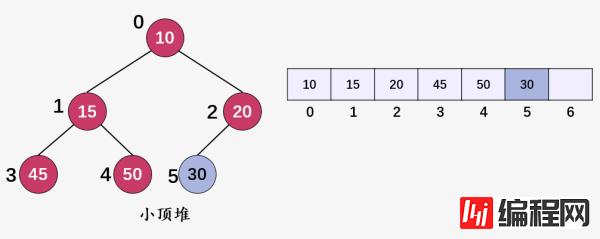
比如,我们插入结点 30(i = 5) ,由于其值大于父结点的值 20 ,并没有违反堆的属性,直接插入完成。
在插入结点 30 的基础上,我们再插入结点 9(i = 6) :
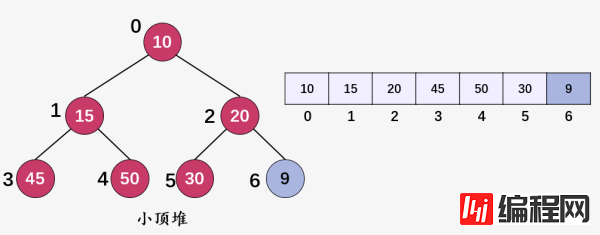
新插入结点的值 9(i = 6) 小于父结点 20(i = 2) 的值,故交换结点 9 和 20 ,然后继续判断值为 9(i = 2) :
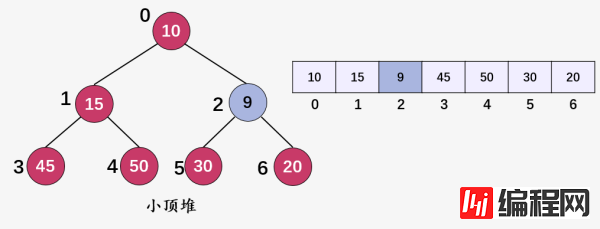
判断结点 9(i = 2) 与其结点 10(i = 0) 的值, 9 < 10 ,交换 9 和 10 ,然后继续判断值9(i = 2) :
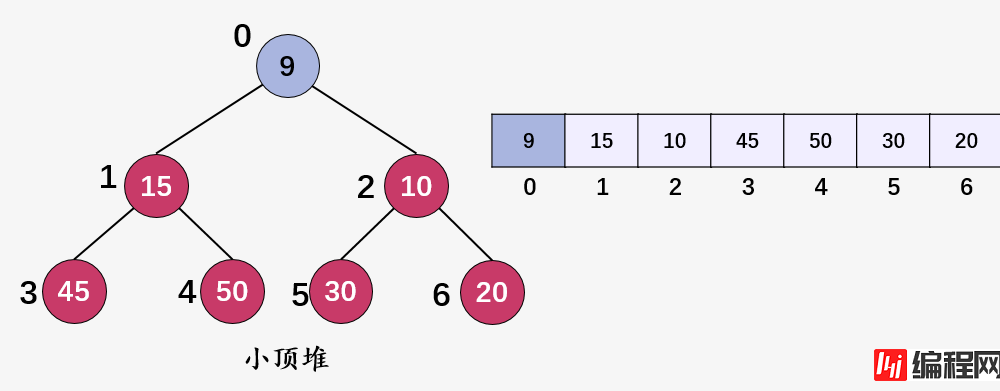
发现值 9(i = 2) 已经是根结点了,插入完成。
删除结点 delete() : 删除一个结点的时间复杂度也是 。将要删除的结点用无穷小 INT_MIN 替换,即调用 updateKey(i, INT_MIN) ; 然后再将堆顶元素 INT_MIN 移除,即调用 removeMin() 。
void delete(int i) { updateKey(i, INT_MIN); removeMin(); }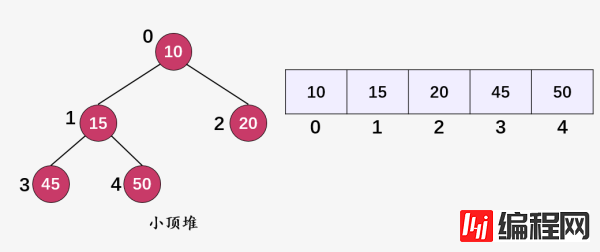
比如,我们删除结点 15(i = 1) ,第一步,调用 update(1, INT_MIN) 将该结点的值替换为INT_MIN :
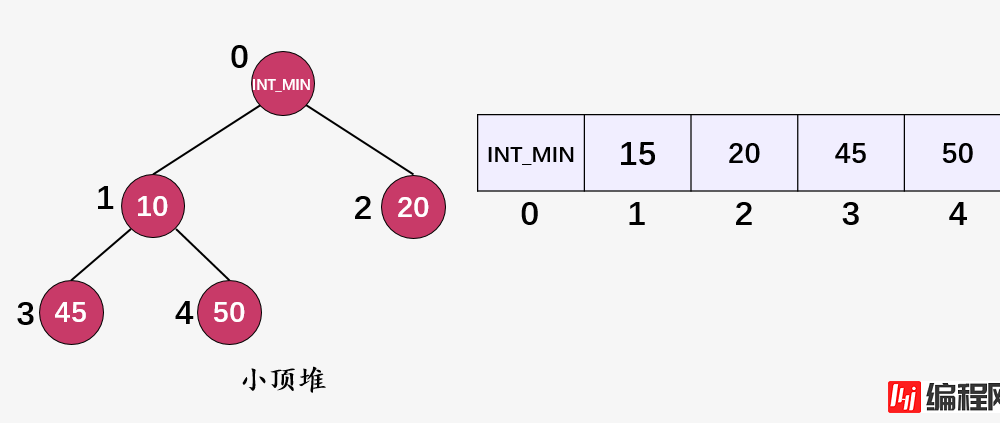
第二步:调用 removeMin() 函数将 INT_MIN 移除即可。
最后再来看一下 removeMin() 函数中提到的堆化操作的实现代码(结合前面介绍removeMin() 函数时堆化的图文):
void Heapify(int i) { int l = left(i); //结点 i 的左孩子下标 2i + 1 int r = right(i); //结点 i 的右孩子小标 2i + 2 int samllest = i; if(l < heap_size && arr[l] < arr[i]) { smallest = l; } if(r < heap_size && arr[r] < arr[smallest]) { smallest = r; } if(smallist != i) { swap(&arr[i], &arr[smallest]); Heapify(smallest); } }关于二叉堆的基本操作就介绍完了,因为二叉堆不论在考试还是面试中是最常见的,所以建议一定要搞懂奥!
堆的应用
一、堆排序(Heap Sort):堆排序可以使用二叉堆在 的时间内对数组完成排序,这也是今天先讲二叉堆的原因。
二、优先队列(Priority Queue):使用二叉堆,可以实现一个高效的优先队列,因为二叉堆的各类操作的时间复杂度均为 。(优先队列好像我没讲,以后有机会一定更新)
三、图算法(Graph AlGorithms):优先队列广泛应用于像迪杰斯特拉算法和普里姆算法的图算法当中
“什么是二叉堆”的内容就介绍到这里了,感谢大家的阅读。如果想了解更多行业相关的知识可以关注编程网网站,小编将为大家输出更多高质量的实用文章!
--结束END--
本文标题: 什么是二叉堆
本文链接: https://lsjlt.com/news/84691.html(转载时请注明来源链接)
有问题或投稿请发送至: 邮箱/279061341@qq.com QQ/279061341
2024-01-12
2023-05-20
2023-05-20
2023-05-20
2023-05-20
2023-05-20
2023-05-20
2023-05-20
2023-05-20
2023-05-20
回答
回答
回答
回答
回答
回答
回答
回答
回答
回答
0