小数的表示方法之怎么使用定点数

本篇内容主要讲解“小数的表示方法之怎么使用定点数”，感兴趣的朋友不妨来看看。本文介绍的方法操作简单快捷，实用性强。下面就让小编来带大家学习“小数的表示方法之怎么使用定点数”吧!

在数字信号处理中往往都需要进行大量的数字运算，比如，数字信号的解调，需要采集大量的IQ数据对其进行解调运算。在实际的研究和学习中我们一般会在操作系统中利用丰富的软件给我们提供的便捷的计算工具进行计算(Matlab、python等)，这可以很方便的处理我们所研究的数字信号。然而，学过计算机原理或者汇编语言的同学会清楚，数据的运算的最终是在计算机硬件上来完成的，我们在操作系统层面的数据运算往往意味着需要进行大量的资源的调度。

虽然现在的计算机的性能已经非常的强大，但是对于面向应用的产品来说，其处理器性能往往和计算机不能相提并论。

通常，在通信、图像等数字信号处理中，会采用硬件芯片的方式进行数据运算(DSP、FPGA等)，通过这种硬件芯片上进行数字信号运算，可以很好的提高运算效率，这也在工程应用中广为采用的一种方式。

在这些处理器中往往各种数据都是通过整数形式存储(比如，通信中的IQ数值的存储)。实际上，我们需要进行运算的数据大多都是小数，那么，该怎么解决呢?一般的我们可以通过定点数这种方式来表示小数。

什么是定点数

定点数英文名叫Fixed Point  Number，其关键地方就在定和点这两个字上面，即在表示小数数据时，把小数点的位置已经约定好固定在某个位置。与之对应的是浮点数，其小数点的位置不是固定的，关于浮点数先不做展开。

定数表示

在定点数中，小数点可以将数据分为整数和小数部分，因此我们可以约定小数点在数据中的不同位置，就可以表示不同大小和精度的小数。例如，当小数点位置约定在符号位和数值位之间，就表示纯小数;当小数点约定在最末尾位置时，就可以表示纯整数。

纯小数

纯整数

如何描述定点数的这种规则呢?其实，我们可以使用两种方法来表示：

• Q来表示法Qx，x表示小数的位数。

• S表示法Sx.y，x表示整数位数，y表示小数位数。

我们知道在计算机中根据是否存在符号位可以分成无符号整数和有符号整数，当然，对于定点数也可以根据有无符号位分为：

• 无符号定点数：无符号位

• 有符号定点数：有符号位

无符号定点数

无符号定点数，数值在机器中字长的全部二进制位中没有符号位，全都是数值位。例如，小数1.2转换成16位的定数，小数点的位置约定在第14位和第15位之间。

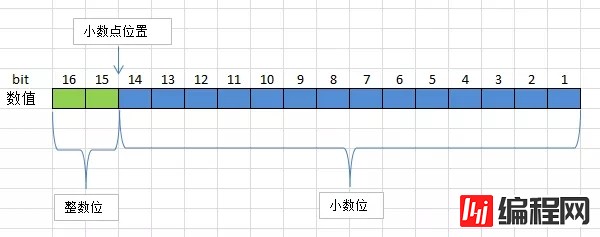
无符号Q14

根据计算结果，小数1.2可以用Q14格式的无符号定点数19661表示。

无符号定点数比较简单，不存在负小数;但是，有符号定点数就没这么简单了，因为存在正负数，其计算方法也不尽相同。

原码、反码、补码

原码、反码、补码在大多数的计算机编程相关的书籍里基本上都会提到。在学习有符号定点数之前，我们需要先复习一下原码、反码和补码。因为数据在计算中的存储方式是以补码的形式存储的，在学习有符号定点数之前，所以，我们有必要先复习这部分内容。

• 原码：最高位作为符号位(无符号则没有符号位)，其他位是数据二进制真值绝对值。例如，无符号数5，其8位二进制数的原码为0000  0101;有符号数5，其8位二进制的原码为0000 0101;有符号数-5，其8位二进制的原码1000 0101。

• 反码：正数的反码是其原码本身，负数的反码在其原码的基础上符号位不变，其他位取反。例如，无符号数5，其8位二进制数的反码为0000  0101;有符号数5，其8位二进制数的反码为0000 0101;而有符号数-5，其8位二进制的反码为1111 1010。

• 补码：正数的补码就是其本身，负数的补码是在其反码基础上加1。例如，无符号数5，其8位二进制数的补码为0000  0101;有符号数5，其8位二进制数的补码为0000 0101;而有符号数-5，其8位二进制的补码为1111 1011。

对于正数来说，

原码 = 反码 = 补码

对于负数来说，

反码 = 符号位不变，原码取反 补码 = 反码 + 1

有符号定点数

有符号定点数，需要专门取一位数据位作为符号位，通常，符号位上的1表示负数，0表示正数，其余位为数值位。例如，将小数0.8和-0.8转成Q15格式的定点数。

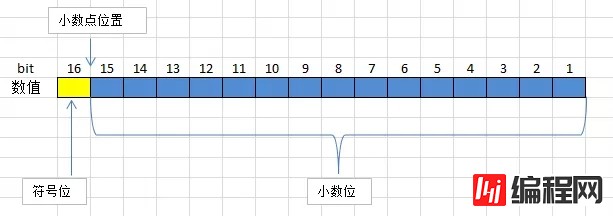
有符号Q15

求正数0.8的定点数：

求负数-0.8的定点数：

在有符号定点数中，需要要注意负数的计算与正数有所不同。

到此，相信大家对“小数的表示方法之怎么使用定点数”有了更深的了解，不妨来实际操作一番吧！这里是编程网网站，更多相关内容可以进入相关频道进行查询，关注我们，继续学习！