【运筹优化】拉格朗日松弛 & 次梯度算法求解整数规划问题 + Java调用Cplex实战

文章目录

• 一、拉格朗日松弛
• 二、次梯度算法
• 三、案例实战

一、拉格朗日松弛

当遇到一些很难求解的模型，但又不需要去求解它的精确解，只需要给出一个次优解或者解的上下界，这时便可以考虑采用松弛模型的方法加以求解。

对于一个整数规划问题，拉格朗日松弛放松模型中的部分约束。这些被松弛的约束并不是被完全去掉，而是利用拉格朗日乘子在目标函数上增加相应的惩罚项，对不满足这些约束条件的解进行惩罚。

拉格朗日松弛之所以受关注，是因为在大规模的组合优化问题中，若能在原问题中减少一些造成问题“难”的约束，则可使问题求解难度大大降低，有时甚至可以得到比线性松弛更好的上下界。

二、次梯度算法

由于拉格朗日对偶问题通常是分段线性的，这会导致其在某些段上不可导，所以没法使用常规的梯度下降法处理。于是引入次梯度（Subgradient）用于解决此类目标函数并不总是处处可导的问题。

次梯度算法的优势是比传统方法能够处理的问题范围更大，不足之处就是算法收敛速度慢。

三、案例实战

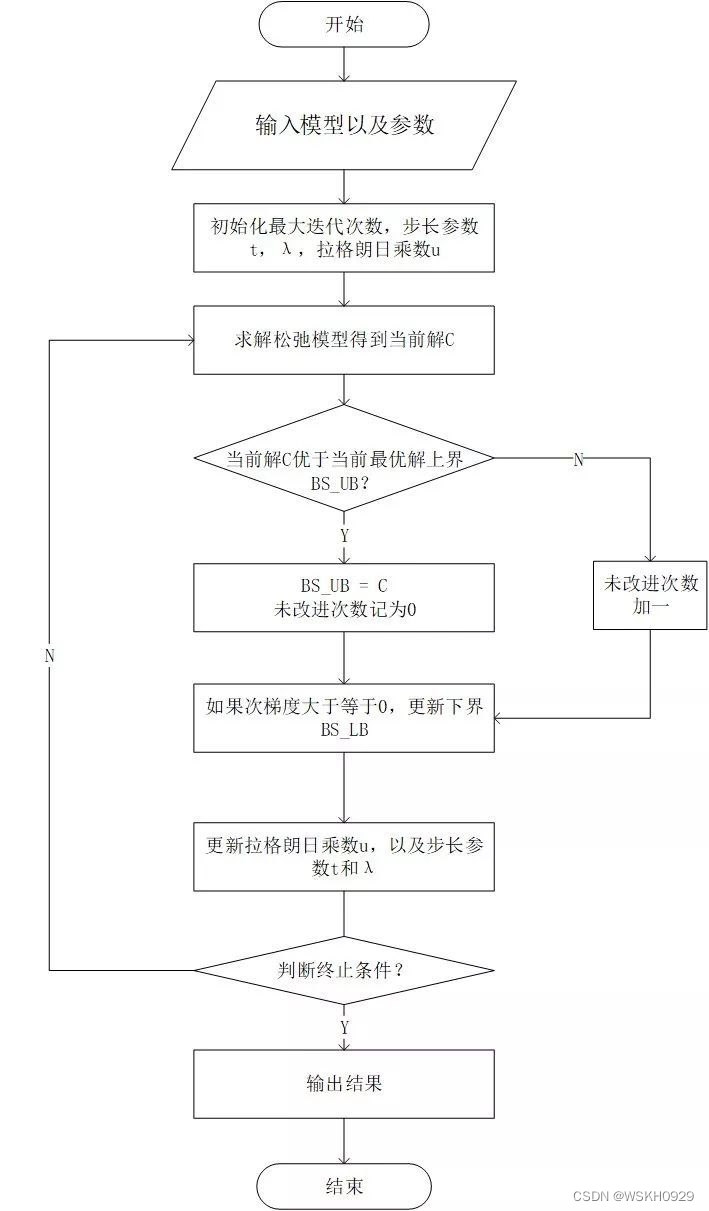
松弛之后的目标函数为

$$max:z=16x_1+10x_2+4x_4+\mu [10-(8x_1+2x_2+x_3+4x_4)]$$

化简为

$$max:z=(16-8\mu )x_1+(10-2\mu )x_2+(-\mu )x_3+(4-4\mu )x_4+10\mu$$

由于每一次迭代时 $\mu$ 是一个确定的常数，所以目标函数中的 $10\mu$ 可以在建模时省略

具体求解代码如下：

import ilog.concert.IloException;import ilog.concert.IloIntVar;import ilog.concert.IloLinearNumExpr;import ilog.cplex.IloCplex;import java.util.Arrays;public class TestLR {    // lambda    static double lambda = 2d;    // 最大迭代次数    static int epochs = 100;    // 上界最大未更新次数    static int ubMaxNonImproveCnt = 3;    // 最小步长    static double minStep = 0.001;    // 松弛问题模型    static IloCplex relaxProblemModel;    // 变量数组    static IloIntVar[] intVars;    // 最佳上下界    static double bestLB = 0d;    static double bestUB = 1e10;    // 最佳拉格朗日乘数    static double bestMu = 0d;    // 最佳解    static double[] bestX;    // 运行主函数    public static void run() throws IloException {        //        double mu = 0d;        double step = 1d;        int ubNonImproveCnt = 0;        // 初始化松弛问题模型        initRelaxModel();        // 开始迭代        for (int epoch = 0; epoch < epochs; epoch++) {            System.out.println("----------------------------- Epoch-" + (epoch + 1) + " -----------------------------");            System.out.println("mu: " + mu);            System.out.println("lambda: " + lambda);            // 根据mu，设置松弛问题模型目标函数            setRelaxModelObjectiveBuMu(mu);            if (relaxProblemModel.solve()) {                // 获得当前上界（由于建模时没有考虑常数 10*mu，所以这里要加回来，得到松弛问题的真正目标值）                double curUB = relaxProblemModel.getObjValue() + 10 * mu;                // 更新上界                if (curUB < bestUB) {                    bestUB = curUB;                    ubNonImproveCnt = 0;                } else {                    ubNonImproveCnt++;                }                System.out.println("curUB: " + curUB);                // 获取变量值                double[] x = relaxProblemModel.getValues(intVars);                // 计算次梯度                double subGradient = (8 * x[0] + 2 * x[1] + x[2] + 4 * x[3]) - 10;                double dist = Math.pow(subGradient, 2);                // 迭迭代停止条件1                if (dist <= 0.0) {                    System.out.println("Early stop: dist (" + dist + ") <= 0 !");                    break;                }                // 如果次梯度大于等于0，说明满足被松弛的约束，即可以作为原问题的可行解                if (subGradient <= 0) {                    // 计算当前原问题的解值                    double obj = 16 * x[0] + 10 * x[1] + 4 * x[3];                    if (obj > bestLB) {                        // 更新下界                        bestLB = obj;                        bestMu = mu;                        bestX = x.clone();                    }                }                System.out.println("subGradient: " + subGradient);                System.out.println("bestUB: " + bestUB);                System.out.println("bestLB: " + bestLB);                System.out.println("gap: " + String.fORMat("%.2f", (bestUB - bestLB) * 100d / bestUB) + " %");                // 迭代停止条件2                if (bestLB >= bestUB - 1e-06) {                    System.out.println("Early stop: bestLB (" + bestLB + ") >= bestUB (" + bestUB + ") !");                    break;                }                // 上界未更新达到一定次数                if (ubNonImproveCnt >= ubMaxNonImproveCnt) {                    lambda /= 2;                    ubNonImproveCnt = 0;                }                // 更新拉格朗日乘数                mu = Math.max(0, mu + step * subGradient);                // 更新步长                step = lambda * (curUB - bestLB) / dist;                // 迭代停止条件3                if (step < minStep) {                    System.out.println("Early stop: step (" + step + ") is less than minStep (" + minStep + ") !");                    break;                }            } else {                System.err.println("Lagrange relaxation problem has no solution!");            }        }    }    // 建立松弛问题模型    private static void initRelaxModel() throws IloException {        relaxProblemModel = new IloCplex();        relaxProblemModel.setOut(null);        // 声明4个整数变量        intVars = relaxProblemModel.intVarArray(4, 0, 1);        // 添加约束        // 约束1：x1+x2<=1        relaxProblemModel.addLe(relaxProblemModel.sum(intVars[0], intVars[1]), 1);        // 约束2：x3+x4<=1        relaxProblemModel.addLe(relaxProblemModel.sum(intVars[2], intVars[3]), 1);    }    // 根据mu，设置松弛问题模型的目标函数    private static void setRelaxModelObjectiveBuMu(double mu) throws IloException {        // 目标函数（省略了常数 10*mu）        IloLinearNumExpr target = relaxProblemModel.linearNumExpr();        target.addTerm(16 - 8 * mu, intVars[0]);        target.addTerm(10 - 2 * mu, intVars[1]);        target.addTerm(0 - mu, intVars[2]);        target.addTerm(4 - 4 * mu, intVars[3]);        if (relaxProblemModel.getObjective() == null) {            relaxProblemModel.addMaximize(target);        } else {            relaxProblemModel.getObjective().setExpr(target);        }    }    public static void main(String[] args) throws IloException {        long s = System.currentTimeMillis();        run();        System.out.println("----------------------------- Solution -----------------------------");        System.out.println("bestMu: " + bestMu);        System.out.println("bestUB: " + bestUB);        System.out.println("bestLB: " + bestLB);        System.out.println("gap: " + String.format("%.2f", (bestUB - bestLB) * 100d / bestUB) + " %");        System.out.println("bestX: " + Arrays.toString(bestX));        System.out.println("Solve Time: " + (System.currentTimeMillis() - s) + " ms");    }}

程序输出：

----------------------------- Epoch-1 -----------------------------mu: 0.0lambda: 2.0curUB: 20.0subGradient: 2.0bestUB: 20.0bestLB: 0.0gap: 100.00 %----------------------------- Epoch-2 -----------------------------mu: 2.0lambda: 2.0curUB: 26.0subGradient: -8.0bestUB: 20.0bestLB: 10.0gap: 50.00 %----------------------------- Epoch-3 -----------------------------mu: 0.0lambda: 2.0curUB: 20.0subGradient: 2.0bestUB: 20.0bestLB: 10.0gap: 50.00 %----------------------------- Epoch-4 -----------------------------mu: 1.0lambda: 2.0curUB: 18.0subGradient: 2.0bestUB: 18.0bestLB: 10.0gap: 44.44 %----------------------------- Epoch-5 -----------------------------mu: 11.0lambda: 2.0curUB: 110.0subGradient: -10.0bestUB: 18.0bestLB: 10.0gap: 44.44 %----------------------------- Epoch-6 -----------------------------mu: 0.0lambda: 2.0curUB: 20.0subGradient: 2.0bestUB: 18.0bestLB: 10.0gap: 44.44 %----------------------------- Epoch-7 -----------------------------mu: 4.0lambda: 2.0curUB: 42.0subGradient: -8.0bestUB: 18.0bestLB: 10.0gap: 44.44 %----------------------------- Epoch-8 -----------------------------mu: 0.0lambda: 1.0curUB: 20.0subGradient: 2.0bestUB: 18.0bestLB: 10.0gap: 44.44 %----------------------------- Epoch-9 -----------------------------mu: 1.0lambda: 1.0curUB: 18.0subGradient: 2.0bestUB: 18.0bestLB: 10.0gap: 44.44 %----------------------------- Epoch-10 -----------------------------mu: 6.0lambda: 1.0curUB: 60.0subGradient: -10.0bestUB: 18.0bestLB: 10.0gap: 44.44 %----------------------------- Epoch-11 -----------------------------mu: 0.0lambda: 0.5curUB: 20.0subGradient: 2.0bestUB: 18.0bestLB: 10.0gap: 44.44 %----------------------------- Epoch-12 -----------------------------mu: 0.5lambda: 0.5curUB: 19.0subGradient: 2.0bestUB: 18.0bestLB: 10.0gap: 44.44 %----------------------------- Epoch-13 -----------------------------mu: 3.0lambda: 0.5curUB: 34.0subGradient: -8.0bestUB: 18.0bestLB: 10.0gap: 44.44 %----------------------------- Epoch-14 -----------------------------mu: 0.0lambda: 0.25curUB: 20.0subGradient: 2.0bestUB: 18.0bestLB: 10.0gap: 44.44 %----------------------------- Epoch-15 -----------------------------mu: 0.1875lambda: 0.25curUB: 19.625subGradient: 2.0bestUB: 18.0bestLB: 10.0gap: 44.44 %----------------------------- Epoch-16 -----------------------------mu: 1.4375lambda: 0.25curUB: 21.5subGradient: -8.0bestUB: 18.0bestLB: 10.0gap: 44.44 %----------------------------- Epoch-17 -----------------------------mu: 0.0lambda: 0.125curUB: 20.0subGradient: 2.0bestUB: 18.0bestLB: 10.0gap: 44.44 %----------------------------- Epoch-18 -----------------------------mu: 0.044921875lambda: 0.125curUB: 19.91015625subGradient: 2.0bestUB: 18.0bestLB: 10.0gap: 44.44 %----------------------------- Epoch-19 -----------------------------mu: 0.669921875lambda: 0.125curUB: 18.66015625subGradient: 2.0bestUB: 18.0bestLB: 10.0gap: 44.44 %----------------------------- Epoch-20 -----------------------------mu: 1.289306640625lambda: 0.0625curUB: 20.314453125subGradient: -8.0bestUB: 18.0bestLB: 10.0gap: 44.44 %----------------------------- Epoch-21 -----------------------------mu: 0.206787109375lambda: 0.0625curUB: 19.58642578125subGradient: 2.0bestUB: 18.0bestLB: 10.0gap: 44.44 %----------------------------- Epoch-22 -----------------------------mu: 0.22693252563476562lambda: 0.0625curUB: 19.54613494873047subGradient: 2.0bestUB: 18.0bestLB: 10.0gap: 44.44 %----------------------------- Epoch-23 -----------------------------mu: 0.5265083312988281lambda: 0.03125curUB: 18.946983337402344subGradient: 2.0bestUB: 18.0bestLB: 10.0gap: 44.44 %----------------------------- Epoch-24 -----------------------------mu: 0.6756666898727417lambda: 0.03125curUB: 18.648666620254517subGradient: 2.0bestUB: 18.0bestLB: 10.0gap: 44.44 %----------------------------- Epoch-25 -----------------------------mu: 0.8154633045196533lambda: 0.03125curUB: 18.369073390960693subGradient: 2.0bestUB: 18.0bestLB: 10.0gap: 44.44 %----------------------------- Epoch-26 -----------------------------mu: 0.9505987204611301lambda: 0.015625curUB: 18.09880255907774subGradient: 2.0bestUB: 18.0bestLB: 10.0gap: 44.44 %----------------------------- Epoch-27 -----------------------------mu: 1.0159821063280106lambda: 0.015625curUB: 18.127856850624084subGradient: -8.0bestUB: 18.0bestLB: 10.0gap: 44.44 %----------------------------- Epoch-28 -----------------------------mu: 0.7628945263568312lambda: 0.015625curUB: 18.474210947286338subGradient: 2.0bestUB: 18.0bestLB: 10.0gap: 44.44 %----------------------------- Epoch-29 -----------------------------mu: 0.766863206459675lambda: 0.0078125curUB: 18.46627358708065subGradient: 2.0bestUB: 18.0bestLB: 10.0gap: 44.44 %----------------------------- Epoch-30 -----------------------------mu: 0.7999655929725122lambda: 0.0078125curUB: 18.400068814054976subGradient: 2.0bestUB: 18.0bestLB: 10.0gap: 44.44 %----------------------------- Epoch-31 -----------------------------mu: 0.833036974172046lambda: 0.0078125curUB: 18.333926051655908subGradient: 2.0bestUB: 18.0bestLB: 10.0gap: 44.44 %----------------------------- Epoch-32 -----------------------------mu: 0.8658497429769483lambda: 0.00390625curUB: 18.268300514046103subGradient: 2.0bestUB: 18.0bestLB: 10.0gap: 44.44 %----------------------------- Epoch-33 -----------------------------mu: 0.8821269422965887lambda: 0.00390625curUB: 18.235746115406823subGradient: 2.0bestUB: 18.0bestLB: 10.0gap: 44.44 %----------------------------- Epoch-34 -----------------------------mu: 0.8982759667380851lambda: 0.00390625curUB: 18.20344806652383subGradient: 2.0bestUB: 18.0bestLB: 10.0gap: 44.44 %----------------------------- Epoch-35 -----------------------------mu: 0.914361408369739lambda: 0.001953125curUB: 18.17127718326052subGradient: 2.0bestUB: 18.0bestLB: 10.0gap: 44.44 %----------------------------- Epoch-36 -----------------------------mu: 0.9223725881222037lambda: 0.001953125curUB: 18.155254823755595subGradient: 2.0bestUB: 18.0bestLB: 10.0gap: 44.44 %----------------------------- Epoch-37 -----------------------------mu: 0.9303523509964815lambda: 0.001953125curUB: 18.13929529800704subGradient: 2.0bestUB: 18.0bestLB: 10.0gap: 44.44 %----------------------------- Epoch-38 -----------------------------mu: 0.9383164670353054lambda: 9.765625E-4curUB: 18.123367065929386subGradient: 2.0bestUB: 18.0bestLB: 10.0gap: 44.44 %----------------------------- Epoch-39 -----------------------------mu: 0.9422907323175354lambda: 9.765625E-4curUB: 18.11541853536493subGradient: 2.0bestUB: 18.0bestLB: 10.0gap: 44.44 %----------------------------- Epoch-40 -----------------------------mu: 0.9462572201426962lambda: 9.765625E-4curUB: 18.107485559714608subGradient: 2.0bestUB: 18.0bestLB: 10.0gap: 44.44 %Early stop: step (9.896832958635996E-4) is less than minStep (0.001) !----------------------------- Solution -----------------------------bestMu: 2.0bestUB: 18.0bestLB: 10.0gap: 44.44 %bestX: [0.0, 1.0, 0.0, 0.0]Solve Time: 152 ms

分析：
从最终结果可以看到， bestLB 为10，也就是通过拉格朗日松弛&次梯度算法得到的最优可行解的目标值为10，这明显不是最优解（最优解应该是16，$x_1=1$，其余变量为0）
这是因为我们松弛了一个约束，所以通过拉格朗日松弛&次梯度算法得到的解不一定是最优解。但是当遇到一些很难求解的模型，但又不需要去求解它的精确解时，拉格朗日松弛&次梯度算法就可以派上用场了！

参考链接：

• 【凸优化笔记5】-次梯度方法（Subgradient method）
• 运筹学教学|快醒醒，你的熟人拉格朗日又来了！！
• 拉格朗日松弛求解整数规划浅析（附Python代码实例）

来源地址：https://blog.csdn.net/weixin_51545953/article/details/129281753