【数据结构】选择排序 & 堆排序（二）

目录

一，选择排序

1，基本思想

2， 基本思路

3，思路实现

二，堆排序

1，直接选择排序的特性总结：

2，思路实现

3，源代码

最后祝大家国庆快乐！

一，选择排序

1，基本思想

每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始（末尾）位置，直到全部待排序的数据元素排完 。

2， 基本思路

1，在元素集合 array[ i ] -- array[ n-1 ] 中选择关键码最大(小)的数据元素

2，若它不是这组元素中的最后一个(第一个)元素，则将它与这组元素中的最后一个（第一个）元素交换

3，在剩余的 array[ i ] -- array[ n-2 ]（array [ i+1] -- array [ n-1 ] ）集合中，重复上述步骤，直到集合剩余1个元素

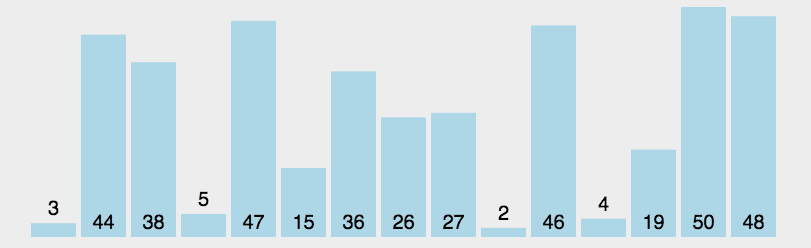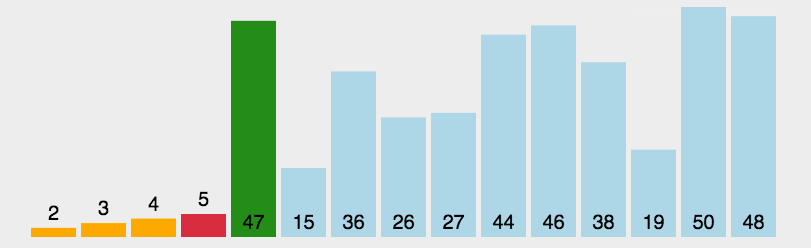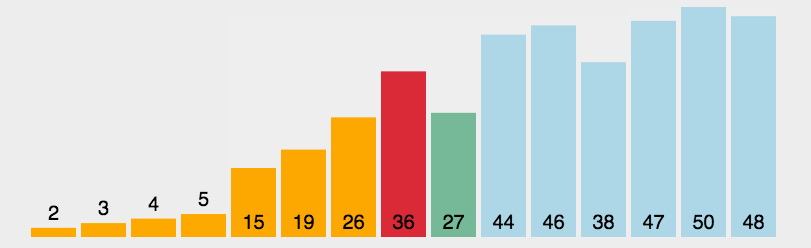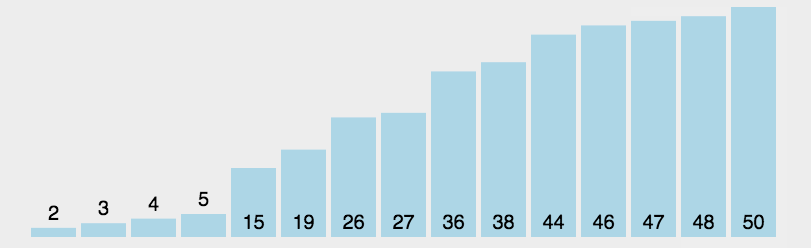
直接选择排序的特性总结：

直接选择排序思考非常好理解，但是效率不是很好。实际中很少使用

时间复杂度：O(N^2)

空间复杂度：O(1)

稳定性：不稳定

3，思路实现

选择排序嘛，就是先遍历数组找出最大数和最小数，然后让最小数与首元素交换，最大数与末尾元素交换，当然啦在排序的过程中与之交换的 " 首元素 " 和 " 末尾元素 " 会一直变化的；

第一趟排序时，首元素是 arr [ 0 ] ，末尾元素是 arr [ n-1 ] ；

第二趟排序时，首元素是 arr [ 1 ] ，末尾元素是 arr [ n-2 ] ；

。。。。。

以此类推直至首元素的小标大于或等于末尾元素的下标；

我们现在写一个升序的选择排序：

//选择排序void SeleSort(int* arr, int n){int begin = 0, end = n - 1;while (begin < end){int maxi = begin, mini = begin;for (int i = begin; i <= end; i++){if (arr[i] > arr[maxi]){maxi = i;}if (arr[i] < arr[mini]){mini = i;}}Swap(&arr[begin], &arr[mini]);// 如果maxi和begin重叠，修正一下即可if (begin == maxi){maxi = mini;}Swap(&arr[end], &arr[maxi]);++begin;--end;}}

我们测试一下：

int main(){int arr[] = { 9,1,2,5,7,4,8,6,3,5 };//选择排序SeleSort(arr, sizeof(arr) / sizeof(arr[0]));PrintSort(arr, sizeof(arr) / sizeof(arr[0]));return 0;}

可以看到是有序的，选择排序就 OK 了；

二，堆排序

堆排序(Heapsort)是指利用堆积树（堆）这种数据结构所设计的一种排序算法，它是选择排序的一种。它是通过堆来进行选择数据。需要注意的是排升序要建大堆，排降序建小堆。

1，直接选择排序的特性总结：

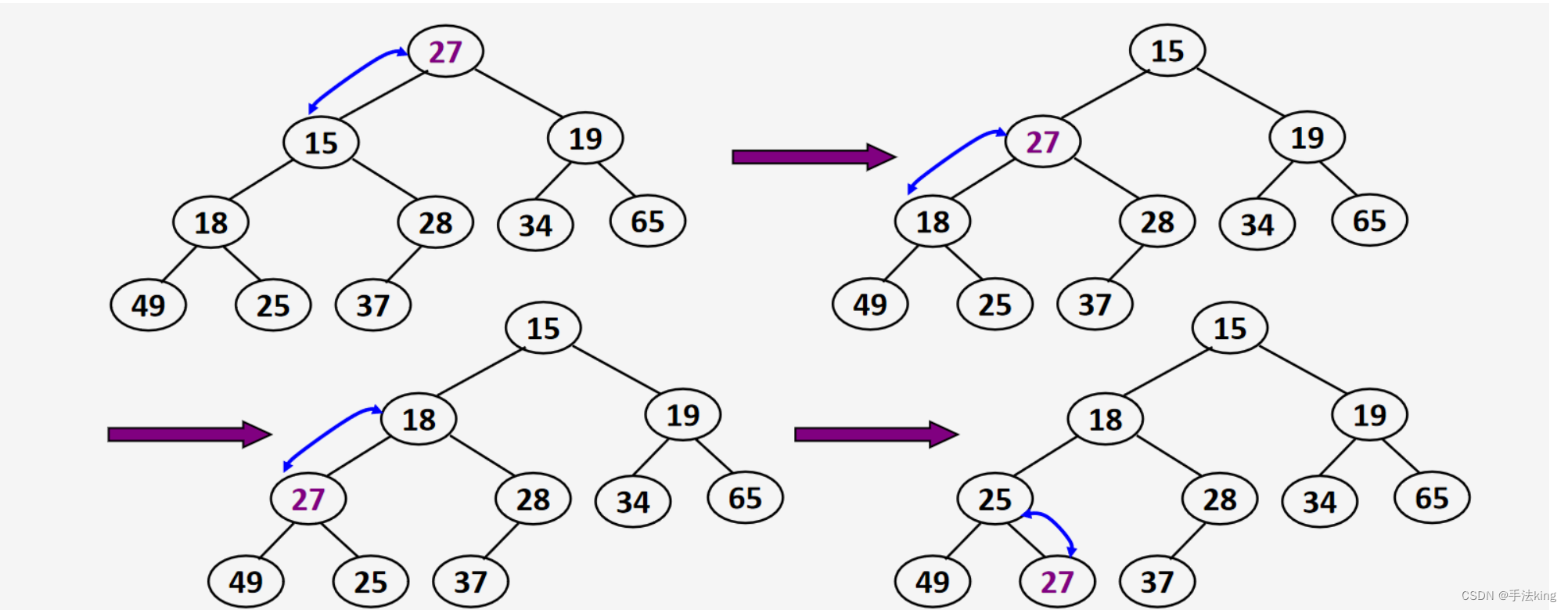
1， 堆排序使用堆来选数，效率就高了很多。

2， 时间复杂度：O(N*logN)

，空间复杂度：O(1)

，稳定性：不稳定

2，思路实现

要使用堆排序，首先就是要建堆，建堆有两种方式，一种是向上建堆法，一种是向下建堆法；

向上调整建堆的时间复杂度为O(N*logN);

向下调整建堆的时间复杂度为O(N);

所以我们用向下建堆法：

//向下调整void DownAdjust(int* arr, int n, int i){int perent = i;int child = perent* 2 + 1;while (child arr[child]){child++;}if (arr[perent] < arr[child]){//交换Swap(&arr[perent], &arr[child]);perent = child;child = perent * 2 + 1;}else{break;}}}//建堆int i = 0;for (i = (n - 1 - 1) / 2; i >= 0; i--){//向下调整DownAdjust(arr, n, i);}

此时堆就建好了，然后就是用【交换删除法】来排序了：

原理：

此时堆顶是最大的数据，让其与末尾的数进行交换，然后让 n--，在让其向下调整这样就可以避开末尾的数了，以此类推直至 n<=1 ，排序就排好了；

//交换，删除排序法while (n > 1){//交换Swap(&arr[0], &arr[n - 1]);n--;//向下调整DownAdjust(arr, n, 0);}

我们测试一下：

int main(){int arr[] = { 9,1,2,5,7,4,8,6,3,5 };//堆排序HeapSort(arr, sizeof(arr) / sizeof(arr[0]));PrintSort(arr, sizeof(arr) / sizeof(arr[0]));return 0;}

可以看到是有序的，堆排序就 OK 了；

3，源代码

//向下调整void DownAdjust(int* arr, int n, int i){int perent = i;int child = perent* 2 + 1;while (child arr[child]){child++;}if (arr[perent] < arr[child]){//交换Swap(&arr[perent], &arr[child]);perent = child;child = perent * 2 + 1;}else{break;}}}//堆排序void HeapSort(int* arr, int n){//建堆int i = 0;for (i = (n - 1 - 1) / 2; i >= 0; i--){//向下调整DownAdjust(arr, n, i);}//交换，删除排序法while (n > 1){//交换Swap(&arr[0], &arr[n - 1]);n--;//向下调整DownAdjust(arr, n, 0);}}

第二阶段就到这里了，带大家在秒杀两个排序松松骨，真正有挑战的排序还在后头！

后面博主会陆续更新；

如有不足之处欢迎来补充交流！

完结。。

最后祝大家国庆快乐！

来源地址：https://blog.csdn.net/m0_71676870/article/details/133465270