文章目录 前言什么是前缀和算法1.【模板】前缀和1.1 题目要求1.2 做题思路1.3 Java代码实现 2. 【模板】二维前缀和2.1 题目要求2.2 做题思路2.3 Java代码实现

前缀和算法是一种常用的优化技术,用于加速某些涉及连续子数组或子序列求和的问题。它基于一个简单但强大的思想,通过提前计算并存储数组的前缀和,以便在后续查询中可以快速获取任意区间的和。
在许多算法问题中,我们需要频繁地查询子数组的和,例如最大子数组和、连续子数组的平均值等。传统的方法是在每次查询时遍历数组,并计算所需区间的和,这样会导致时间复杂度较高。
而前缀和算法通过预处理数组,计算出每个位置的前缀和,并将其保存在一个额外的数组中。这样,在查询时,我们只需要简单地减去两个前缀和即可得到所需子数组的和,从而将查询时间降低为O(1)的常数复杂度。
前缀和算法(Prefix Sum AlGorithm)是一种用于高效计算数组前缀和的算法。前缀和是指数组中某个位置之前(包括该位置)所有元素的和。
前缀和算法的基本思想是通过一次遍历数组,计算每个位置的前缀和,并将其存储在一个新的数组中。然后,可以通过查询新数组中的元素,快速计算出任意子数组的和。
具体步骤如下:
通过前缀和算法,可以在O(1)的时间复杂度内计算出任意子数组的和。例如,要计算原数组中从位置i到位置j的子数组和,只需计算prefixSum[j] - prefixSum[i-1]即可。如果i为0,则直接返回prefixSum[j]。
前缀和算法在解决一些与子数组和相关的问题时非常有用,例如求解子数组和等于目标值的个数、求解最大子数组和、求解最长连续子数组和等。
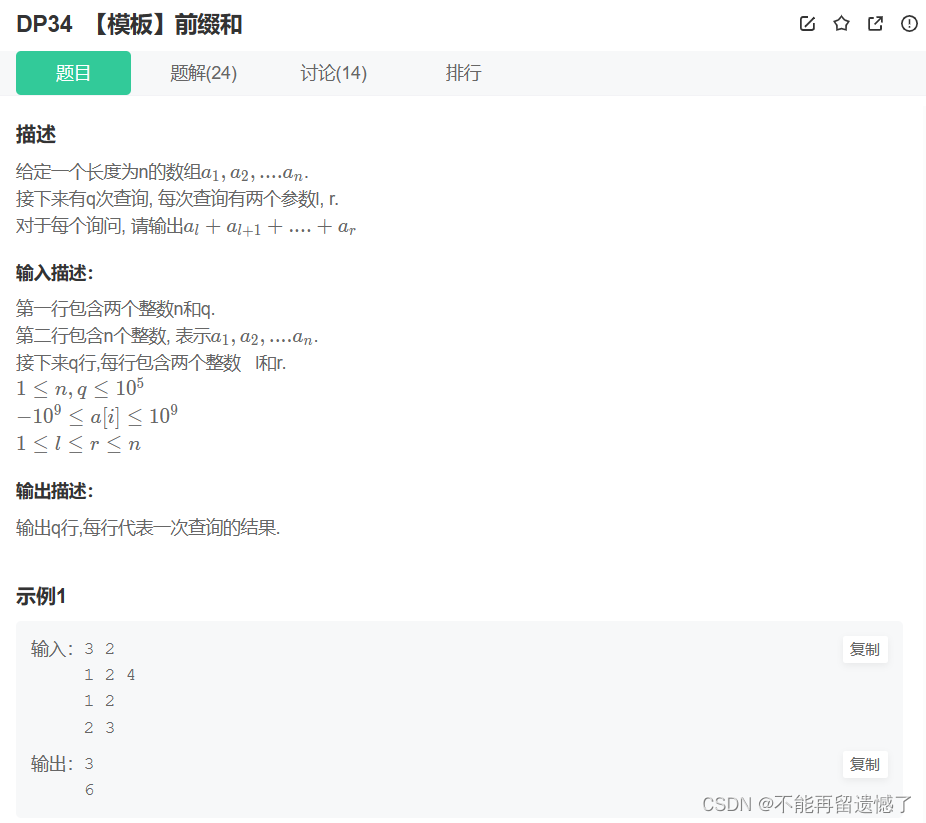
import java.util.Scanner;// 注意类名必须为 Main, 不要有任何 package xxx 信息public class Main { public static void main(String[] args) { Scanner in = new Scanner(System.in); // 注意 hasNext 和 hasNextLine 的区别 while (in.hasNextInt()) { // 注意 while 处理多个 case int a = in.nextInt(); int b = in.nextInt(); System.out.println(a + b); } }}按照暴力解法的思路,每次查询 l 到 r 之间的和的时候,就需要遍历一次数组,那么这样的时间复杂度就是 O(q*n) 了,因为进行了较多的重复计算,导致时间效率较低,那么是否有一种方法可以减少重复计算呢?答案是有的,这就是前缀和的思路,其实有点类似于前面我为大家分享的滑动窗口中进窗口的操作,每次进窗口更新数据的时候只需要用前面已经计算了的数字的和加上进窗口的那个数据,就得到了当前位置之前所有元素的和。通过这样的思路就大大减少了重复计算。
然后这个求 l 到 r 之间元素的和的时候,就只需要用 r 和 r 之前所有元素的和减去 l 之前所有元素的和就可以了。
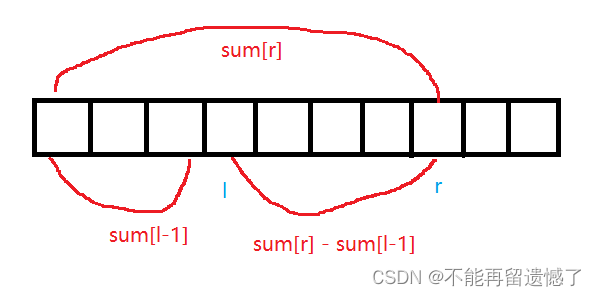
并且仔细的人可能会发现:为什么 l 和 r 都是从1开始而不是0呢?因为从下标为0开始的话,就需要求0 ~ -1 之间元素的和,但是这个区间是不合法的,所以数组从 1 开始就可以防止出现这种的情况。
在开始求 l 到 r 之间元素的和的时候,可以先对数组进行一个预处理,求出数组中每个位置之前的前缀和。
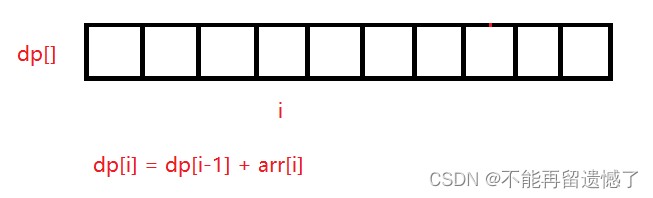
import java.util.Scanner;// 注意类名必须为 Main, 不要有任何 package xxx 信息public class Main { public static void main(String[] args) { Scanner in = new Scanner(System.in); // 注意 hasNext 和 hasNextLine 的区别 while (in.hasNextInt()) { // 注意 while 处理多个 case int n = in.nextInt(),q = in.nextInt(); int[] arr = new int[n + 1]; for(int i = 1; i <= n; i++) arr[i] = in.nextInt(); //创建一个同样大小的前缀和数组,并且因为是多个元素的和, //可能会超出int所能表示的最大范围,这里用long来表示 long[] dp = new long[n + 1]; for(int i = 1; i <= n; i++) { dp[i] = dp[i-1] + arr[i]; } for(int i = 0; i < q; i++) { int l = in.nextInt(),r = in.nextInt(); System.out.println(dp[r] - dp[l-1]); } } }}

import java.util.Scanner;// 注意类名必须为 Main, 不要有任何 package xxx 信息public class Main { public static void main(String[] args) { Scanner in = new Scanner(System.in); // 注意 hasNext 和 hasNextLine 的区别 while (in.hasNextInt()) { // 注意 while 处理多个 case int a = in.nextInt(); int b = in.nextInt(); System.out.println(a + b); } }}二维前缀和和一维前缀和的思路基本上相同的,只是一个是一维数组,一个是二维数组,一些处理细节不同。
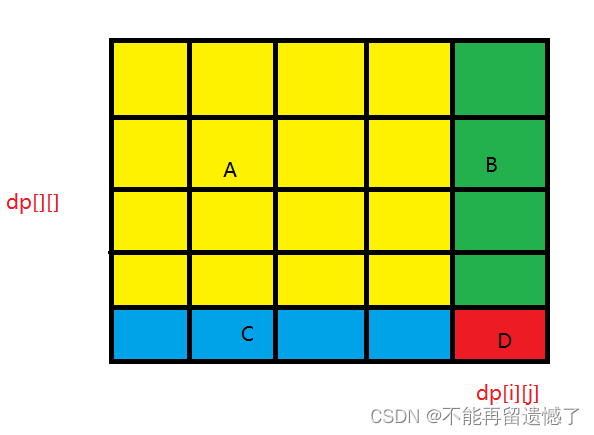
当求 dp[i][j] 的时候,可以将 dp 数组分成 A、B、C、D 四个部分,A 部分是从 0,0 位置开始到 i - 1,j - 1 位置之间的矩阵元素的和。dp[i][j] = A + B + C + D 之间的元素的和,但是这里 B 和 C 区间之间的元素不是很容易求和,所以我们可以用
(A + B) + (A + C) + D - A 来求 dp[i][j] 的值。
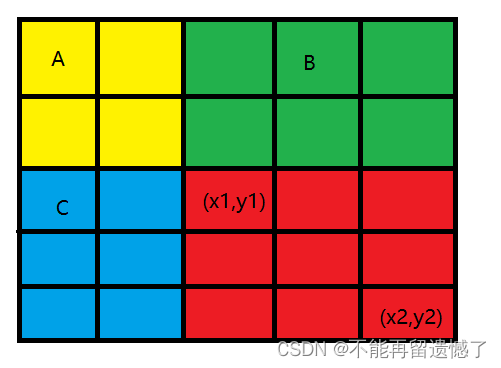
然后(x1,y1) 到 (x2,y2)之间的矩阵的和,我们可以使用 dp[x2][y2] - (A + B) - (A + C) + A,也就是 dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1]。
import java.util.Scanner;// 注意类名必须为 Main, 不要有任何 package xxx 信息public class Main { public static void main(String[] args) { Scanner in = new Scanner(System.in); // 注意 hasNext 和 hasNextLine 的区别 while (in.hasNextInt()) { // 注意 while 处理多个 case int n = in.nextInt(),m = in.nextInt(),q = in.nextInt(); int[][] arr = new int[n + 1][m + 1]; for(int i = 1; i <= n; i++) { for(int j = 1; j <= m; j++) { arr[i][j] = in.nextInt(); } } //构造二维前缀和数组 long[][] dp = new long[n + 1][m + 1]; for(int i = 1; i <= n; i++) { for(int j = 1; j <= m; j++) { dp[i][j] = dp[i - 1][j] + dp[i][j - 1] + arr[i][j] - dp[i - 1][j - 1]; } } for(int i = 0; i < q; i++) { int x1 = in.nextInt(),y1 = in.nextInt(),x2 = in.nextInt(),y2 = in.nextInt(); System.out.println(dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1 - 1][y1 - 1]); } } }}
https://leetcode.cn/problems/find-pivot-index/description/
给你一个整数数组 nums ,请计算数组的 中心下标 。
数组 中心下标 是数组的一个下标,其左侧所有元素相加的和等于右侧所有元素相加的和。
如果中心下标位于数组最左端,那么左侧数之和视为 0 ,因为在下标的左侧不存在元素。这一点对于中心下标位于数组最右端同样适用。
如果数组有多个中心下标,应该返回 最靠近左边 的那一个。如果数组不存在中心下标,返回 -1 。
示例 1:
输入:nums = [1, 7, 3, 6, 5, 6]输出:3解释:中心下标是 3 。左侧数之和 sum = nums[0] + nums[1] + nums[2] = 1 + 7 + 3 = 11 ,右侧数之和 sum = nums[4] + nums[5] = 5 + 6 = 11 ,二者相等。示例 2:
输入:nums = [1, 2, 3]输出:-1解释:数组中不存在满足此条件的中心下标。示例 3:
输入:nums = [2, 1, -1]输出:0解释:中心下标是 0 。左侧数之和 sum = 0 ,(下标 0 左侧不存在元素),右侧数之和 sum = nums[1] + nums[2] = 1 + -1 = 0 。提示:
class Solution { public int pivotIndex(int[] nums) { }}这个题目要求我们找到一个元素,这个元素的左边所有元素的和等于该元素右边所有元素的和,通过前面的两个题目我们做这道题目应该是会有一点思路的。
因为要求的是某一元素左边部分和前面部分的元素的和,所以我们可以使用两个数组,分别记录数组中每一个元素的前缀和以及后缀和,前缀和数组从前往后插入数据,后缀和数组从后往前插入数据,并且前缀和的第一个数据为0,后缀和的最后一个数据为0。最后再遍历一次数组,判断数组某一位置的前缀和是否等于后缀和。
class Solution { public int pivotIndex(int[] nums) { int n = nums.length; int[] f = new int[n]; //前缀和数组 int[] g = new int[n]; //后缀和数组 for(int i = 1; i < n; i++) { f[i] = f[i-1] + nums[i - 1]; } for(int i = n - 2; i >= 0; i--) { g[i] = g[i + 1] + nums[i + 1]; } for(int i = 0; i < n; i++) { if(f[i] == g[i]) return i; } return -1; }}
https://leetcode.cn/problems/product-of-array-except-self/
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。
题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。
请不要使用除法,且在 O(n) 时间复杂度内完成此题。
示例 1:
输入: nums = [1,2,3,4]输出: [24,12,8,6]示例 2:
输入: nums = [-1,1,0,-3,3]输出: [0,0,9,0,0]提示:
class Solution { public int[] productExceptSelf(int[] nums) { }}这个题目跟上面的 寻找数组的中心下标 思路基本上差不多,只是判断前缀和和后缀和相等的操作换成了前缀积和后缀积的乘积,这里我就不过多介绍了,大家可以直接看代码。
class Solution { public int[] productExceptSelf(int[] nums) { int n = nums.length; int[] f = new int[n]; int[] g = new int[n]; //这里需要注意前缀积的第一个元素和后缀积的最后一个元素要初始化为1,因为是乘法 f[0] = 1; g[n-1] = 1; for(int i = 1; i < n; i++) { f[i] = f[i - 1] * nums[i - 1]; } for(int i = n-2; i >= 0; i--) { g[i] = g[i + 1] * nums[i + 1]; } int[] ret = new int[n]; for(int i = 0; i < n; i++) { ret[i] = f[i] * g[i]; } return ret; }}
https://leetcode.cn/problems/subarray-sum-equals-k/description/
给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k 的连续子数组的个数 。
示例 1:
输入:nums = [1,1,1], k = 2输出:2示例 2:
输入:nums = [1,2,3], k = 3输出:2提示:
class Solution { public int subarraySum(int[] nums, int k) { }}还是先来看看暴力解法是怎样解决的?遍历数组,以数组的每一元素为起始位置,然后看以该元素为起始位置的子数组是否和为 k ,暴力解法的时间复杂度为 O(N*2)。
很多人看到这个题目首先想到的可能是 滑动窗口 ,但是我们需要仔细看题目,使用滑动窗口,需要保证窗口具有单调性,这里题目没有说数组全为非负数或者非整数,所以不能保证窗口的单调性,不能使用滑动窗口。
换个思路,它既然求的是和为 k 的子数组,我们仍然可以使用前缀和的思想,在数组的某个位置之前找到 该位置的前缀和 - k = 该位置之前的某一位置的前缀和,并且这个题目求的是 子数组的个数,我们可以配合着哈希表来进行计数。哈希表中存储的是某一位置的前缀和以及该前缀和出现的次数。
与暴力解法的思路有些许的区别,在构建前缀和数组的时候,我们不以数组中每个元素作为起始位置,而是将每个元素作为结束位置,这样更贴合我们的前缀和思想。

class Solution { public int subarraySum(int[] nums, int k) { Map<Integer,Integer> map = new HashMap<>(); //为了防止从0开始到某一位置的子数组的和为k,所以提前放入一个前缀和为0的键值对 map.put(0,1); int n = nums.length; int ret = 0,sum = 0; for(int i = 0; i < n; i++) { sum += nums[i]; ret += map.getOrDefault(sum-k,0); map.put(sum,map.getOrDefault(sum,0) + 1); } return ret; }}
https://leetcode.cn/problems/subarray-sums-divisible-by-k/description/
给定一个整数数组 nums 和一个整数 k ,返回其中元素之和可被 k 整除的(连续、非空) 子数组 的数目。
子数组 是数组的 连续 部分。
示例 1:
输入:nums = [4,5,0,-2,-3,1], k = 5输出:7解释:有 7 个子数组满足其元素之和可被 k = 5 整除:[4, 5, 0, -2, -3, 1], [5], [5, 0], [5, 0, -2, -3], [0], [0, -2, -3], [-2, -3]示例 2:
输入: nums = [5], k = 9输出: 0提示:
class Solution { public int subarraysDivByK(int[] nums, int k) { }}在做这个题目之前,我们需要知道两个额外的知识点:

当知道这两个定理之后,那么这个题目的思路就跟上面的 和为 k 的子数组 思路是类似的。
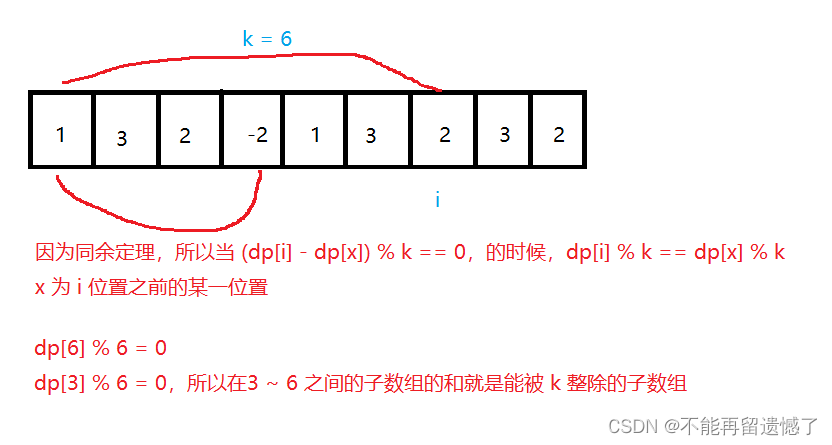
class Solution { public int subarraysDivByK(int[] nums, int k) { Map<Integer,Integer> map = new HashMap<>(); //同样为了防止从0开始到某一位置的子数组的乘积都能被k整除 map.put(0 % k,1); int n = nums.length; int sum = 0,ret = 0; for(int i = 0; i < n; i++) { sum += nums[i]; int r = (sum % k + k) % k; ret += map.getOrDefault(r,0); map.put(r,map.getOrDefault(r,0) + 1); } return ret; }}
https://leetcode.cn/problems/contiguous-array/description/
给定一个二进制数组 nums , 找到含有相同数量的 0 和 1 的最长连续子数组,并返回该子数组的长度。
示例 1:
输入: nums = [0,1]输出: 2说明: [0, 1] 是具有相同数量 0 和 1 的最长连续子数组。示例 2:
输入: nums = [0,1,0]输出: 2说明: [0, 1] (或 [1, 0]) 是具有相同数量0和1的最长连续子数组。提示:
class Solution { public int findMaxLength(int[] nums) { }}因为数组中只有二进制数,也就是0和1,我们可以将0当成是-1,当子数组中0和1的数量相同的时候,子数组的和为0。所以这个题目也就相当于求长度最长的和为0的子数组。所以我们哈希表中存储的就是前缀和以及数组的下标。
class Solution { public int findMaxLength(int[] nums) { Map<Integer,Integer> map = new HashMap<>(); map.put(0,-1); int n = nums.length; int ret = 0,sum = 0; for(int i = 0; i < n; i++) { sum += (nums[i] == 0 ? -1 : 1); if(map.containsKey(sum)) ret = Math.max(ret,i-map.getOrDefault(sum,0)); else map.put(sum,i); } return ret; }}
https://leetcode.cn/problems/matrix-block-sum/description/
给你一个 m x n 的矩阵 mat 和一个整数 k ,请你返回一个矩阵 answer ,其中每个 answer[i][j] 是所有满足下述条件的元素 mat[r][c] 的和:
示例 1:
输入:mat = [[1,2,3],[4,5,6],[7,8,9]], k = 1输出:[[12,21,16],[27,45,33],[24,39,28]]示例 2:
输入:mat = [[1,2,3],[4,5,6],[7,8,9]], k = 2输出:[[45,45,45],[45,45,45],[45,45,45]]提示:
class Solution { public int[][] matrixBlockSum(int[][] mat, int k) { }}这个题目跟上面的【模板】二维前缀和是类似的,只是这个题目需要我们找到对应的矩阵。
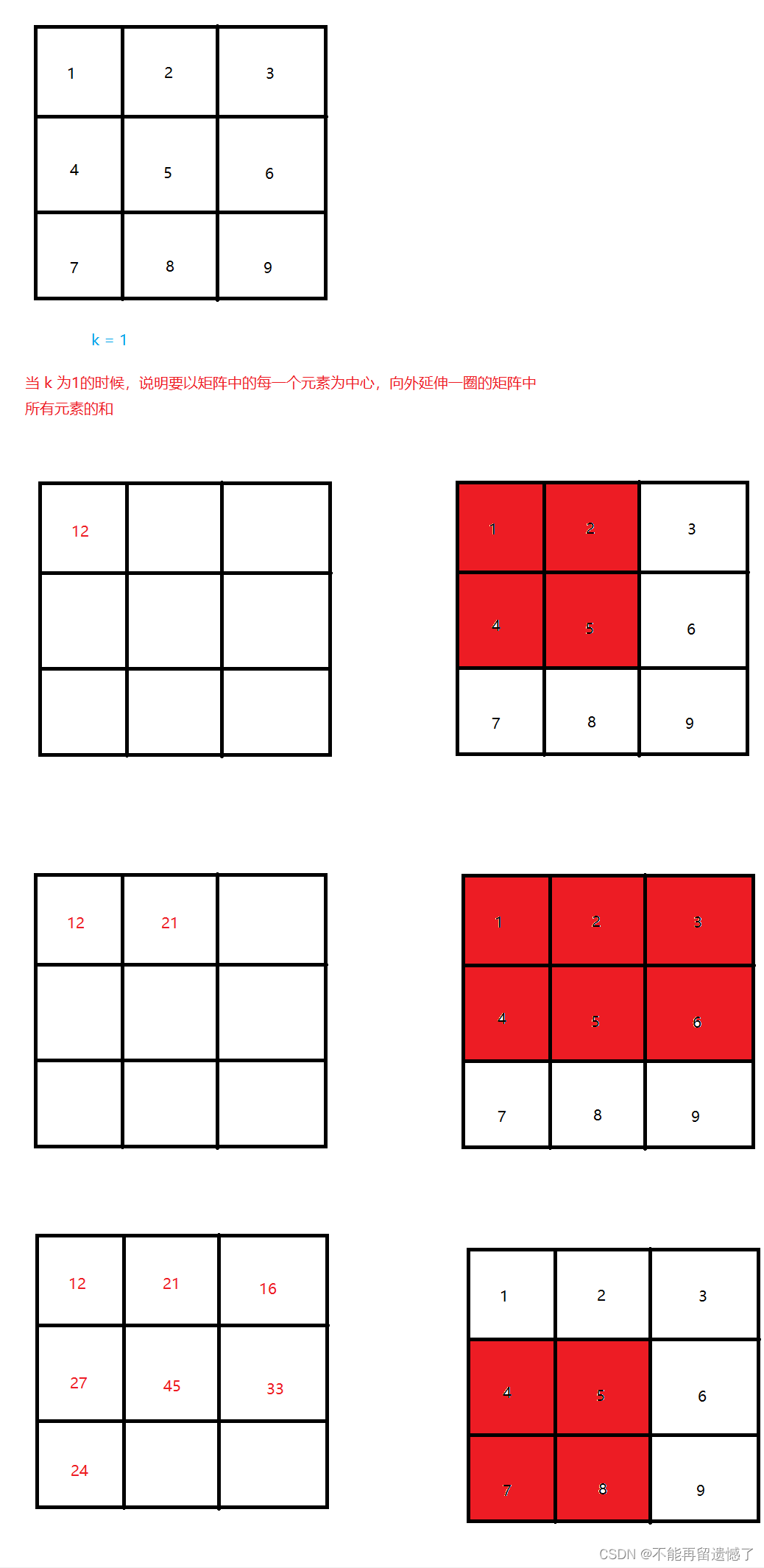
需要注意的是,题目中的 r 和 c 都是从0开始的,也就是说,可能会出现数组越界的情况,这道题题目的重点就是需要处理下标越界的情况。那么如何处理下标越界的情况呢?很简单,前面的不是有从下标1开始的吗?当我们构建前缀和数组的时候,我们也可以将数组下标以1开始,然后在最终结果的数组中填入数据的时候注意下标的映射关系就行了。
class Solution { public int[][] matrixBlockSum(int[][] mat, int k) { int n = mat.length; int m = mat[0].length; int[][] dp = new int[n + 1][m + 1]; for(int i = 1; i <= n; i++) { for(int j = 1; j <= m; j++) { dp[i][j] = dp[i - 1][j] + dp[i][j - 1] + mat[i - 1][j - 1] - dp[i - 1][j - 1]; } } int[][] ret = new int[n][m]; for(int i = 0; i < n; i++) { for(int j = 0; j < m; j++) { //处理下标越界问题,并且解决了下标的映射关系 int x1 = Math.max(0,i-k) + 1,y1 = Math.max(0,j - k) + 1; int x2 = Math.min(n - 1,i + k) + 1,y2 = Math.min(m - 1,j + k) + 1; ret[i][j] = dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 - 1]; } } return ret; }}
通过前缀和算法,我们可以在O(1)的时间复杂度内计算出任意区间的元素和。这在处理大规模数据时非常有用,可以大大提高计算效率。
总结起来,前缀和算法是一种高效计算数组区间和的方法。它通过计算数组的前缀和,可以在O(1)的时间复杂度内得到任意区间的元素和。在实际应用中,前缀和算法经常用于解决数组区间和相关的问题,例如子数组的最大和、子数组的平均值等。通过掌握前缀和算法,我们可以更加高效地解决这类问题。
来源地址:https://blog.csdn.net/m0_73888323/article/details/132511286
--结束END--
本文标题: 【算法系列篇】前缀和
本文链接: https://lsjlt.com/news/402391.html(转载时请注明来源链接)
有问题或投稿请发送至: 邮箱/279061341@qq.com QQ/279061341
2024-04-01
2024-04-03
2024-04-03
2024-01-21
2024-01-21
2024-01-21
2024-01-21
2023-12-23
回答
回答
回答
回答
回答
回答
回答
回答
回答
回答
0