C++二叉搜索树BSTree如何使用

这篇文章主要介绍“c++二叉搜索树BSTree如何使用”的相关知识，小编通过实际案例向大家展示操作过程，操作方法简单快捷，实用性强，希望这篇“C++二叉搜索树BSTree如何使用”文章能帮助大家解决问题。

一、概念

二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树:

若它的左子树不为空，则左子树上所有节点的值都小于根节点的值

若它的右子树不为空，则右子树上所有节点的值都大于根节点的值

左<根<右

它的左右子树也分别为二叉搜索树

之所以又叫二叉排序树，是因为二叉搜索树中序遍历的结果是有序的

二、基础操作

1.查找find

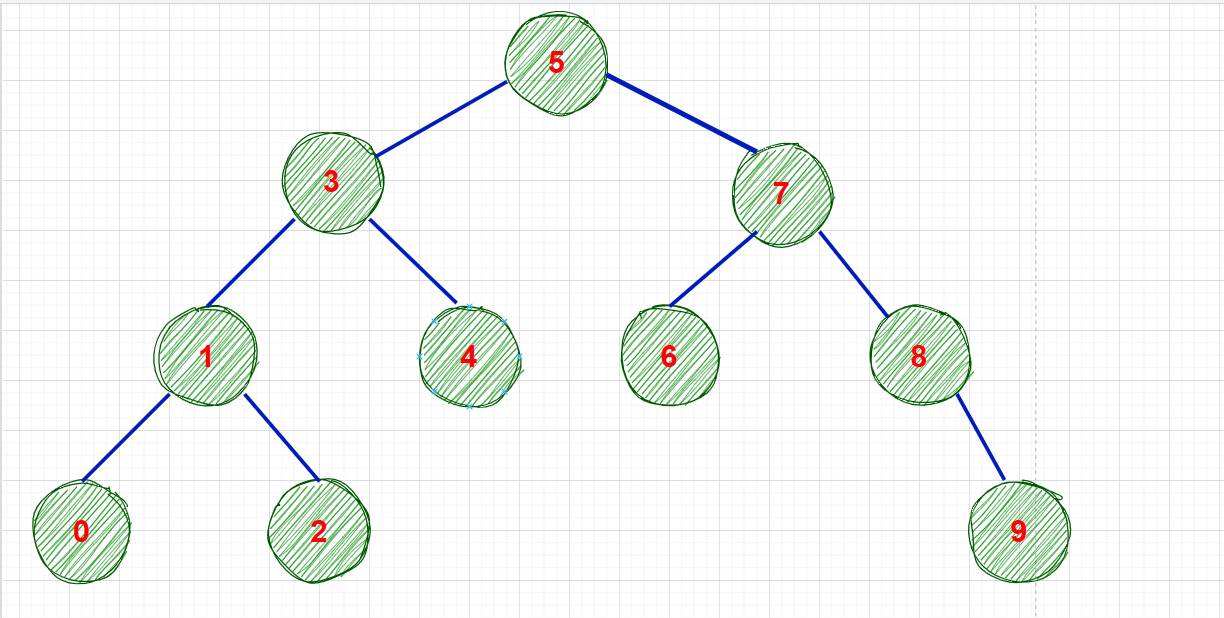
基于二叉搜索树的特点，查找一个数并不难，若根节点不为空的情况下：

若根节点key==查找key，直接返回true

若根节点key>查找key，那得找到更小的，则往左子树查找

若根节点key<查找key，那得找到更大的，则往右子树查找

最多查找高度次，走到空为止，如果还没找到，则说明这个值不存在，返回false

bool find(const K& key){node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return true;}}return false;}

2.插入Insert

树为空，则直接插入,新增节点，直接插入root指针即可

树不为空，按二叉搜索树性质查找插入位置，插入新节点。

（注意：不能插入重复的元素，并且每次插入都是要定位到空节点的位置；我们先定义一个 cur从root开始，比较元素的大小：若插入的元素比当前位置元素小就往左走，比当前位置元素大就往右走，直到为空,相等就不能插入了;同时定义一个parent去记录当前 cur的前一个位置，最后判断cur是parent的左子树还是右子树即可）

bool Insert(const K& key){if (_root == nullptr){_root = new Node(key);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(key);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}

3.中序遍历InOrder

递归走起，同时由于_root是私有的，外部不能访问，我们可以在类内给中序提供一个方法即可，就不需要传参了

void InOrder(){_InOrder(_root);cout << endl;}private:void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}Node* _root = nullptr;

4.删除erase

删除的情况比较多：

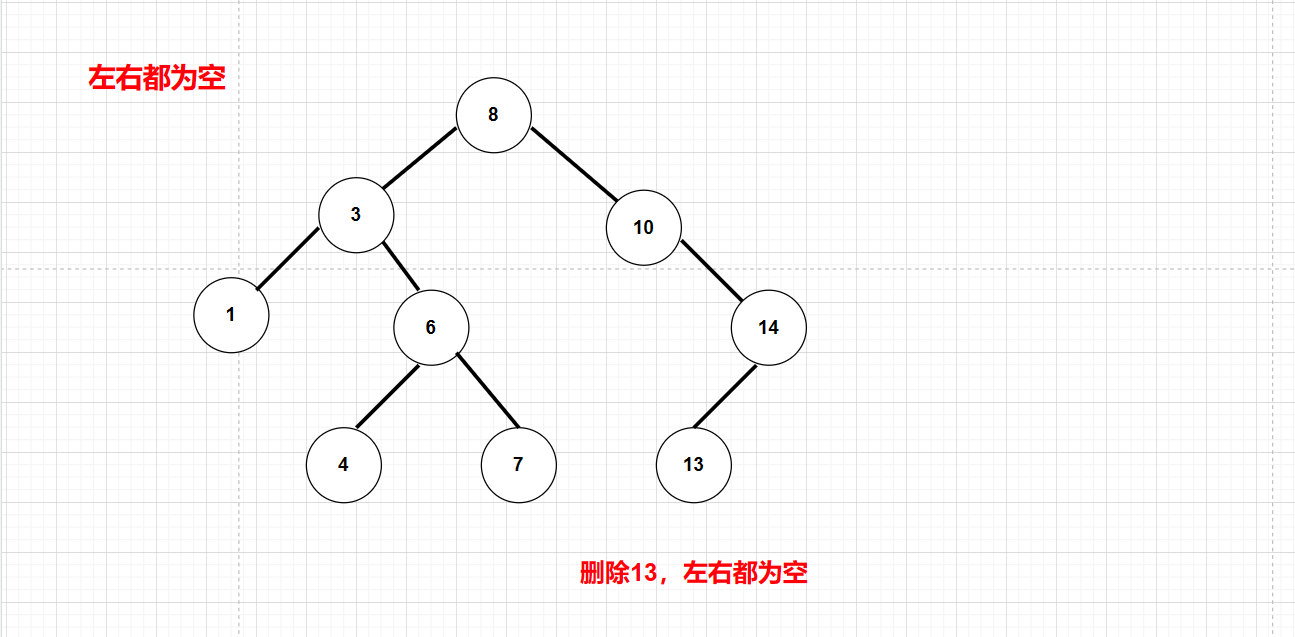
• 左右都为空：叶子结点，直接置空并链接到空指针

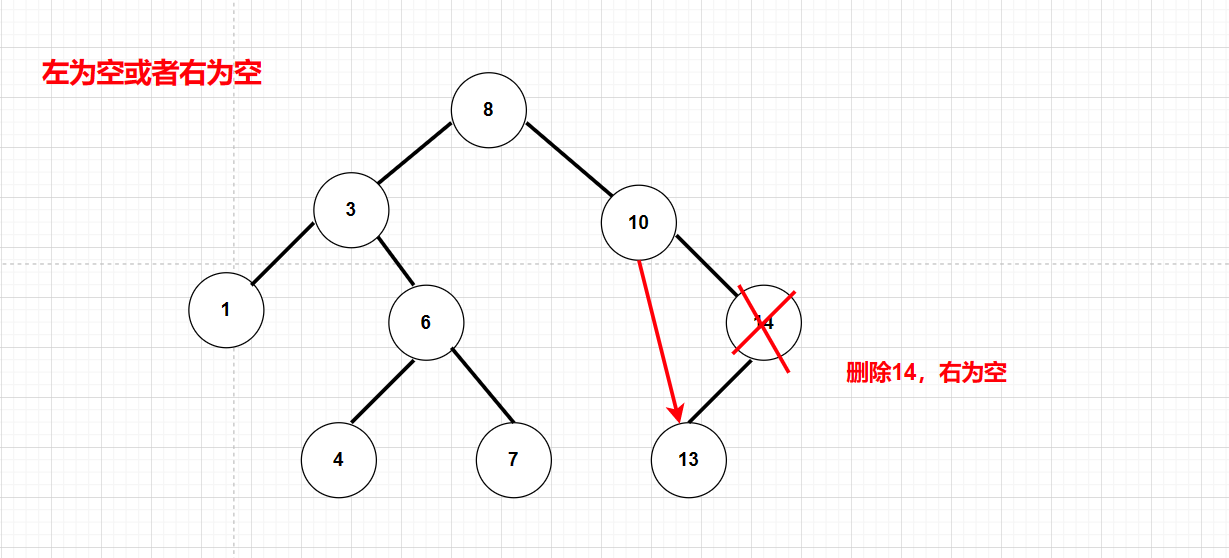
• 左为空或右为空：进行托孤：只有一个子节点，删除自己本身，并链接子节点和父节点（注意：如果父亲是空，也就是要删除根结点，此时根节点没有父亲，单独判断一下）

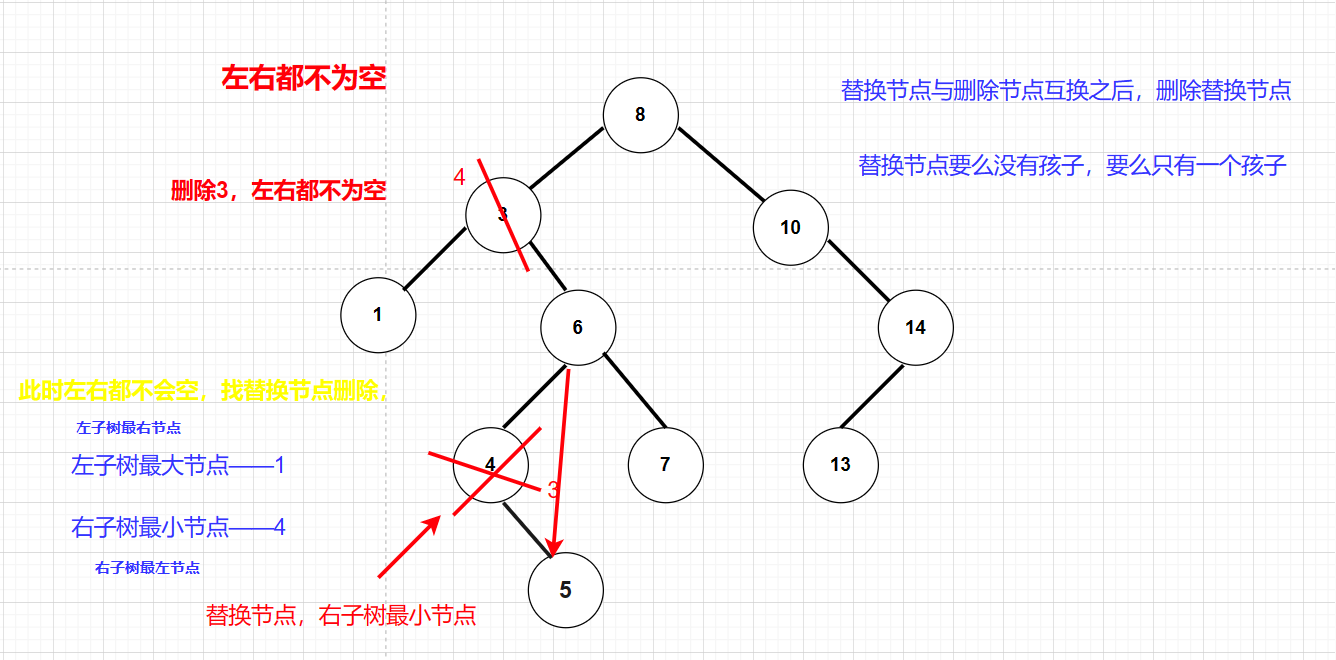
• 左右都不为空：找出替换节点：右子树最小节点**、**左子树最大节点。替换节点可以作为交换和删除进行交换，交换后删除交换节点、交换节点要么没有孩子，要么只有一个孩子可以直接删除

但是左右都为空可以纳入到左为空或右为空的情况

注意：

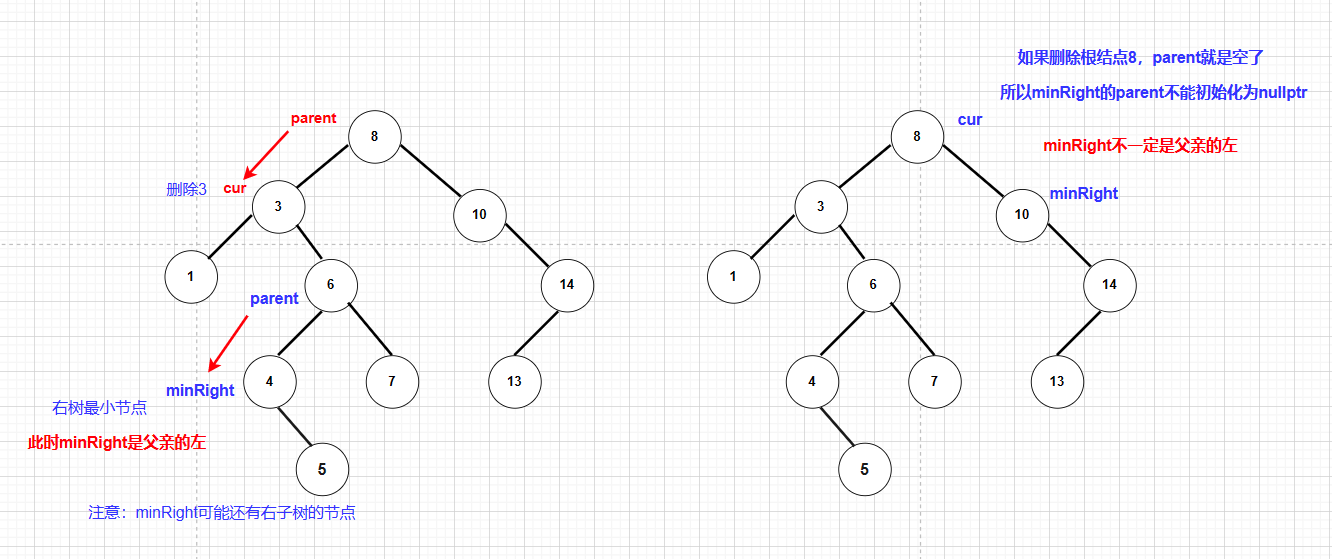
代码实现：

bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{//左为空if (cur->_left == nullptr){//删除根结点//if(parent==nullptr)if (cur == _root){_root = cur->_right;}else{if (parent->_left == cur){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}delete cur;}//右为空else if (cur->_right == nullptr){if (cur == _root){_root = cur->_left;}else{if (parent->_left == cur){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}delete cur;}//左右都不为空,找替换节点else{//不能初始化为nullptrNode* parent = cur;//右子树最小节点Node* minRight = cur->_right;while (minRight->_left){parent = minRight;minRight = minRight->_left;}cur->_key = minRight->_key;//判断minRight是父亲的左还是右if (minRight == parent->_left){parent->_left = minRight->_right;}else{parent->_right = minRight->_right;}delete minRight;}return true;}}return false;}

三、递归写法

1.递归查找

这个比较简单：苏醒把，递归时刻

bool _FindR(Node* root, const K& key){if (root == nullptr) return false;else if (root->_key < key) return _FindR(root->_right, key);else if (root->_key > key) return _FindR(root->_left, key);else return true;}

2.递归插入

最大的问题是插入之后跟父亲进行链接，如果直接给root是不可以的，因为root是栈帧里面的参数，只是局部变量：加上引用

bool _InsertR(Node*& root, const K& key){if (root == nullptr){root = new Node(key);return true;}else if (root->_key < key) return _InsertR(root->_right, key);else if (root->_key > key) return _InsertR(root->_left, key);else return false;}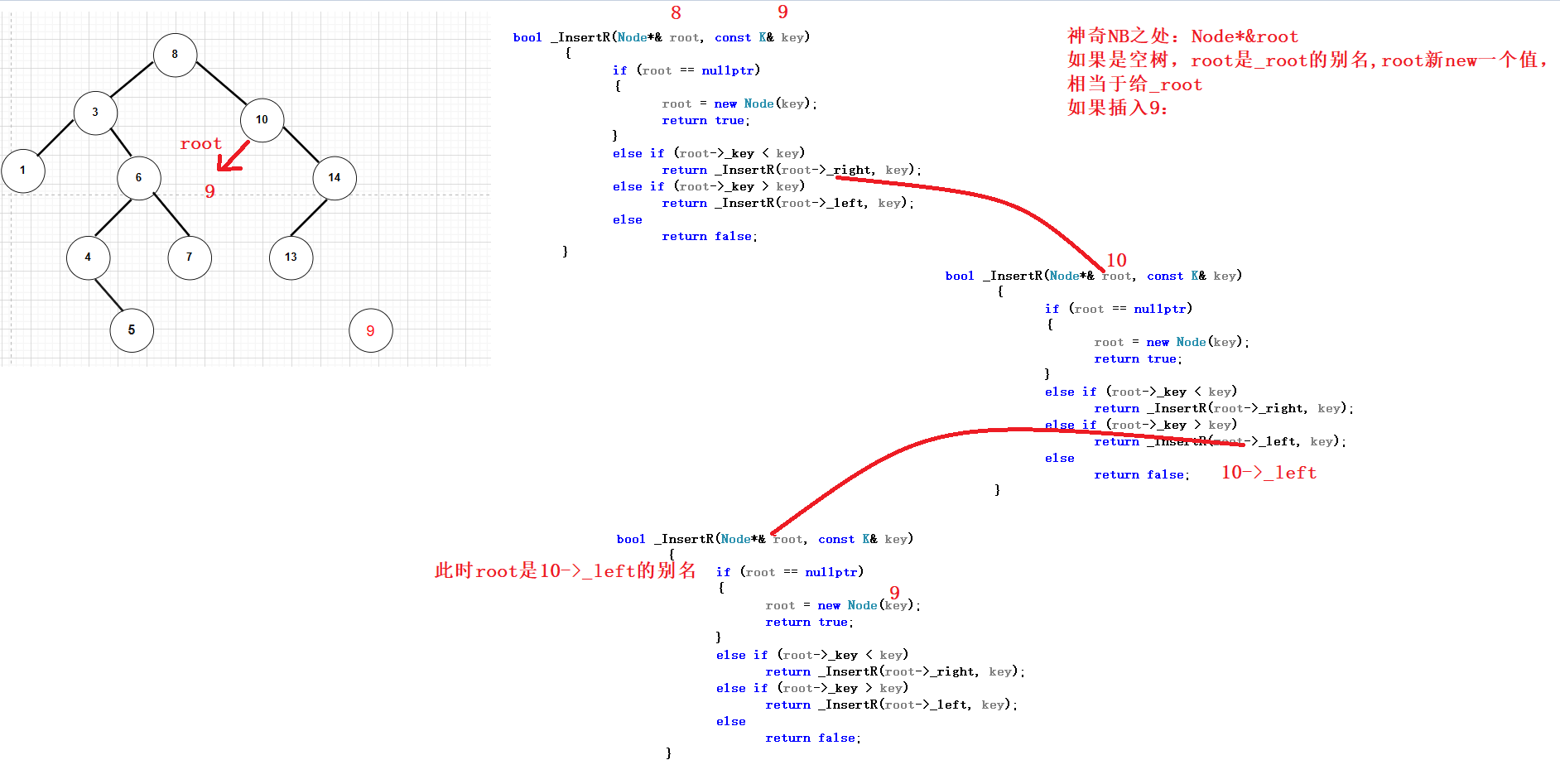

3.递归删除

递归删除怎么找到父节点？root = root->_left/ root = root->_right;

bool _EraseR(Node*& root, const K& key){if (root == nullptr){return false;}if (root->_key < key){return _EraseR(root->_right, key);}else if (root->_key > key){return _EraseR(root->_left, key);}else{Node* del = root;if (root->_right == nullptr){root = root->_left;}else if (root->_left == nullptr){root = root->_right;}else{Node* minRight = root->_right;while (minRight->_left){minRight = minRight->_left;}swap(root->_key, minRight->_key);return _EraseR(root->_right, key);}delete del;return true;}}

四、应用

最优情况下，二叉搜索树为完全二叉树，其平均比较次数为：log2N

最差情况下，二叉搜索树退化为单支树，其平均比较次数为： N/2

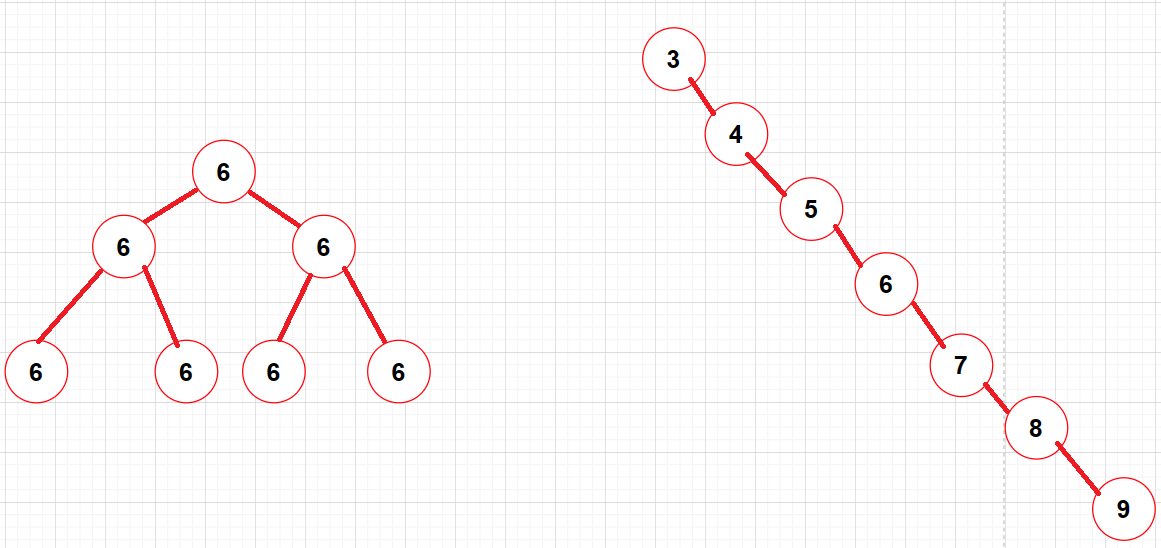
K模型：K模型即只有key作为关键码，结构中只需要存储Key即可，关键码即为需要搜索到的值，判断关键字是否存在。

比如：给一个单词Word，判断该单词是否拼写正确，具体方式如下：

以单词集合中的每个单词作为key，构建一棵二叉搜索树，在二叉搜索树中检索该单词是否存在，存在则拼写正确，不存在则拼写错误。

KV模型：每一个关键码key，都有与之对应的值Value，即**<Key, Value>**的键值对。

比如英汉词典就是英文与中文的对应关系，通过英文可以快速找到与其对应的中文，英文单词与其对应的中文<word, chinese>就构成一种键值对；再比如统计单词次数，统计成功后，给定单词就可快速找到其出现的次数，单词与其出现次数就是**<word, count>**就构成一种键值对。

namespace KV{template <class K,class V>struct BSTreeNode{BSTreeNode<K,V>* _left;BSTreeNode<K,V>* _right;K _key;V _value;BSTreeNode(const K& key,const V&value):_key(key),_value(value),_left(nullptr),_right(nullptr){}};template <class K,class V>class BSTree{        typedef BSTreeNode<K, V> Node;public:bool Insert(const K& key, const V& value)Node* find(const K& key)void InOrder()private:Node* _root = nullptr;};}void TestBSTree(){//key/Value的搜索模型；通过key查找或修改ValueKV::BSTree<string, string> dict;dict.Insert("sort", "排序");dict.Insert("string", "字符串");dict.Insert("left", "左");dict.Insert("right", "右");string str;while (cin >> str){KV::BSTreeNode<string, string>* ret = dict.find(str);if (ret){cout << ret->_value << endl;}else{cout << "找不到" << endl;}}}

源代码：

BSTree.h

#include <iOStream>using namespace std;namespace K{template <class K>struct BSTreeNode{BSTreeNode<K>* _left;BSTreeNode<K>* _right;K _key;BSTreeNode(const K& key):_key(key),_left(nullptr),_right(nullptr){}};template <class K>class BSTree{typedef BSTreeNode<K> Node;public:BSTree():_root(nullptr){}BSTree(const BSTree<K>& t){_root = Copy(t._root);}BSTree<K>& operator = (BSTree<K> t){swap(_root, t._root);return *this;}~BSTree(){Destroy(_root);_root = nullptr;}bool Insert(const K& key){if (_root == nullptr){_root = new Node(key);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(key);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}bool find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return true;}}return false;}bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{//左为空if (cur->_left == nullptr){//删除根结点//if(parent==nullptr)if (cur == _root){_root = cur->_right;}else{if (parent->_left == cur){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}delete cur;}//右为空else if (cur->_right == nullptr){if (cur == _root){_root = cur->_left;}else{if (parent->_left == cur){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}delete cur;}//左右都不为空,找替换节点else{//不能初始化为nullptrNode* parent = cur;//右子树最小节点Node* minRight = cur->_right;while (minRight->_left){parent = minRight;minRight = minRight->_left;}cur->_key = minRight->_key;//判断minRight是父亲的左还是右if (minRight == parent->_left){parent->_left = minRight->_right;}else{parent->_right = minRight->_right;}delete minRight;}return true;}}return false;}void InOrder(){_InOrder(_root);cout << endl;}        //递归bool InsertR(const K& key){return _InsertR(_root, key);}bool FindR(const K& key){return _FindR(_root, key);}bool EraseR(const K& key){return _EraseR(_root, key);}private:void Destroy(Node* root){if (root == nullptr){return;}Destroy(root->_left);Destroy(root->_right);delete root;}Node* Copy(Node* root){if (root == nullptr)return nullptr;Node* newRoot = new Node(root->_key);newRoot->_left = Copy(root->_left);newRoot->_right = Copy(root->_right);return newRoot;}bool _EraseR(Node*& root, const K& key){if (root == nullptr){return false;}if (root->_key < key){return _EraseR(root->_right, key);}else if (root->_key > key){return _EraseR(root->_left, key);}else{Node* del = root;if (root->_right == nullptr){root = root->_left;}else if (root->_left == nullptr){root = root->_right;}else{Node* minRight = root->_right;while (minRight->_left){minRight = minRight->_left;}swap(root->_key, minRight->_key);return _EraseR(root->_right, key);}delete del;return true;}}bool _InsertR(Node*& root, const K& key){if (root == nullptr){root = new Node(key);return true;}else if (root->_key < key)return _InsertR(root->_right, key);else if (root->_key > key)return _InsertR(root->_left, key);elsereturn false;}bool _FindR(Node* root, const K& key){if (root == nullptr) return false;else if (root->_key < key) return _FindR(root->_right, key);else if (root->_key > key) return _FindR(root->_left, key);else return true;}void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}Node* _root = nullptr;};}namespace KV{template <class K,class V>struct BSTreeNode{BSTreeNode<K,V>* _left;BSTreeNode<K,V>* _right;K _key;V _value;BSTreeNode(const K& key,const V&value):_key(key),_value(value),_left(nullptr),_right(nullptr){}};template <class K,class V>class BSTree{typedef BSTreeNode<K, V> Node;public:bool Insert(const K& key, const V& value){if (_root == nullptr){_root = new Node(key, value);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(key, value);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}Node* find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return cur;}}return nullptr;}void InOrder(){_InOrder(_root);}private:void _InOrder(Node* root){if (root == nullptr) return;_InOrder(root->_left);cout << root->_key << ":"<<root->_value<<endl;_InOrder(root->_right);}Node* _root = nullptr;};}void TestBSTree1(){int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };K::BSTree<int> t;for (auto e : a){t.Insert(e);}t.InOrder();K::BSTree<int> copyt(t);copyt.InOrder();t.InsertR(9);t.InOrder();t.EraseR(9);t.InOrder();t.EraseR(3);t.InOrder();for (auto e : a){t.EraseR(e);    t.InOrder();}}void TestBSTree2(){KV::BSTree<string, string> dict;dict.Insert("sort", "排序");dict.Insert("string", "字符串");dict.Insert("left", "左");dict.Insert("right", "右");string str;while (cin >> str){KV::BSTreeNode<string, string>* ret = dict.find(str);if (ret){cout << ret->_value << endl;}else{cout << "找不到" << endl;}}}void TestBSTree3(){string arr[] = { "苹果","西瓜","苹果" };KV::BSTree<string, int> countTree;for (auto e : arr){auto* ret = countTree.find(e);if (ret == nullptr){countTree.Insert(e, 1);}else{ret->_value++;}}countTree.InOrder();}

#include "BSTree.h"int main(){    //TestBSTree1();TestBSTree2();    //TestBSTree3();return 0;}

五、题目练习

根据二叉树创建字符串

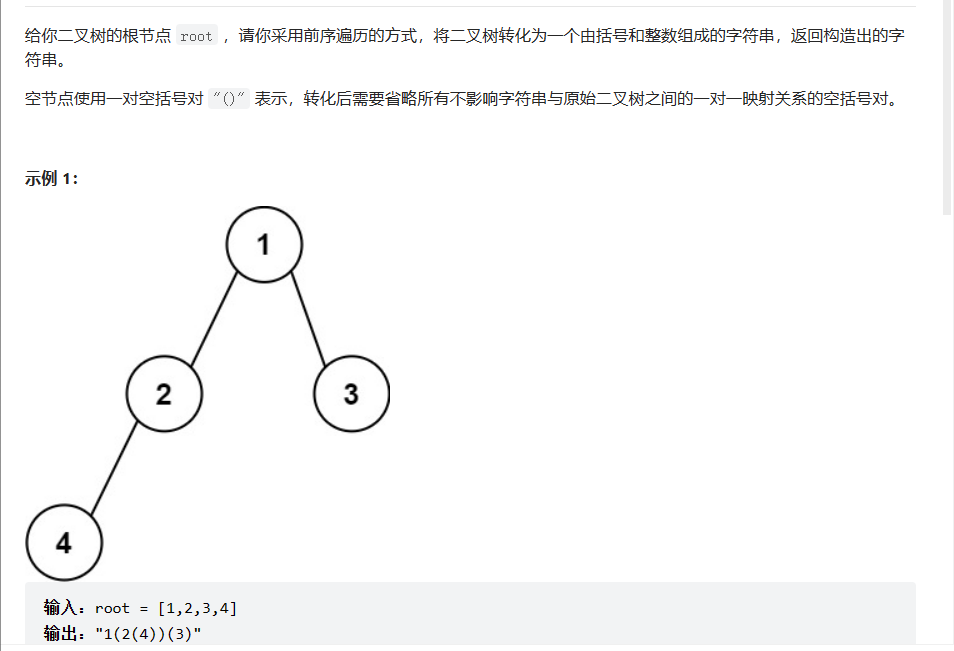
前序遍历，左为空，右不为空的括号不可以省略，右为空的括号可以省略

class Solution {public:    string tree2str(TreeNode* root) {        if(root == nullptr) return string();        string ret;        ret += to_string(root->val);        if(root->left)        {            ret+='(';            ret+= tree2str(root->left);            ret+=')';        }        else if(root->right)        {            ret+="()";        }        if(root->right)        {            ret+='(';            ret+=tree2str(root->right);            ret+=')';        }        return ret;    }};

二叉树的层序遍历

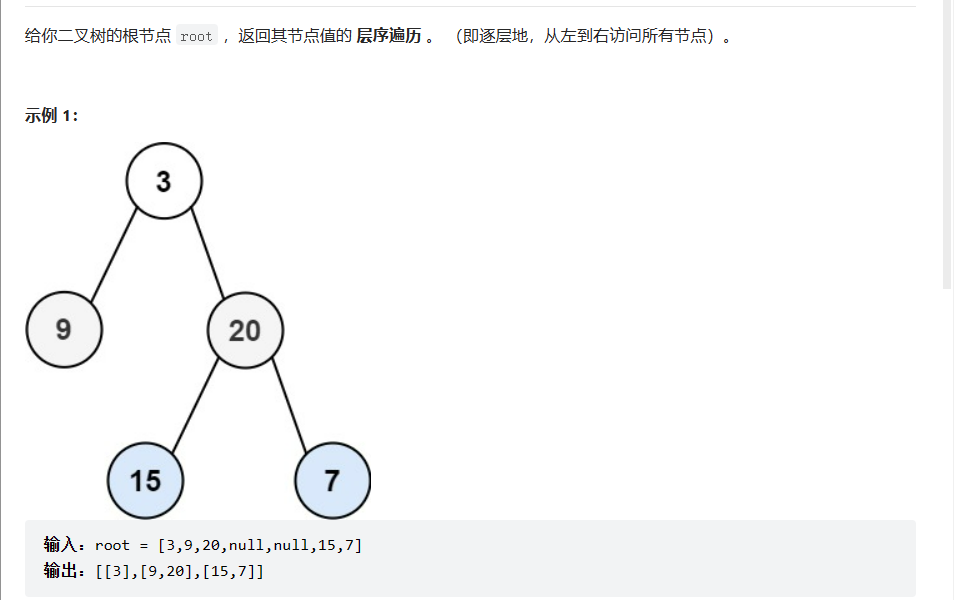
层序遍历，可以通过一个队列来实现，同时定义每次队列的大小

class Solution {public:    vector<vector<int>> levelOrder(TreeNode* root) {        queue<TreeNode*> q;        vector<vector<int>> vv;        size_t levelSize = 0;        if(root)        {            q.push(root);            levelSize=1;        }        while(!q.empty())        {            vector<int> v;            while(levelSize--)            {                TreeNode* front = q.front();                q.pop();                v.push_back(front->val);                if(front->left)                {                    q.push(front->left);                }                if(front->right)                {                    q.push(front->right);                }            }            vv.push_back(v);            levelSize = q.size();        }        return vv;    }};

二叉树的最近公共祖先

class Solution {    bool isInTree(TreeNode*root,TreeNode*x)    {        if(root == nullptr) return false;        if(root == x) return true;        else             return isInTree(root->left,x)                || isInTree(root->right,x);    }public:    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {        if(root==nullptr)            return nullptr;        if(root == p||root==q) return root;        bool pLeft = isInTree(root->left,p);        bool pRight = !pLeft;        bool qLeft = isInTree(root->left,q);        bool qRight = !qLeft;        //一个在左一个在右        if((pLeft&&qRight)||(pRight&&qLeft))            return root;        //同左        if(pLeft&&qLeft)            return lowestCommonAncestor(root->left,p,q);        //同右        else            return lowestCommonAncestor(root->right,p,q);    }};

把根到对应节点的路径存储起来，在找出相交的结点即是最近的公共结点：

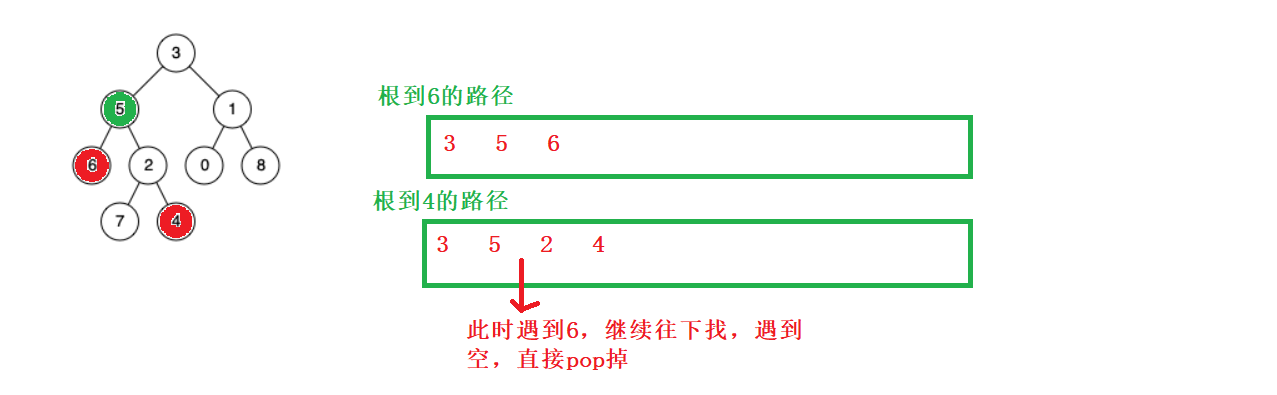
class Solution {    bool GetPath(TreeNode*root,TreeNode*x,stack<TreeNode*>& stack)    {        if(root == nullptr) return false;        stack.push(root);        if(root == x)        {            return true;        }        if(GetPath(root->left,x,stack))            return true;        if(GetPath(root->right,x,stack))            return true;        stack.pop();        return false;    }public:    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {        if(root==nullptr)            return nullptr;        stack<TreeNode*> pPath;        stack<TreeNode*> qPath;        GetPath(root,p,pPath);        GetPath(root,q,qPath);        //长的先pop        while(pPath.size()!=qPath.size())        {            if(pPath.size()>qPath.size())            {                pPath.pop();            }            else                qPath.pop();        }        //同时pop,找出交点        while(pPath.top()!=qPath.top())        {            pPath.pop();            qPath.pop();        }        return pPath.top();    }};

二叉搜索树与双向链表

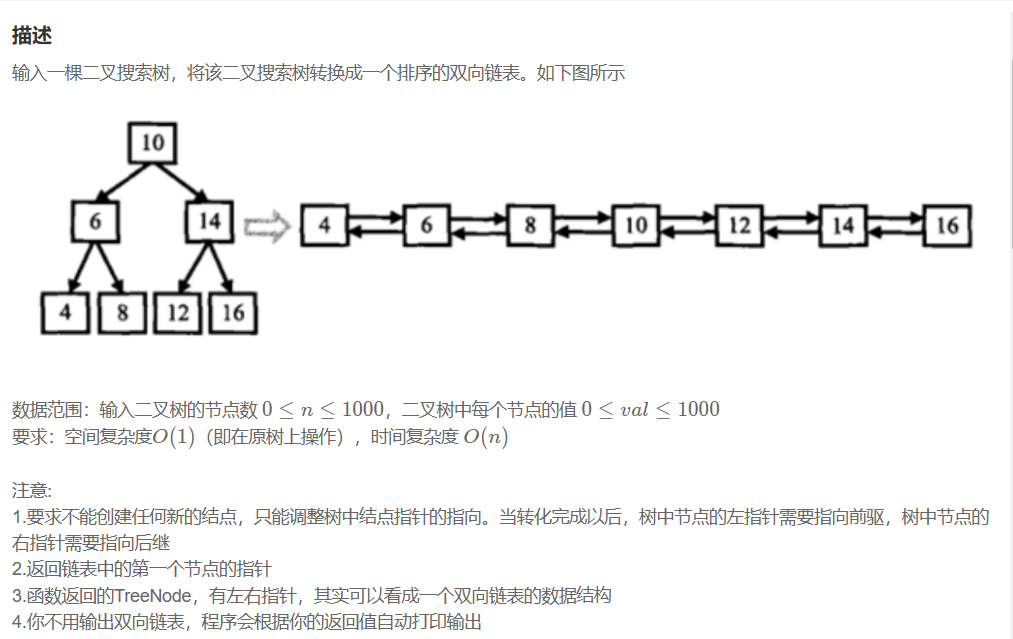
思路一：中序遍历，将节点放到一个vector中，在链接节点，但是空间复杂度不符合题目要求：

class Solution {void InOrder(TreeNode*root,vector<TreeNode*>& v){if(root==nullptr) return;InOrder(root->left,v);v.push_back(root);InOrder(root->right,v);}public:    TreeNode* Convert(TreeNode* pRootOfTree) {if(pRootOfTree==nullptr) return nullptr;vector<TreeNode*> v;InOrder(pRootOfTree,v);if(v.size()<=1) return v[0];v[0]->left =nullptr;v[0]->right = v[1];for(int i =1;i<v.size()-1;i++){v[i]->left = v[i-1];v[i]->right = v[i+1];}v[v.size()-1]->left = v[v.size()-2];v[v.size()-1]->right = nullptr;return v[0];}};

思路二：递归直接进行转换

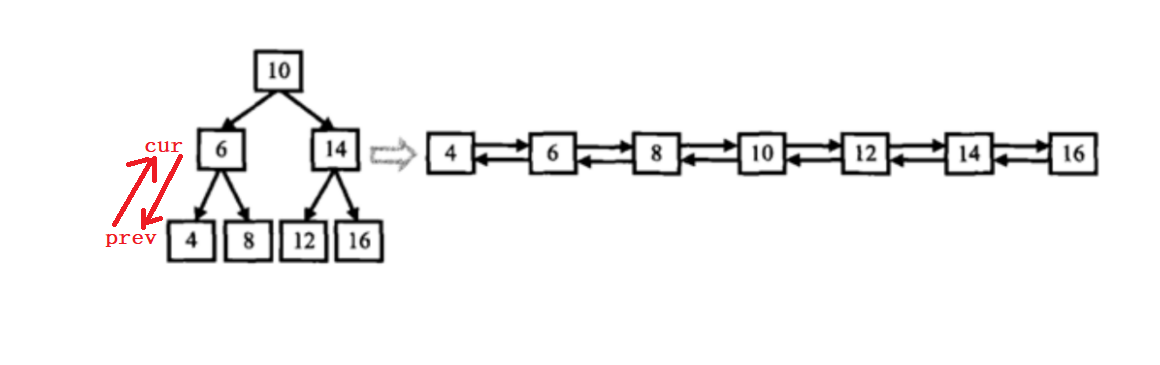
class Solution {void InOrder(TreeNode*cur,TreeNode*&prev){if(cur==nullptr){return;}InOrder(cur->left,prev);cur->left = prev;if(prev){prev->right = cur;}prev = cur;InOrder(cur->right,prev);}public:    TreeNode* Convert(TreeNode* pRootOfTree) {TreeNode*prev = nullptr;InOrder(pRootOfTree,prev);//找头TreeNode*head = pRootOfTree;while(head&&head->left){head = head->left;}return head;}};

从前序与中序遍历序列构造二叉树

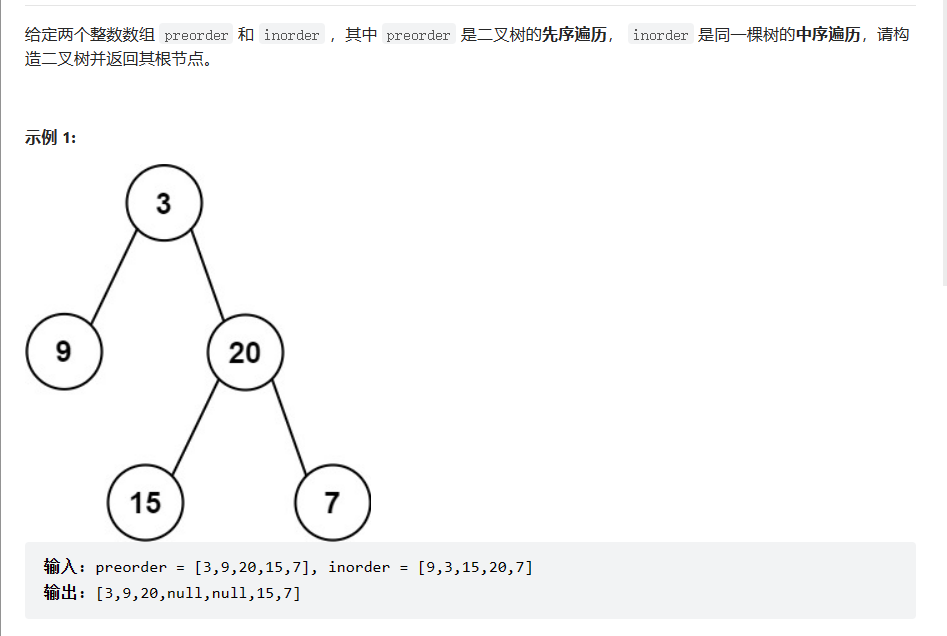
根据前序结果去创建树，前序是根左右，前序第一个元素就是根，在通过中序去进行分割左右子树。子树区间确认是否继续递归创建子树，区间不存在则是空树。所以根据前序先构造根，在通过中序构造左子树、在构造右子树即可。

class Solution {    TreeNode* _buildTree(vector<int>& preorder, vector<int>& inorder,int&prei,int inbegin,int inend)    {        if(inbegin>inend)        {            return nullptr;        }        TreeNode*root = new TreeNode(preorder[prei]);        int rooti = inbegin;        while(inbegin<=inend)        {            if(preorder[prei] == inorder[rooti])            {                break;            }            else rooti++;        }        prei++;        //[inbegin,rooti-1]rooti[rooti+1,inend]        root->left= _buildTree(preorder,inorder,prei,inbegin,rooti-1);        root->right = _buildTree(preorder,inorder,prei,rooti+1,inend);        return root;    }public:    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {        int prei = 0;       return _buildTree(preorder,inorder,prei,0,inorder.size()-1);    }};

传引用问题：因为prei是遍历前序数组开始的下标，整个递归遍历中都要使用，所以我们需要传引用。如果不是传引用而是传值的话，左子树构建好返回，如果此时prei不是传引用，只是形参，无法将上一次递归的结果保留下来，那么也就无构建右子树了。

从中序与后序遍历序列构造二叉树

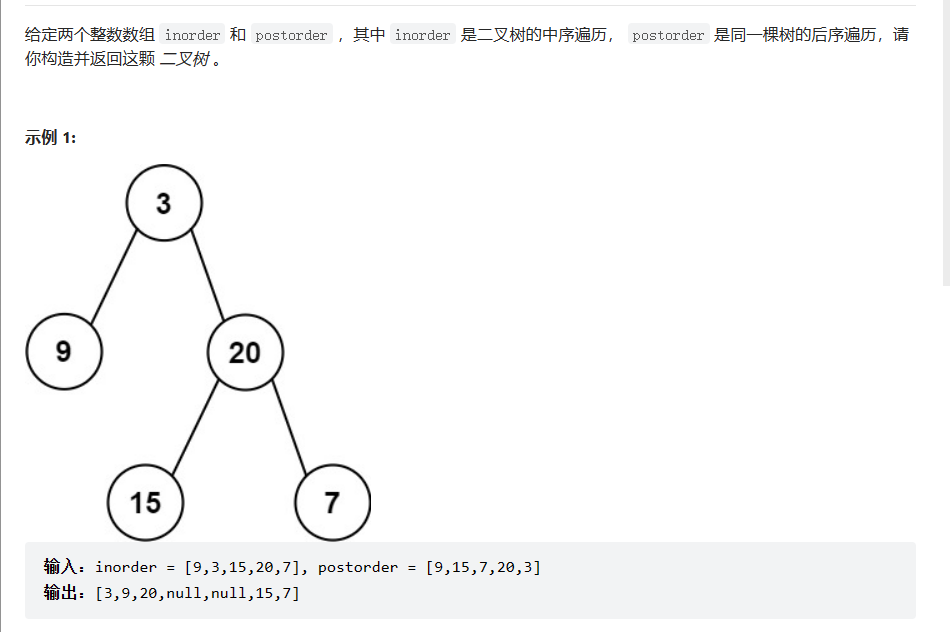
根据后序遍历的最后一个元素可以确定根结点，有了根结点做为切割点然后再去根据中序遍历划分左右区间，在继续下去，构造成二叉树，区间不存在就是空树了。同时，后序遍历是左右根，所以最后一个是根节点。所以当我们构造根结点后，由于前面是右子树，所以先构造右子树，在构造左子数。

class Solution {    TreeNode* _buildTree(vector<int>& inorder, vector<int>& postorder,int &posi,int inbegin,int inend)    {        if(inbegin>inend)        {            return nullptr;        }        TreeNode* root = new TreeNode(postorder[posi]);        int rooti = inbegin;        while(inbegin<=inend)        {            if(postorder[posi] == inorder[rooti])            {                break;            }            else rooti++;        }        posi--;        //[inbegin,rooti-1]rooti[rooti+1,inend];        root->right = _buildTree(inorder,postorder,posi,rooti+1,inend);        root->left = _buildTree(inorder,postorder,posi,inbegin,rooti-1);        return root;    }public:    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {        int posi = postorder.size()-1;        return _buildTree(inorder,postorder,posi,0,inorder.size()-1);    }};

关于“C++二叉搜索树BSTree如何使用”的内容就介绍到这里了，感谢大家的阅读。如果想了解更多行业相关的知识，可以关注编程网其他教程频道，小编每天都会为大家更新不同的知识点。