java数据结构之树的示例分析

这篇文章主要介绍java数据结构之树的示例分析，文中介绍的非常详细，具有一定的参考价值，感兴趣的小伙伴们一定要看完！

树定义和基本术语

定义

树(Tree)是n(n≥0)个结点的有限集T，并且当n＞0时满足下列条件：

（1）有且仅有一个特定的称为根(Root)的结点；

（2）当n＞1时，其余结点可以划分为m(m＞0)个互不相交的有限集T1、T2、…、Tm，每个集Ti(1≤i≤m)均为树，且称为树T的子树(SubTree)。

特别地，不含任何结点(即n＝0)的树，称为空树。

如下就是一棵树的结构：

基本术语

结点：存储数据元素和指向子树的链接，由数据元素和构造数据元素之间关系的引用组成。
孩子结点：树中一个结点的子树的根结点称为这个结点的孩子结点，如图1中的A的孩子结点有B、C、D
双亲结点：树中某个结点有孩子结点(即该结点的度不为0)，该结点称为它孩子结点的双亲结点，也叫前驱结点。双亲结点和孩子结点是相互的，如图1中，A的孩子结点是B、C、D，B、C、D的双亲结点是A。
兄弟结点：具有相同双亲结点(即同一个前驱)的结点称为兄弟结点，如图1中B、B、D为兄弟结点。
结点的度：结点所有子树的个数称为该结点的度，如图1，A的度为3，B的度为2.
树的度：树中所有结点的度的最大值称为树的度，如图1的度为3.
叶子结点：度为0的结点称为叶子结点，也叫终端结点。如图1的K、L、F、G、M、I、J
分支结点：度不为0的结点称为分支结点，也叫非终端结点。如图1的A、B、C、D、E、H
结点的层次：从根结点到树中某结点所经路径的分支数称为该结点的层次。根结点的层次一般为1(也可以自己定义为0)，这样，其它结点的层次是其双亲结点的层次加1.
树的深度：树中所有结点的层次的最大值称为该树的深度(也就是最下面那个结点的层次)。
有序树和无序树：树中任意一个结点的各子树按从左到右是有序的，称为有序树，否则称为无序树。
树的抽象数据类型描述
数据元素：具有相同特性的数据元素的集合。
结构关系：树中数据元素间的结构关系由树的定义确定。

基本操作：树的主要操作有

（1）创建树IntTree(&T)
         创建1个空树T。
（2）销毁树DestroyTree(&T)
（3）构造树CreatTree(&T，deinition)
（4）置空树ClearTree(&T)
          将树T置为空树。
（5）判空树TreeEmpty(T)
（6）求树的深度TreeDepth(T)
（7）获得树根Root(T)
（8）获取结点Value(T，cur_e，&e)
         将树中结点cur_e存入e单元中。
（9）数据赋值Assign(T，cur_e，value)
         将结点value，赋值于树T的结点cur_e中。
（10）获得双亲Parent(T，cur_e)
        返回树T中结点cur_e的双亲结点。
（11）获得最左孩子LeftChild(T，cur_e)
        返回树T中结点cur_e的最左孩子。
（12）获得右兄弟RightSibling(T，cur_e)
        返回树T中结点cur_e的右兄弟。
（13）插入子树InsertChild(&T，&p，i，c)
      将树c插入到树T中p指向结点的第i个子树之前。
（14）删除子树DeleteChild(&T，&p，i)
       删除树T中p指向结点的第i个子树。
（15）遍历树TraverseTree(T，visit())

树的实现

树是一种递归结构，表示方式一般有孩子表示法和孩子兄弟表示法两种。树实现方式有很多种、有可以由广义表的递归实现，也可以有二叉树实现，其中最常见的是将树用孩子兄弟表示法转化成二叉树来实现。

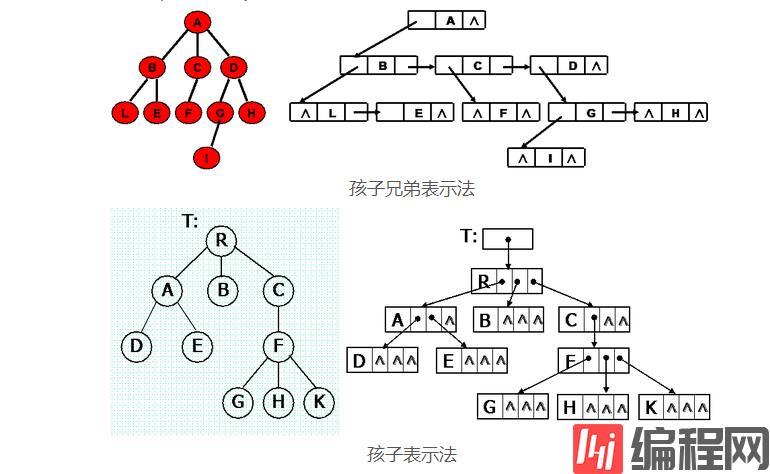
下面以孩子表示法为例讲一下树的实现：

树的定义和实现

package datastructure.tree;import java.util.ArrayList;import java.util.Arrays;import java.util.LinkedList;import java.util.List;public class Tree {private Object data;private List<Tree> childs;public Tree(){data = null;childs = new ArrayList();childs.clear();}public Tree(Object data) {this.data = data;childs = new ArrayList();childs.clear();}public void addnode(Tree tree) {childs.add(tree);}public void clearTree() {data = null;childs.clear();}public int dept() {return dept(this);}private int dept(Tree tree) {if(tree.isEmpty()) {return 0;} else if(tree.isLeaf()) {return 1;} else {int n = childs.size();int[] a = new int[n];for (int i=0; i<n; i++) {if(childs.get(i).isEmpty()) {a[i] = 0+1;} else {a[i] = dept(childs.get(i)) + 1;}}Arrays.sort(a);return a[n-1];}}public Tree getChild(int i) {return childs.get(i);}public Tree getFirstChild() {return childs.get(0);}public Tree getLastChild() {return childs.get(childs.size()-1);}public List<Tree> getChilds() {return childs;}public Object getRootData() {return data;}public Boolean isEmpty() {if(childs.isEmpty() && data == null)         return true;return false;}public Boolean isLeaf() {if(childs.isEmpty())         return true;return false;}public Tree root() {return this;}public void setRootData(Object data) {this.data = data;}public int size() {return size(this);}private int size(Tree tree) {if(tree.isEmpty()) {return 0;} else if(tree.isLeaf()) {return 1;} else {int count = 1;int n = childs.size();for (int i=0; i<n; i++) {if(!childs.get(i).isEmpty()) {count += size(childs.get(i));}}return count;}}}

树的遍历

树的遍历有两种

前根遍历

（1）.访问根结点；

（2）.按照从左到右的次序行根遍历根结点的第一棵子树；

后根遍历

（1）.按照从左到右的次序行根遍历根结点的第一棵子树；

（2）.访问根结点；

Visit.Java

package datastructure.tree;import datastructure.tree.btree.BTree;public interface Visit {public void visit(BTree btree);}

order.java

package datastructure.tree;import java.util.List;public class Order {public void preOrder(Tree root) {if(!root.isEmpty()) {visit(root);for (Tree child : root.getChilds()) {if(child != null) {preOrder(child);}}}}public void postOrder(Tree root) {if(!root.isEmpty()) {for (Tree child : root.getChilds()) {if(child != null) {preOrder(child);}}visit(root);}}public void visit(Tree tree) {System.out.print("\t" + tree.getRootData());}}

测试：

要遍历的树如下：

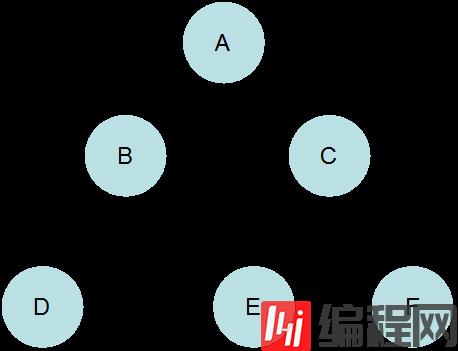
package datastructure.tree;import java.util.Iterator;import java.util.Scanner;public class TreeTest {public static void main(String[] args) {Tree root = new Tree("A");root.addNode(new Tree("B"));root.addNode(new Tree("C"));root.addNode(new Tree("D"));Tree t = null;t = root.getChild(0);t.addNode(new Tree("L"));t.addNode(new Tree("E"));t = root.getChild(1);t.addNode(new Tree("F"));t = root.getChild(2);t.addNode(new Tree("I"));t.addNode(new Tree("H"));t = t.getFirstChild();t.addNode(new Tree("L"));System.out.println("first node:" + root.getRootData());//System.out.println("size:" + root.size()); //System.out.println("dept:" + root.dept()); System.out.println("is left:" + root.isLeaf());System.out.println("data:" + root.getRootData());Order order = new Order();System.out.println("前根遍历：");order.preOrder(root);System.out.println("\n后根遍历：");order.postOrder(root);}}

结果：

first node:A
is left:false
data:A
前根遍历：
A BL E C F DI L H
后根遍历：
B LE C F D IL H A

以上是“java数据结构之树的示例分析”这篇文章的所有内容，感谢各位的阅读！希望分享的内容对大家有帮助，更多相关知识，欢迎关注编程网精选频道！