Python 官方文档:入门教程 => 点击学习
目录一.Morris遍历1.什么是Morris遍历2.基本思想3.Morris遍历的优点和缺点4.二叉树的线索化二.中序Morris遍历1.中序Morris遍历的分析2.中序Morr
Morris遍历是一种用于二叉树遍历的算法,它可以在不使用栈或队列的情况下实现中序遍历。该算法的时间复杂度为O(n),空间复杂度为O(1)。
Morris遍历的基本思想是,利用叶子节点的空指针来存储临时信息,以达到节省空间的目的。具体来说,对于当前遍历到的节点,如果它有左子节点,就找到左子树中最右边的节点,将其右子节点指向当前节点,然后将当前节点更新为其左子节点。如果它没有左子节点,就输出当前节点的值,并将当前节点更新为其右子节点。重复以上步骤,直到遍历完整棵树。
Morris遍历的优点是空间复杂度低O(1),但它的缺点是会改变原来的二叉树结构,因此需要在遍历完后还原二叉树。此外,该算法可能会比递归或使用栈的算法稍微慢一些。
二叉树的线索化,主要是利用了叶子结点中的空指针域,存放了在某种遍历顺序下的前驱或者后续结点,从而达到了线索二叉树的目的
例如,下图中序遍历结果展示如下,根据中序遍历对空指针域进行线索化
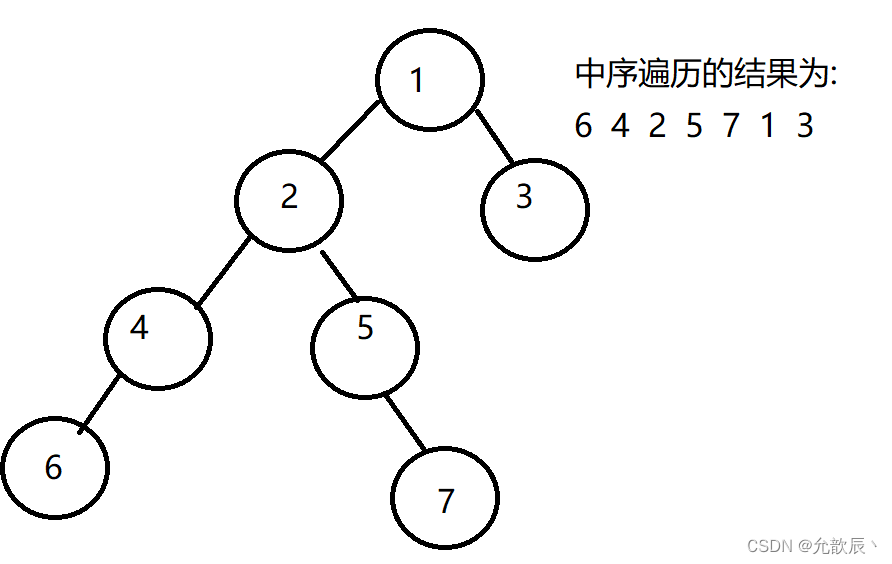
线索化的二叉树为下, 画在左边表示left结点指向,画在右边表示right指向,例如7的前驱结点为5,那么7的left指向5,7的后继节点为1,那么7的right指向1
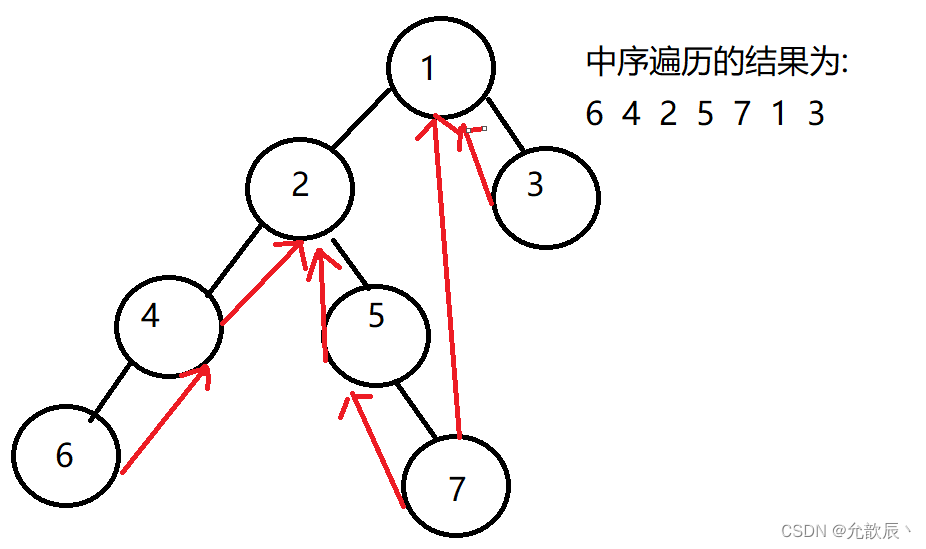
由此,我们可能总结出这样的结论:中序遍历二叉树的指向当前结点的结点为当前结点的左子树的最右端结点,例如指向1的结点为1的左节点2的最右端结点为7,指向2结点的为2的左节点4的最右端结点4.这一点在之后的morris遍历中很重要
具体的代码实现如下:
public class InorderThreadedBinaryTree {
private ThreadTreenode pre = null;
public void threadedNodes(ThreadTreeNode node) {
//如果node==null,不能线索化
if (node == null) {
return;
}
//1、先线索化左子树
threadedNodes(node.left);
//2、线索化当前结点
//处理当前结点的前驱结点
//以8为例来理解
//8结点的.left = null,8结点的.leftType = 1
if (node.left == null) {
//让当前结点的左指针指向前驱结点
node.left = pre;
//修改当前结点的左指针的类型,指向前驱结点
node.leftType = 1;
}
//处理后继结点
if (pre != null && pre.right == null) {
//让当前结点的右指针指向当前结点
pre.right = node;
//修改当前结点的右指针的类型=
pre.rightType = 1;
}
//每处理一个结点后,让当前结点是下一个结点的前驱结点
pre = node;
//3、线索化右子树
threadedNodes(node.right);
}
}
class ThreadTreeNode {
int val;
ThreadTreeNode left;
//0为非线索化,1为线索化
int leftType;
ThreadTreeNode right;
//0为非线索化,1为线索化
int rightType;
public ThreadTreeNode(int val) {
this.val = val;
}
}但是在实现Morris遍历的时候,并不需要把结点的左节点线索化,只需要把结点的右节点进行线索化即可,具体的原因在下面进行分析.
上面我们说了Morris遍历的时候只需要线索化右节点,这里给大家进行解释.当我们在中序遍历一棵树的时候,还比如是这样一棵树,我们一步步的node.left来到了6这个结点,这个结点的left为空,所以我们打印6这个结点的值,此时我们需要返回上一个结点,如果我们是要中序递归进行遍历的话,需要返回上一个栈,而我们Morris遍历的时候无法进行递归的返回,所以这个时候我们只需要把6的right结点进行线索化,这个时候6的right指向4,我们就可以返回到4,把4这个结点进行打印,4也线索化返回了2,把2进行打印,然后进行2的right结点5,5的left结点为空,因此打印5,之后进入到5的right结点7,打印7,7的right结点也进行了线索化,进入7的right结点为1,然后打印1,进入3结点并且打印
因为最好不要改变树的结构,所以我们在打印的时候,将线索化的结点的right结点置为空.
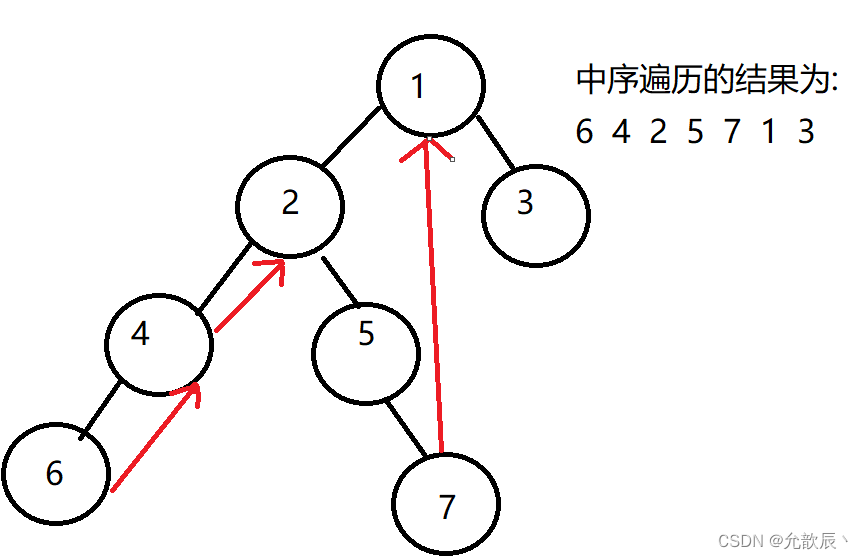
Morris遍历是利用了线索二叉树的思想,在遍历的过程中不适用栈,从而达到了空间复杂度为O(1)
具体的实现如下:
1.初始化当前的结点为根结点
2.若当前的结点的左节点为空,则输出当前结点,然后遍历当前结点的右子树,即'curr=curr.right'
3.若当前结点的左节点不为空,则找到当前结点的前驱节点,即当前结点左节点的最右侧结点,记为'prev'
public class Morris {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
TreeNode curr = root;
while (curr != null) {
if (curr.left == null) { // 左子树为空,则输出当前节点,然后遍历右子树
res.add(curr.val); //如果要求直接打印,直接输出System.out.println(curr.val);
curr = curr.right;
} else {
// 找到当前节点的前驱节点
TreeNode prev = curr.left;
while (prev.right != null && prev.right != curr) {
prev = prev.right;
}
if (prev.right == null) {
// 将前驱节点的右子树连接到当前节点
prev.right = curr;
curr = curr.left;
} else {
// 前驱节点的右子树已经连接到当前节点,断开连接,输出当前节点,然后遍历右子树
prev.right = null;
res.add(curr.val);//如果要求直接打印,直接输出System.out.println(curr.val);
curr = curr.right;
}
}
}
return res;
}
}
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) {
val = x;
}
}测试:

还是这样一颗二叉树,输出如下:
[6, 4, 2, 5, 7, 1, 3]
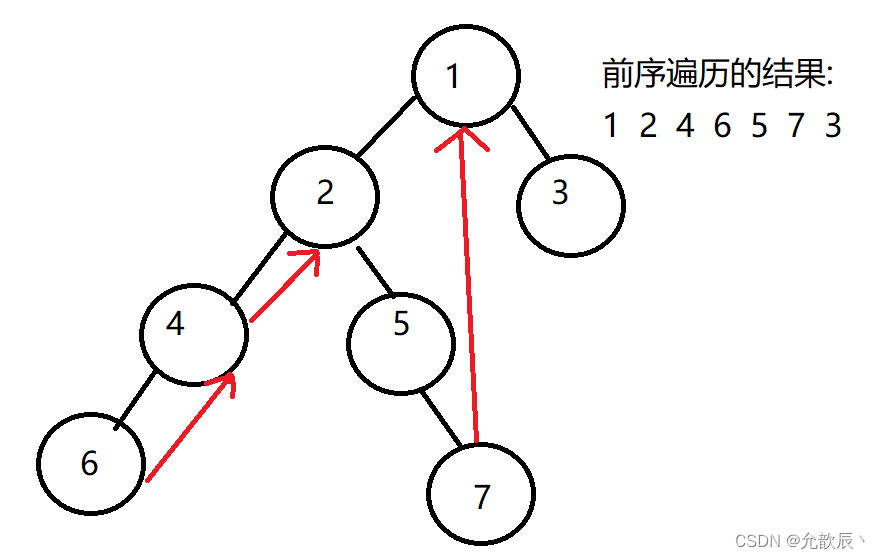
前序和中序的遍历很想,只不过在打印(收集结点信息的时候不同),中序遍历是在当前结点的左节点为空(curr.left==null),或者当前结点已经被线索化(prev.right==curr)的时候进行打印,仔细观察前序遍历的过程,我们通过修改打印的顺序即可.前序遍历是在当前结点的左节点为空(curr.left==null),或者当前结点没有被线索化(prev.right==null)的时候进行打印
具体的思路如下:
1.初始化当前的结点为根结点
2.若当前的结点的左节点为空,则输出当前结点,然后遍历当前结点的右子树,即'curr=curr.right'
3.若当前结点的左节点不为空,则找到当前结点的前驱节点,即当前结点左节点的最右侧结点,记为'prev'
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
TreeNode curr = root;
while (curr != null) {
if (curr.left == null) { // 左子树为空,则输出当前节点,然后遍历右子树
res.add(curr.val);//如果要求直接打印,直接输出System.out.println(curr.val);
curr = curr.right;
} else {
// 找到当前节点的前驱节点
TreeNode prev = curr.left;
while (prev.right != null && prev.right != curr) {
prev = prev.right;
}
if (prev.right == null) {
res.add(curr.val);//如果要求直接打印,直接输出System.out.println(curr.val);
// 将前驱节点的右子树连接到当前节点
prev.right = curr;
curr = curr.left;
} else {
// 前驱节点的右子树已经连接到当前节点,断开连接,输出当前节点,然后遍历右子树
prev.right = null;
curr = curr.right;
}
}
}
return res;
}测试:
public static void main(String[] args) {
TreeNode root = new TreeNode(1);
root.left = new TreeNode(2);
root.left.right = new TreeNode(5);
root.left.right.right = new TreeNode(7);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.left.left.left = new TreeNode(6);
System.out.println(preorderTraversal(root));
}还是这样一颗二叉树,输出如下:
[1, 2, 4, 6, 5, 7, 3]
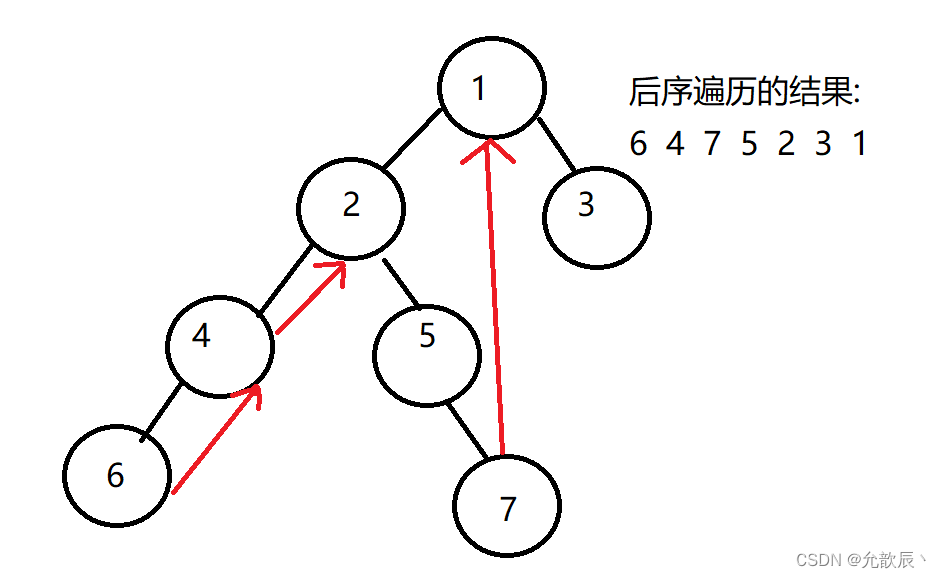
后序Morris遍历实现起来有一定的难度,但是基本代码还是不变,只是在打印的地方有略微的区别,
具体的思路如下:
1.初始化当前的结点为根结点
2.若当前的结点的左节点为空,则输出当前结点,然后遍历当前结点的右子树,即'curr=curr.right'
3.若当前结点的左节点不为空,则找到当前结点的前驱节点,即当前结点左节点的最右侧结点,记为'prev'
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
TreeNode dump = new TreeNode(0);//建立一个临时结点
dump.left = root; //设置dump的左节点为root
TreeNode curr = dump; //当前节点为dump
while (curr != null) {
if (curr.left == null) { // 左子树为空,则输出当前节点,然后遍历右子树
curr = curr.right;
} else {
// 找到当前节点的前驱节点
TreeNode prev = curr.left;
while (prev.right != null && prev.right != curr) {
prev = prev.right;
}
if (prev.right == null) {
// 将前驱节点的右子树连接到当前节点
prev.right = curr;
curr = curr.left;
} else {
reverseAddNodes(curr.left, prev, res);
// 前驱节点的右子树已经连接到当前节点,断开连接,输出当前节点,然后遍历右子树
prev.right = null;
curr = curr.right;
}
}
}
return res;
}
private void reverseAddNodes(TreeNode begin, TreeNode end, List<Integer> res) {
reverseNodes(begin, end); //将begin到end的进行逆序连接
TreeNode curr = end;
while (true) {//将逆序连接后端begin到end添加
res.add(curr.val);
if (curr == begin)
break;
curr = curr.right;
}
reverseNodes(end, begin);//恢复之前的连接状态
}
private void reverseNodes(TreeNode begin, TreeNode end) {
TreeNode prev = begin;
TreeNode curr = prev.right;
TreeNode post;
while (prev != end) {
post = curr.right;
curr.right = prev;
prev = curr;
curr = post;
}
}测试:
public static void main(String[] args) {
TreeNode root = new TreeNode(1);
root.left = new TreeNode(2);
root.left.right = new TreeNode(5);
root.left.right.right = new TreeNode(7);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.left.left.left = new TreeNode(6);
System.out.println(postorderTraversal(root));
}还是这样一颗二叉树,输出如下:
[6, 4, 7, 5, 2, 3, 1]
到此这篇关于Java Morris遍历算法及其在二叉树中的应用的文章就介绍到这了,更多相关Java Morris遍历算法内容请搜索编程网以前的文章或继续浏览下面的相关文章希望大家以后多多支持编程网!
--结束END--
本文标题: JavaMorris遍历算法及其在二叉树中的应用
本文链接: https://lsjlt.com/news/211836.html(转载时请注明来源链接)
有问题或投稿请发送至: 邮箱/279061341@qq.com QQ/279061341
2024-03-01
2024-03-01
2024-03-01
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
回答
回答
回答
回答
回答
回答
回答
回答
回答
回答
0