扫码关注官方微信

扫码下载APP
返回顶部
首页 > 资讯 > 后端开发 > Python >使用python实现kmean算法
  • 356

0
分享到

使用python实现kmean算法

python算法python实现kmean 2023-05-17 11:05:00 356人浏览 泡泡鱼

Python 官方文档：入门教程 => 点击学习

摘要

目录1. 简介2. kmean算法过程2.1 簇个数的选择2.2 聚类评价指标2.2.1 轮廓系数2.2.2 紧密性指标2.2.3 间隔性指标3. 代码4. 输出结果4.1 命令行输

1. 简介

kmean 是无监督学习的一种算法，主要是用来进行聚类分析的，他会在数据集中算出几个点作为簇中心，求这些数据集与这些簇中心的距离，并将距离同一个簇中心距离最近的数据归为一类。因此，kmean最重要的地方便是关于簇中心的选择。

他的算法流程简单总结如下

  • 簇个数的选择；
  • 计算样本到选取的簇中心距离，划分样本，将距离同一个簇中心最近的样本归为一类；
  • 设置一个迭代次数，不断更新簇中心；

2. kmean算法过程

kmean算法过程

这里初始簇中心的选择并不是随机选择因为随机选择的话，有的簇中心可能会重叠，这里改为了先选择距离最远的两个样本作为两个初始簇中心，下一个簇中心就从距离之前的簇中心距离最近的样本中将距离最远的作为下一个，如此反复直到满足定义的k大小。同时图中的新的簇中心的更新应该是新老簇中心不相等时才更新才对。其实kmean的效果好坏很大的程度上取决于簇中心数量和初始簇中心的选择上，并且他适合一些聚集成簇的样本进行划分。

2.1 簇个数的选择

  • 画图法： 最直接的办法还是画图，从图中直接看整个样本大概分为几大类，这种办法适合低维（1-3维）的数据，对于高维数据很难直接成图，不过可以通过特征提取选择能体现样本差异的特征维（这里的差异很难定义，毕竟是无监督学习，可以简单认为成图后样本聚集为几类，这些类间间隔较远），或者直接降维为低维度数据成图观察。
  • 穷举k法： 通过定义一系列不同的簇个数，并通过聚类指标评价这些不同簇个数的效果，选择效果最好的那个；

2.2 聚类评价指标

还有更多的评价指标，这里我选择了一些简单的，易于实现的。

2.2.1 轮廓系数

参考：https://baike.baidu.com/item/%E8%BD%AE%E5%BB%93%E7%B3%BB%E6%95%B0/17361607?fr=aladdin

轮廓系数

补充：如果Si接近0代表该样本越可能在类的边界上；越接近-1代表越可能属于其他类；

2.2.2 紧密性指标

紧密性指标

这里指的是先计算同簇的样本距离簇中心的平均距离CPi，再计算CPi的平均值；

2.2.3 间隔性指标

间隔性指标

3. 代码

数据集：经典的鸢尾花数据集，里面收录了三个不同品种共四个不同性状的数据。

#数据集
5.1,3.5,1.4,0.2,Iris-setosa
4.9,3.0,1.4,0.2,Iris-setosa
4.7,3.2,1.3,0.2,Iris-setosa
4.6,3.1,1.5,0.2,Iris-setosa
5.0,3.6,1.4,0.2,Iris-setosa
5.4,3.9,1.7,0.4,Iris-setosa
4.6,3.4,1.4,0.3,Iris-setosa
5.0,3.4,1.5,0.2,Iris-setosa
4.4,2.9,1.4,0.2,Iris-setosa
4.9,3.1,1.5,0.1,Iris-setosa
5.4,3.7,1.5,0.2,Iris-setosa
4.8,3.4,1.6,0.2,Iris-setosa
4.8,3.0,1.4,0.1,Iris-setosa
4.3,3.0,1.1,0.1,Iris-setosa
5.8,4.0,1.2,0.2,Iris-setosa
5.7,4.4,1.5,0.4,Iris-setosa
5.4,3.9,1.3,0.4,Iris-setosa
5.1,3.5,1.4,0.3,Iris-setosa
5.7,3.8,1.7,0.3,Iris-setosa
5.1,3.8,1.5,0.3,Iris-setosa
5.4,3.4,1.7,0.2,Iris-setosa
5.1,3.7,1.5,0.4,Iris-setosa
4.6,3.6,1.0,0.2,Iris-setosa
5.1,3.3,1.7,0.5,Iris-setosa
4.8,3.4,1.9,0.2,Iris-setosa
5.0,3.0,1.6,0.2,Iris-setosa
5.0,3.4,1.6,0.4,Iris-setosa
5.2,3.5,1.5,0.2,Iris-setosa
5.2,3.4,1.4,0.2,Iris-setosa
4.7,3.2,1.6,0.2,Iris-setosa
4.8,3.1,1.6,0.2,Iris-setosa
5.4,3.4,1.5,0.4,Iris-setosa
5.2,4.1,1.5,0.1,Iris-setosa
5.5,4.2,1.4,0.2,Iris-setosa
4.9,3.1,1.5,0.1,Iris-setosa
5.0,3.2,1.2,0.2,Iris-setosa
5.5,3.5,1.3,0.2,Iris-setosa
4.9,3.1,1.5,0.1,Iris-setosa
4.4,3.0,1.3,0.2,Iris-setosa
5.1,3.4,1.5,0.2,Iris-setosa
5.0,3.5,1.3,0.3,Iris-setosa
4.5,2.3,1.3,0.3,Iris-setosa
4.4,3.2,1.3,0.2,Iris-setosa
5.0,3.5,1.6,0.6,Iris-setosa
5.1,3.8,1.9,0.4,Iris-setosa
4.8,3.0,1.4,0.3,Iris-setosa
5.1,3.8,1.6,0.2,Iris-setosa
4.6,3.2,1.4,0.2,Iris-setosa
5.3,3.7,1.5,0.2,Iris-setosa
5.0,3.3,1.4,0.2,Iris-setosa
7.0,3.2,4.7,1.4,Iris-versicolor
6.4,3.2,4.5,1.5,Iris-versicolor
6.9,3.1,4.9,1.5,Iris-versicolor
5.5,2.3,4.0,1.3,Iris-versicolor
6.5,2.8,4.6,1.5,Iris-versicolor
5.7,2.8,4.5,1.3,Iris-versicolor
6.3,3.3,4.7,1.6,Iris-versicolor
4.9,2.4,3.3,1.0,Iris-versicolor
6.6,2.9,4.6,1.3,Iris-versicolor
5.2,2.7,3.9,1.4,Iris-versicolor
5.0,2.0,3.5,1.0,Iris-versicolor
5.9,3.0,4.2,1.5,Iris-versicolor
6.0,2.2,4.0,1.0,Iris-versicolor
6.1,2.9,4.7,1.4,Iris-versicolor
5.6,2.9,3.6,1.3,Iris-versicolor
6.7,3.1,4.4,1.4,Iris-versicolor
5.6,3.0,4.5,1.5,Iris-versicolor
5.8,2.7,4.1,1.0,Iris-versicolor
6.2,2.2,4.5,1.5,Iris-versicolor
5.6,2.5,3.9,1.1,Iris-versicolor
5.9,3.2,4.8,1.8,Iris-versicolor
6.1,2.8,4.0,1.3,Iris-versicolor
6.3,2.5,4.9,1.5,Iris-versicolor
6.1,2.8,4.7,1.2,Iris-versicolor
6.4,2.9,4.3,1.3,Iris-versicolor
6.6,3.0,4.4,1.4,Iris-versicolor
6.8,2.8,4.8,1.4,Iris-versicolor
6.7,3.0,5.0,1.7,Iris-versicolor
6.0,2.9,4.5,1.5,Iris-versicolor
5.7,2.6,3.5,1.0,Iris-versicolor
5.5,2.4,3.8,1.1,Iris-versicolor
5.5,2.4,3.7,1.0,Iris-versicolor
5.8,2.7,3.9,1.2,Iris-versicolor
6.0,2.7,5.1,1.6,Iris-versicolor
5.4,3.0,4.5,1.5,Iris-versicolor
6.0,3.4,4.5,1.6,Iris-versicolor
6.7,3.1,4.7,1.5,Iris-versicolor
6.3,2.3,4.4,1.3,Iris-versicolor
5.6,3.0,4.1,1.3,Iris-versicolor
5.5,2.5,4.0,1.3,Iris-versicolor
5.5,2.6,4.4,1.2,Iris-versicolor
6.1,3.0,4.6,1.4,Iris-versicolor
5.8,2.6,4.0,1.2,Iris-versicolor
5.0,2.3,3.3,1.0,Iris-versicolor
5.6,2.7,4.2,1.3,Iris-versicolor
5.7,3.0,4.2,1.2,Iris-versicolor
5.7,2.9,4.2,1.3,Iris-versicolor
6.2,2.9,4.3,1.3,Iris-versicolor
5.1,2.5,3.0,1.1,Iris-versicolor
5.7,2.8,4.1,1.3,Iris-versicolor
6.3,3.3,6.0,2.5,Iris-virginica
5.8,2.7,5.1,1.9,Iris-virginica
7.1,3.0,5.9,2.1,Iris-virginica
6.3,2.9,5.6,1.8,Iris-virginica
6.5,3.0,5.8,2.2,Iris-virginica
7.6,3.0,6.6,2.1,Iris-virginica
4.9,2.5,4.5,1.7,Iris-virginica
7.3,2.9,6.3,1.8,Iris-virginica
6.7,2.5,5.8,1.8,Iris-virginica
7.2,3.6,6.1,2.5,Iris-virginica
6.5,3.2,5.1,2.0,Iris-virginica
6.4,2.7,5.3,1.9,Iris-virginica
6.8,3.0,5.5,2.1,Iris-virginica
5.7,2.5,5.0,2.0,Iris-virginica
5.8,2.8,5.1,2.4,Iris-virginica
6.4,3.2,5.3,2.3,Iris-virginica
6.5,3.0,5.5,1.8,Iris-virginica
7.7,3.8,6.7,2.2,Iris-virginica
7.7,2.6,6.9,2.3,Iris-virginica
6.0,2.2,5.0,1.5,Iris-virginica
6.9,3.2,5.7,2.3,Iris-virginica
5.6,2.8,4.9,2.0,Iris-virginica
7.7,2.8,6.7,2.0,Iris-virginica
6.3,2.7,4.9,1.8,Iris-virginica
6.7,3.3,5.7,2.1,Iris-virginica
7.2,3.2,6.0,1.8,Iris-virginica
6.2,2.8,4.8,1.8,Iris-virginica
6.1,3.0,4.9,1.8,Iris-virginica
6.4,2.8,5.6,2.1,Iris-virginica
7.2,3.0,5.8,1.6,Iris-virginica
7.4,2.8,6.1,1.9,Iris-virginica
7.9,3.8,6.4,2.0,Iris-virginica
6.4,2.8,5.6,2.2,Iris-virginica
6.3,2.8,5.1,1.5,Iris-virginica
6.1,2.6,5.6,1.4,Iris-virginica
7.7,3.0,6.1,2.3,Iris-virginica
6.3,3.4,5.6,2.4,Iris-virginica
6.4,3.1,5.5,1.8,Iris-virginica
6.0,3.0,4.8,1.8,Iris-virginica
6.9,3.1,5.4,2.1,Iris-virginica
6.7,3.1,5.6,2.4,Iris-virginica
6.9,3.1,5.1,2.3,Iris-virginica
5.8,2.7,5.1,1.9,Iris-virginica
6.8,3.2,5.9,2.3,Iris-virginica
6.7,3.3,5.7,2.5,Iris-virginica
6.7,3.0,5.2,2.3,Iris-virginica
6.3,2.5,5.0,1.9,Iris-virginica
6.5,3.0,5.2,2.0,Iris-virginica
6.2,3.4,5.4,2.3,Iris-virginica
5.9,3.0,5.1,1.8,Iris-virginica
#python3

#----------------------------
# author: little shark
# date: 2022/3/12
"""
Kmean 实现
"""

from matplotlib import pyplot as plt
import numpy as np
import pandas as pd
import random

class AlGo:
	def __init__(self):
		self.x = None
		self.y = None
		self.rows,self.cols = None, None
		self.dis = None
		self.dis_i = None
		self.rbf_i = None
		self.G_i = None
		self.GDis_i = True
		
	def loadData(self,file):
		"""
		Read file
		"""
		df=pd.read_csv(file,delimiter=",",header=None)
		self.x=df.iloc[:,0:-1].values
		self.y=df.iloc[:,-1].values
		
		self.rows,self.cols=self.x.shape
		#print(self.x.shape)
		
	def dataNORM(self):
		"""
		归一化数据
		"""
		assert self.rows != None or self.cols !=None, "First you must loadData!!!"
		
		#get min matrix
		min_=self.x.min(axis=0).reshape(1,self.cols)
		
		#get max matrix
		max_=self.x.max(axis=0).reshape(1,self.cols)
		
		#get range matrix
		range_=max_-min_

		#update self.x
		self.x=(self.x-min_)/range_
	
	def euDistances(self,x):
		"""
		Get EuclideanDistances matrix
		"""
		assert self.rows != None or self.cols !=None, "First you must loadData!!!"
		
		#输入矩阵大小
		rows,cols = x.shape
		
		#define a empty matrix
		dis=np.zeros(rows**2).reshape(rows,rows)
		
		#fill dis matrix by calculating distance of each point
		for i in range(rows):
			for j in range(rows):
				if i == j:
					dis[i][j] = 0
					continue
				d=sum(pow(x[i]-x[j],2))**0.5
				dis[i][j]=d
				dis[j][i]=d
		
		#get EuclideanDistances matrix
		self.dis=dis.copy()
		self.dis_i=True
		
		return dis
		
		
	def kmean(self,k=3,maxIteration=100,x=None,print_=False):
		"""
		kmean实体
		"""
		assert self.rows != None or self.cols !=None, "First you must loadData!!!"
		assert x.any() != None, "you must import a data to kmean"
		
		#输入矩阵大小
		rows,cols = x.shape
		
		#定义一个标签列表，代表所有样本的类别
		label=np.zeros(rows)
		labelCode=[i for i in range(k)]
		
		#计算输入矩阵的距离矩阵
		dis=self.euDistances(x)
		
		#------------------------------------------
		#选择初始簇中心，数量=k
		#最远的两个点当作簇中心
		max_=0
		maxI=0
		maxJ=0
		for i in range(rows):
			for j in range(rows):
				if dis[i][j] > max_:
					max_ = dis[i][j]
					maxI = i
					maxJ = j
		k1I = maxI
		k2I = maxJ
		k1=x[k1I].reshape(1,cols)
		k2=x[k2I].reshape(1,cols)
		
		Ci=[k1I,k2I] #保存簇中心索引
		C=[k1,k2] #保存簇中心值
		
		#step 3,检索其他簇中心
		for i in range(2,k):
			tempI=[]
			temp=[]
			for j in range(len(C)):
				
				#step 3.1 距离簇中心最近的点
				minI=0
				min_=99999
				index=0
				for d in dis[Ci[j]]:
					#略过本身和已经检索过的点
					if d==0 or index in Ci:
						index+=1
						continue
					if d<min_:
						minI=index
						min_=d
					index+=1
				
				
				#step 3.2 添加距离大小及其索引
				temp.append(dis[Ci[j]][minI])
				tempI.append(minI)
				
			#step 3.3 选择距离已选出的簇中心距离最近的点距离最大的作为下一个簇中心
			nextKI=tempI[temp.index(max(temp))]
			nextK=x[nextKI].reshape(1,cols)
			Ci.append(nextKI)
			C.append(nextK)
		
		#------------------------------------
		#更新label
		for i in range(rows):
			sample=x[i].reshape(1,cols)
			
			#判断距离最近的簇中心
			minI=0
			min_=99999
			for j in range(k):
				disV=self.getDistance(sample,C[j])
				#print(dis)
				if disV<min_:
					minI=j
					min_=disV
			label[i]=labelCode[minI]
		
		#------------------------------------
		#更新簇中心
		for iter in range(maxIteration):
			for j in range(k):
				#获取同类别下的数据
				dataSet=x[label == labelCode[j]]
				if len(dataSet) == 0:
					continue
				
				#计算平均值
				mean_=dataSet.mean(axis=0).reshape(1,cols)
				
				#更新簇中心
				C[j]=mean_
				
			#------------------------------------
			#更新label
			for i in range(rows):
				sample=x[i].reshape(1,cols)
				
				#判断距离最近的簇中心
				minI=0
				min_=99999
				for j in range(k):
					disV=self.getDistance(sample,C[j])
					#print(dis)
					if disV<min_:
						minI=j
						min_=disV
				label[i]=labelCode[minI]
			
			cp = self.CP(label,C,x)
			sp = self.SP(C)
			conCoe = self.contourCoefficient(label,C,x)
			
			if print_:
				print("Iteration %-4d CP = %-7.4f CP = %-7.4f coef = %-7.4f"%(iter,cp,sp,conCoe))
			
		return label,C
	
	def getDistance(self,x1,x2):
		"""
		计算两个向量的几何距离
		"""
		return pow(((x1-x2)**2).sum(),0.5)
				
	def CP(self,label,c,x):
		"""
		紧密性评价指标
		"""
		k = len(c)
		labelCode = np.unique(label)
		
		cp = 0
		for i in range(k):
			#同簇矩阵
			x1 = x[label == i]
			
			if len(x1) == 0:continue
			
			#大小
			rows, cols = x1.shape
			
			#距离簇中心的欧式距离和
			sum_ = pow(((x1 - c[i])**2).sum(),0.5)
			
			cp += sum_/rows
		
		return cp/k
		
	def SP(self,c):
		"""
		间隔性评价指标
		"""
		k = len(c)
		
		sp = 0
		for i in range(k):
			for j in range(1,k):
				sp += self.getDistance(c[i],c[j])
		
		return 2*sp/(k**2-k)
		
	
	def calAi(self,v,vs):
		"""
		轮廓系数中计算ai
		v: 某向量
		vs: 该向量的同簇向量
		"""
		rows,cols = vs.shape
		ai = pow((vs - v)**2,0.5).sum()/rows
		
		return ai
		
	def calBi(self,v,vs,vsLabel):
		"""
		轮廓系数中计算bi
		v: 某向量
		vs: 该向量的非同簇向量
		vscode: 该向量的非同簇向量的label
		"""
		ks = np.unique(vsLabel)
		k = len(ks)
		min_ = 99999
		
		for i in range(k):
			#非同簇中同簇向量
			x1 = vs[vsLabel == i]
			
			if len(x1) == 0:continue
			
			#非同簇中同簇平均距离
			disAver = self.calAi(v,x1)
			
			if disAver < min_:
				min_ = disAver
		
		return min_
		
	def contourCoefficient(self,label,c,x):
		"""
		轮廓系数
		"""
		k = len(c)
		rows,cols = x.shape
		S = np.zeros(rows)
		
		for i in range(rows):
			#同簇样本
			x1 = x[label == label[i]]
			
			#非同簇样本
			x2 = x[label != label[i]]
			label2 = label[label != label[i]]
			
			#当前样本
			sample = x[i]
			
			#ai ,bi 计算
			ai = self.calAi(sample,x1)
			bi = self.calBi(sample,x2,label2)
			
			s = (bi-ai)/max([ai,bi])
			
			S[i] = s
		
		return S.mean()
		
if __name__ == "__main__":
	#-------------------------
	#直接定义簇个数
	a=Algo()
	
	#加载数据
	a.loadData("数据集/iris (2).data")
	
	#运行算法
	label,c = a.kmean(x=a.x,k=3)
	kCode = np.unique(label)
	
	print(label)
	
	#画出数据划分类
	for k in kCode:
		plt.scatter(a.x[label == k][:,0],a.x[label == k][:,2],alpha=0.6,label="sample %d"%k)
	
	#画出簇中心
	for i in range(len(c)):
		plt.scatter(x=c[i][:,0],y=c[i][:,2],color="red",marker="*",label="center %d"%i)
	plt.legend()
	plt.show()
	
	
	#----------------------------
	#穷举k法
	#exit()
	coef = []
	CP = []
	SP = []
	for k in range(2,10):
		label,c = a.kmean(x=a.x,k=k)
		coef.append(a.contourCoefficient(label,c,a.x))
		CP.append(a.SP(c))
		SP.append(a.CP(label,c,a.x))
		print("* When k = %d done *"%k)
	
	plt.subplot(131)
	plt.plot(range(2,10),SP,alpha=0.8,linestyle="--",color="red",label="SP")
	plt.xlabel("K")
	plt.legend()
	
	plt.subplot(132)
	plt.plot(range(2,10),coef,alpha=0.8,linestyle=":",color="green",label="coef")
	plt.xlabel("K")
	plt.legend()
	
	plt.subplot(133)
	plt.plot(range(2,10),CP,alpha=0.8,linestyle="-",color="blue",label="CP")
	plt.xlabel("K")
	plt.legend()
	plt.show()

4. 输出结果

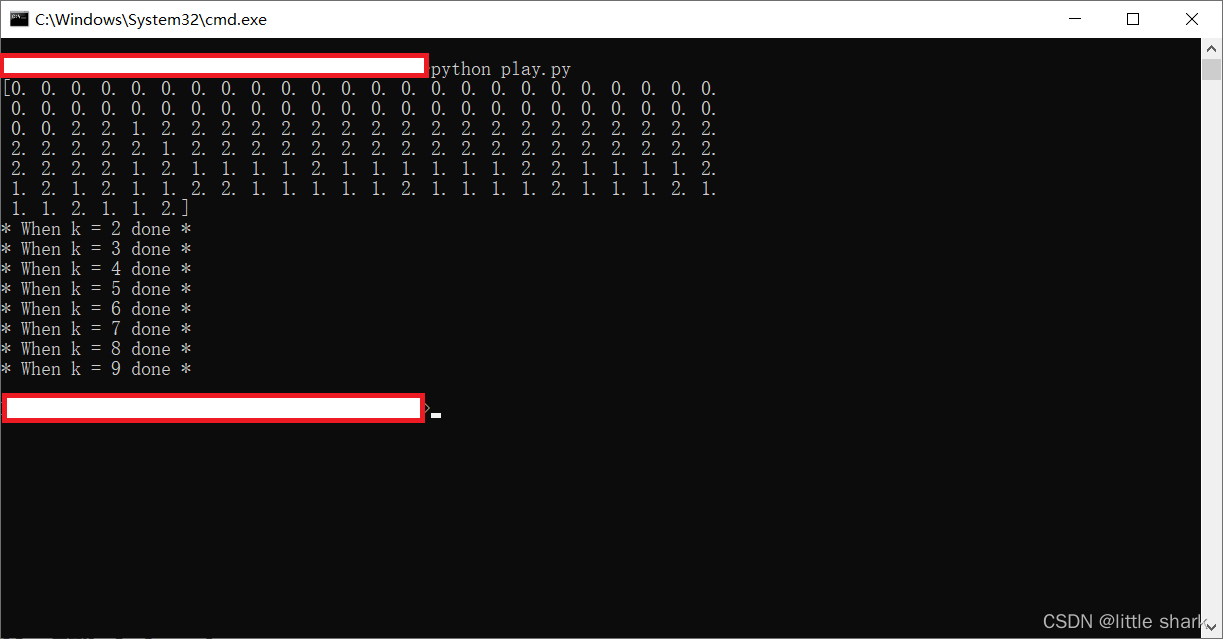
4.1 命令行输出

命令行输出

解释：首先输出的是所有样本的聚类划分，这里并没有打乱样本的顺序进行分析，所以同品种的样本是连续的一大块，大致来看直接定义k=3的划分效果还不错。后面的输出是穷举k法，并计算对应的评价指标进程。

4.2 可视化

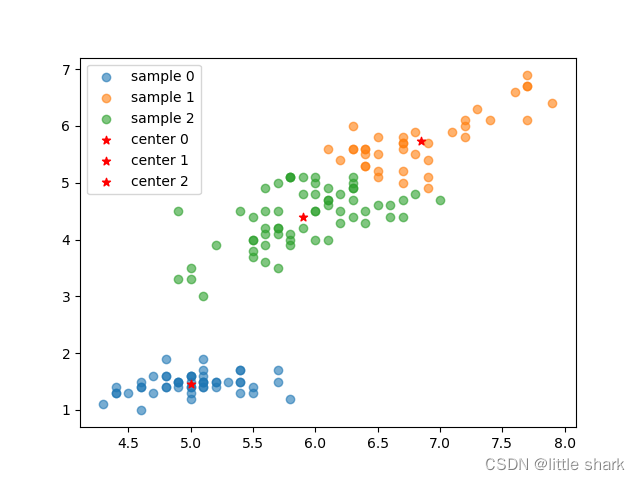
在这里插入图片描述

解释：不同颜色代表不同类别的数据，红色星星代表簇中心，这里数据的维度展示的是第1列和第3列维度。

4.3 穷举k法指标

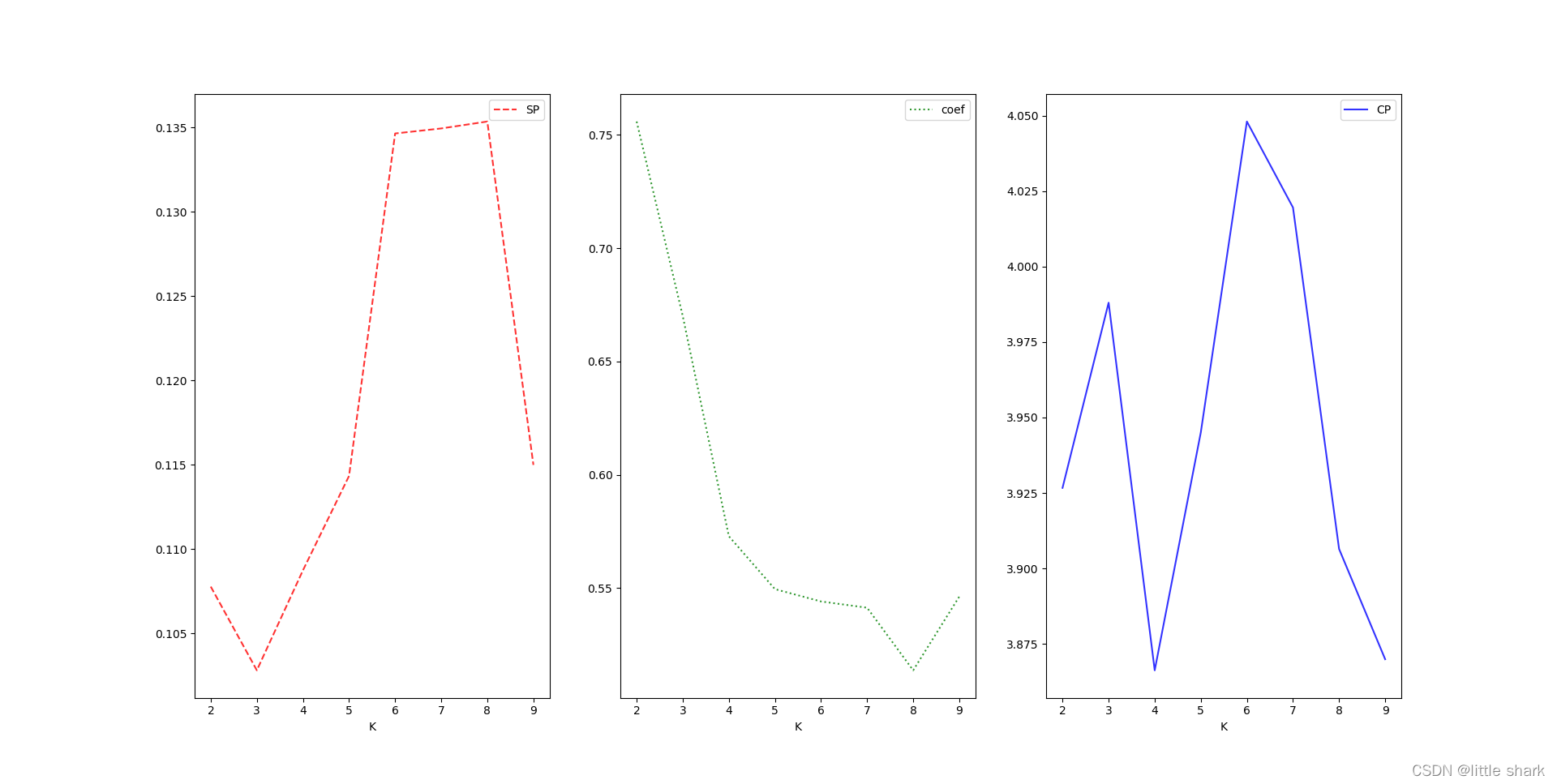
在这里插入图片描述

解释：第一个图是间隔性指标SP用来衡量聚类中心两两之间的平均距离，随着k值增加，有比较明显的波动，可以看见当k=3时有一个最小值，表明k=3时类间的聚类最近，理想情况下我们希望这个这个指标比较大，表明类别区分明显；第二个是轮廓系数，随着k值增加逐渐下降；第三个是紧密性指标，用来衡量内中数据距离簇中心距离，随着k值增加呈现一点的波动；从图中来看任意一个指标都不能准确的表明k=3(真实的簇数)是一个好的簇数量，也许这些指标并不适合用来寻找定义的簇数量。

单从轮廓系数来看，在知道k=3的情况下，越接近1代表聚类越合理，显然是不现实的，且从公式上来说当k=1时，轮廓系数会非常接近1，难道说“大家都是一家人，四海皆兄弟”吗？不太可能吧，且k=2的时候系数为0.75，难道划分为2更好吗？显然在知道真实分类情况下也不适合，那么我们统计分析的结果真的就和真实一样吗？

首先从kmean上来说，他是无监督的算法，这些数据是没有先验的标签的，他是用来衡量数据相似情况，并把相似度较高的数据归为一类，体现的是”同种中属性更接近的思想“，可是他受限于初始k的选择上；再从分类指标上来看，这些指标主要是用来衡量簇内、簇间划分程度，如果k越大，越多的样本可能”各自为政“，那么他们间的SP、CP和轮廓系数可知是越来越小，从这些指标代表的意义来说并不能准确的反映簇个数。

再者，人类认知上存在缺陷，我们认知我们所认知的，我们并不能直观的认知到客观规律，只能通过我们能感知到的一切来观测进而总结推理出客观规律，我们目前的知识都是”前人拿着测量工具和放大镜“一点点积累下来的，我们所思所想的都是实践的产物，工具、思想都是人类活动下的结晶，也就是说存在不足，可是却是我们能拿出手的”家当“。

在这里我主要想说的是在数据分析的时候不要太过迷信指标，特别是对一些不知真实分布的数据来做分析，如果这些指标能准确并一致的反映真实数据，那我们早就称霸宇宙，预测未来了。

回到之前的话题：我们统计分析的结果真的就和真实一样吗? 就目前来说，这些测量和分析方法是我们能拿出来的，随着人类的进步这些东西要么进化，要么淘汰。这些工具只是在一定程度上反映了真实而已，也许离得很近，也许大相径庭…至于最终的结果在没有真正认知到客观规律前，我们永远不知道，只是拿着我们人类活动的一系列产物来标榜而已，也许未来人类回首现在，也会觉得有趣吧。

到此这篇关于使用python实现kmean算法的文章就介绍到这了,更多相关Python实现kmean算法内容请搜索编程网以前的文章或继续浏览下面的相关文章希望大家以后多多支持编程网！

您可能感兴趣的文档:

--结束END--

本文标题: 使用python实现kmean算法

本文链接: https://lsjlt.com/news/211133.html(转载时请注明来源链接)

有问题或投稿请发送至: 邮箱/279061341@qq.com    QQ/279061341

猜你喜欢
  • 使用python实现kmean算法
    目录1. 简介2. kmean算法过程2.1 簇个数的选择2.2 聚类评价指标2.2.1 轮廓系数2.2.2 紧密性指标2.2.3 间隔性指标3. 代码4. 输出结果4.1 命令行输...
    99+
    2023-05-17
    python 算法 python实现kmean
  • 使用python实现rsa算法代码
    RSA算法是一种非对称加密算法，是现在广泛使用的公钥加密算法，主要应用是加密信息和数字签名。 维基百科给出的RSA算法简介如下： 假设Alice想要通过一个不可靠的媒体接收Bob的一条私人讯息。她可以用...
    99+
    2022-06-04
    算法 代码 python
  • 使用 Python 实现快速排序算法
    快速排序是一种高效的排序算法，它采用分治法的思想进行排序。在 Python 中，我们可以使用以下代码实现快速排序算法： def quick_sort(arr): if len(arr) ...
    99+
    2023-09-02
    排序算法 算法
  • 如何使用Python实现遗传算法
    本篇内容介绍了“如何使用Python实现遗传算法”的有关知识，在实际案例的操作过程中，不少人都会遇到这样的困境，接下来就让小编带领大家学习一下如何处理这些情况吧！希望大家仔细阅读，能够学有所成！遗传算法是模仿自然界生物进化机制发展起来的随机...
    99+
    2023-07-05
  • 用Python实现插值算法
            数模比赛中，常常需要对数据进行处理和分析，但有时候数据不多，就需要一些方法&ldquo...
    99+
    2024-04-02
  • 使用python怎么实现一个洗牌算法
    使用python怎么实现一个洗牌算法？相信很多没有经验的人对此束手无策，为此本文总结了问题出现的原因和解决方法，通过这篇文章希望你能解决这个问题。Python主要用来做什么Python主要应用于：1、Web开发；2、数据科学研究；3、网络爬...
    99+
    2023-06-14
  • 怎么使用Python实现冒泡排序算法
    这篇文章主要介绍“怎么使用Python实现冒泡排序算法”，在日常操作中，相信很多人在怎么使用Python实现冒泡排序算法问题上存在疑惑，小编查阅了各式资料，整理出简单好用的操作方法，希望对大家解答”怎么使用Python实现冒泡排序算法”的疑...
    99+
    2023-07-02
  • python实现dbscan算法
    DBSCAN 算法是一种基于密度的空间聚类算法。该算法利用基于密度的聚类的概念，即要求聚类空间中的一定区域内所包含对象(点或其它空间对象)的数目不小于某一给定阀值。DBSCAN 算法的显著优点是聚类速度快且能够有效处...
    99+
    2022-06-02
    python dbscan算法
  • python实现Simhash算法
    1、simhash步骤 simhash包含分词、hash、加权、合并、降维五大步骤 simhash代码如下： import jieba import jieba.analyse im...
    99+
    2024-04-02
  • Python实现LRU算法
    在第一节中已经实现了双向链表DoubleLinkedList类，本节我们基于双向链表实现LRU（Least Recently Used最近最少使用）缓存置换算法。Redis的淘汰机制...
    99+
    2024-04-02
  • kmp算法python实现
    kmp算法 kmp算法用于字符串的模式匹配，也就是找到模式字符串在目标字符串的第一次出现的位置比如abababc那么bab在其位置1处，bc在其位置5处我们首先想到的最简单的办法就是蛮力的一个字符一个字符的匹配，但那样的时间复杂度会是O...
    99+
    2023-01-31
    算法 kmp python
  • PageRank算法（python实现）
    Python 实现的PageRank算法，纯粹使用python原生模块，没有使用numpy、scipy。这个程序实现还比较原始，可优化的地方较多。 #-*- coding:utf-8 -*- import random N = 8 ...
    99+
    2023-01-31
    算法 PageRank python
  • LRU算法——python实现
    在LeetCode上看到这么一道题： Design and implement a data structure for Least Recently Used (LRU) cache. It should support the f...
    99+
    2023-01-31
    算法 LRU python
  • dijkstra算法python实现
    MAX_value = 999999 def dijkstra(graph, s): # 判断图是否为空，如果为空直接退出 if graph is None: return None dist ...
    99+
    2023-01-31
    算法 dijkstra python
  • 使用python实现估值计算
    在python中利蒙特卡洛公式实现估值计算，具体方法如下：from time import timefrom math import exp, sqrt, logfrom random import gauss, seedseed(2000...
    99+
    2024-04-02
  • 使用python实现两数之和的画解算法
    题目描述 给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target 的那 两个 整数，并返回它们的数组下标。 你可以假设每种输入只会对...
    99+
    2024-04-02
  • 使用Python实现图像融合及加法运算
    目录一.图像加法运算1.Numpy库加法2.OpenCV加法运算二.图像融合三.图像类型转换一.图像加法运算 1.Numpy库加法 其运算方法是：目标图像 = 图像1 + 图像2，运...
    99+
    2024-04-02
  • 使用Python实现遗传算法的完整代码
    目录遗传算法具体步骤：1.2 实验代码1.3 实验结果1.4 实验总结1、如何在算法中实现“优胜劣汰”？2 、如何保证进化一直是在正向进行？3、交叉如何实现？...
    99+
    2023-03-23
    Python 遗传算法 python算法
  • Python使用Numpy实现Kmeans算法的步骤详解
    目录Kmeans聚类算法介绍：1.聚类概念：2.Kmeans算法：定义：大概步骤：Kmeans距离测定方式：3.如何确定最佳的k值(类别数)：手肘法：python实现Kmeans算法...
    99+
    2024-04-02
  • 使用Python在实现一个梯度下降算法
    这期内容当中小编将会给大家带来有关使用Python在实现一个梯度下降算法，文章内容丰富且以专业的角度为大家分析和叙述，阅读完这篇文章希望大家可以有所收获。Python主要用来做什么Python主要应用于：1、Web开发；2、数据科学研究；3...
    99+
    2023-06-06
软考高级职称资格查询
热门wiki
近期文章
推荐阅读
热门问答
热门标签
编程网，编程工程师的家园，是目前国内优秀的开源技术社区之一，形成了由开源软件库、代码分享、资讯、协作翻译、讨论区和博客等几大频道内容，为IT开发者提供了一个发现、使用、并交流开源技术的平台。

  • 官方手机版

  • 微信公众号

  • 商务合作