Python 官方文档:入门教程 => 点击学习
目录连通域标记structure参数操作连通域定位连通域连通域标记 通过label函数,可以对数组中的连通区域进行标注,效果如下 from scipy.ndimage import
通过label函数,可以对数组中的连通区域进行标注,效果如下
from scipy.ndimage import label
import numpy as np
a = np.array([[0,0,1,1,0,0],
[0,0,0,1,0,0],
[1,1,0,0,1,0],
[0,0,0,1,0,0]])
labels, N = label(a)
print(labels)
'''
[[0 0 1 1 0 0]
[0 0 0 1 0 0]
[2 2 0 0 3 0]
[0 0 0 4 0 0]]
'''
print(N) 4
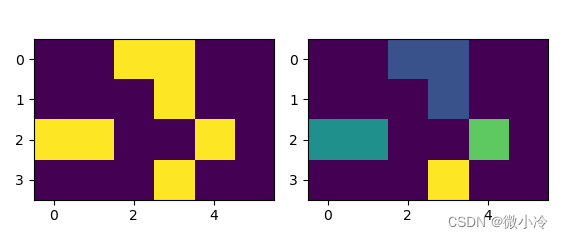
其中,a是一个二值矩阵,经过label标记后,其相连通的部分分别被标上了序号。可以更直观地用图像显示一下
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(121)
plt.imshow(a)
ax = fig.add_subplot(122)
plt.imshow(labels)
plt.show()
在label函数中,还有一个用于规范何为“连通”的参数,即structure,其数据类型为二值数组,其维度与输入的input相同。
在上面的示例中,连通域1,3,4尽管没有上下左右的联系,但在对角线上是有交集的,通过调整structure参数,可以提供一种将这三个区域连在一起的连通域方案。
stru = np.ones([3,3])
bLab, bN = label(a, stru)
print(bLab)
‘'‘
[[0 0 1 1 0 0]
[0 0 0 1 0 0]
[2 2 0 0 1 0]
[0 0 0 1 0 0]]
'‘'
可见,这次只选出了两组连通域。
scipy.ndimage提供了labeled_comprehension函数,其功能大致相当于[func(input[labels == i]) for i in index],即从已经做好连。通域标记的数组中,取出序号为index所在区域的值,参数如下
labeled_comprehension(input, labels, index, func, out_dtype, default, pass_positions=False)
其中input为输入数组;labels是已经做好的连通域标记;index为将要挑选进行操作的连通域序号;func为具体的操作函数;out_dtype为输出数据类型;default表示,当index不存在于连通域标记中时的输出值,下面做一个示例
from scipy.ndimage import labeled_comprehension
labeled_comprehension(a, labels, [1,2,3,4], sum, int, 0)
# array([3, 2, 1, 1])
连通域序号为1,2,3,4的区域,分别有3,2,1,1个元素,而且所有元素都是1,所以求和之后的值为[3, 2, 1, 1]。
scipy.ndimage中的find_objects函数可以返回连通域的切片范围。
from scipy.ndimage import find_objects
axis = find_objects(labels)
for x,y in axis:
print(x, y)
'''
slice(0, 2, None) slice(2, 4, None)
slice(2, 3, None) slice(0, 2, None)
slice(2, 3, None) slice(4, 5, None)
slice(3, 4, None) slice(3, 4, None)
''''
如果根据这个对原数组进行切片,就可以得到其对应的标记区域
for x,y in axis:
print(labels[x,y])
print("--------")
'''
[[1 1]
[0 1]]
--------
[[2 2]]
--------
[[3]]
--------
[[4]]
--------
'''
到此这篇关于python实现标记数组的连通域的文章就介绍到这了,更多相关Python标记数组连通域内容请搜索编程网以前的文章或继续浏览下面的相关文章希望大家以后多多支持编程网!
--结束END--
本文标题: Python实现标记数组的连通域
本文链接: https://lsjlt.com/news/210522.html(转载时请注明来源链接)
有问题或投稿请发送至: 邮箱/279061341@qq.com QQ/279061341
2024-03-01
2024-03-01
2024-03-01
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
回答
回答
回答
回答
回答
回答
回答
回答
回答
回答
0