Python 官方文档:入门教程 => 点击学习
利用numpy、matplotlib、sympy绘制sigmoid、tanh、ReLU、leaky ReLU、softMax函数 起因:深度学习途中,老师留一作业,绘制激活函数及其导
利用numpy、matplotlib、sympy绘制sigmoid、tanh、ReLU、leaky ReLU、softMax函数
起因:深度学习途中,老师留一作业,绘制激活函数及其导数,耗时挺久,记录学习过程
准备工作:下载numpy、matplotlib、sympy
pip install numpy matplotlib sympy
查找对应库的文档:
numpy文档 matplotlib文档 sympy文档
写代码的时候发现vscode不会格式化我的python?查了一下原来还要安装flake8和yapf,一个是检查代码规范工具一个是格式化工具,接着进行配置setting.JSON
"Python.linting.flake8Enabled": true, // 规范检查工具
"python.fORMatting.provider": "yapf", // 格式化工具
"python.linting.flake8Args": ["--max-line-length=248"], // 设置单行最长字符限制
"python.linting.pylintEnabled": false, // 关闭pylint工具
准备工作完成, 接下来就看看怎么写代码
第一步 新建一个py文件
先把激活函数的函数表达式写出来,这有两种方式,如果只是单纯的得出计算结果,其实用numpy就足够了,但是还要自己去求导,那就需要用sympy写出函数式了。
sympy表达函数的方式是这样的:
from sympy import symbols, evalf, diff
# 我们先要定义自变量是什么,这边按需求来,这是文档的例子有两个变量
x, y = symbols('x y')
# 然后我们写出函数表达式
expr = x + 2*y
# 输出看一下是什么东西
expr # x + 2*y
# 接着就要用我们定义的函数了
expr.evalf(subs={x: 10, y: 20}) # 50.000000
# 再对我们的函数求导
diff(expr, x, 1) # 对x进行求导得出结果 1,这也是表达式
diff为sympy的求导函数
sympy.core.function.diff(f, *symbols, **kwargs)
接着我们定义激活函数的表达式
def sigmoid():
"""
定义sigmoid函数
"""
x = symbols('x')
return 1. / (1 + exp(-x))
def tanh():
"""
定义tanh函数
"""
x = symbols('x')
return (exp(x) - exp(-x)) / (exp(x) + exp(-x))
def relu():
"""
定义ReLU函数
"""
x = symbols('x')
return Piecewise((0, x < 0), (x, x >= 0))
def leakyRelu():
"""
定义Leaky ReLu函数
"""
x = symbols('x')
return Piecewise((0.1 * x, x < 0), (x, x >= 0))
def softMax(x: np.ndarray):
"""
定义SoftMax函数\n
"""
exp_x = np.exp(x)
print(exp_x, np.sum(exp_x))
return exp_x / np.sum(exp_x)
def softmax_derivative(x):
"""
定义SoftMax导数函数\n
x - 输入x向量
"""
s = softMax(x)
return s * (1 - s)
然后再定义一个求导函数
def derivate(formula, len, variate):
"""
定义函数求导
formula:函数公式
len:求导次数
variate:自变量
"""
return diff(formula, variate, len)
这边有一个问题,为什么其他函数都是一个,而softMax函数有两个,一个是softMax函数定义,一个是其导函数定义?
我们看一下softMax函数的样子

softMax函数分母需要写累加的过程,使用numpy.sum无法通过sympy去求导(有人可以,我不知道为什么,可能是使用方式不同,知道的可以交流一下)而使用sympy.Sum或者sympy.summation又只能从i到n每次以1为单位累加
例如:假定有个表达式为 m**x (m的x次方)sympy.Sum(m**x, (x, 0, 100))则结果为m**100 + m**99 + m**98 … + m**1,而我定义的ndarray又是np.arange(-10, 10, 0.05),这就无法达到要求,就无法进行求导。
所以就写两个函数,一个是原函数定义,一个是导函数定义,并且之前也说了,如果是求值的话,其实只用numpy就可以完成。
至此,所有函数以及导函数就被我们定义好了
第二步 使用matplotlib绘制曲线
首先,我们得知道matplotlib有什么吧
matplotlib主要有Figure、Axes、Axis、Artist。我理解为figure就是画布,我们在绘制图形之前得准备好画布;axes和axis翻译都是轴的意思,但是axes应该是坐标轴,axis是坐标轴中的某一个轴;artist为其他可加入的元素
如果要绘制一张简单的图可以这样做
x = np.linspace(0, 2, 100) # Sample data.
# Note that even in the OO-style, we use `.pyplot.figure` to create the Figure.
fig, ax = plt.subplots(figsize=(5, 2.7), layout='constrained')
ax.plot(x, x, label='linear') # Plot some data on the axes.
ax.plot(x, x**2, label='quadratic') # Plot more data on the axes...
ax.plot(x, x**3, label='cubic') # ... and some more.
ax.set_xlabel('x label') # Add an x-label to the axes.
ax.set_ylabel('y label') # Add a y-label to the axes.
ax.set_title("Simple Plot") # Add a title to the axes.
ax.legend() # Add a legend.
然后我们准备绘制我们的函数曲线了
plt.xlabel('x label') // 两种方式加label,一种为ax.set_xlabel(面向对象),一种就是这种(面向函数)
plt.ylabel('y label')
加完laben之后 ,我考虑了两种绘制方式,一是把所有曲线都绘制在一个figure里面,但是分为不同的axes
使用subplot函数可以把figure分为2行2列的axes
plt.subplot(2, 2, 1, adjustable='box') # 1行1列
plt.subplot(2, 2, 2, adjustable='box') # 1行2列
第二个是通过输入函数名绘制指定的函数
do = input( 'input function expression what you want draw(sigmoid, tanh, relu, leakyRelu, softMax)\n' )
得到输入之后
try:
plt.xlabel('x label')
plt.ylabel('y label')
plt.title(do)
if (do == 'softMax'):
plt.plot(num, softMax(num), label='Softmax')
plt.plot(num, softmax_derivative(num), label='Softmax Derivative')
else:
plt.plot(
num,
[eval(f'{do}()').evalf(subs={symbols("x"): i}) for i in num])
plt.plot(num, [
derivate(eval(f'{do}()'), 1, 'x').evalf(subs={symbols('x'): i})
for i in num
])
plt.tight_layout()
plt.show()
except TypeError:
print(
'input function expression is wrong or the funciton is not configured'
)
这就完活了,附一张卖家秀
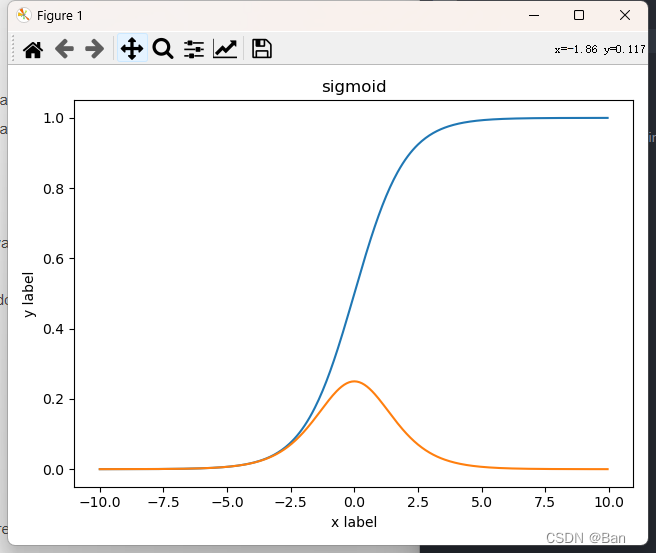
以上就是Python实现绘制多种激活函数曲线详解的详细内容,更多关于Python绘制激活函数曲线的资料请关注编程网其它相关文章!
--结束END--
本文标题: Python实现绘制多种激活函数曲线详解
本文链接: https://lsjlt.com/news/209993.html(转载时请注明来源链接)
有问题或投稿请发送至: 邮箱/279061341@qq.com QQ/279061341
2024-03-01
2024-03-01
2024-03-01
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
回答
回答
回答
回答
回答
回答
回答
回答
回答
回答
0