十个常用的损失函数解释以及Python代码实现

什么是损失函数？

损失函数是一种衡量模型与数据吻合程度的算法。损失函数测量实际测量值和预测值之间差距的一种方式。损失函数的值越高预测就越错误，损失函数值越低则预测越接近真实值。对每个单独的观测(数据点)计算损失函数。将所有损失函数（loss function）的值取平均值的函数称为代价函数（cost function），更简单的理解就是损失函数是针对单个样本的，而代价函数是针对所有样本的。

损失函数与度量指标

一些损失函数也可以被用作评价指标。但是损失函数和度量指标（metrics）有不同的目的。虽然度量指标用于评估最终模型并比较不同模型的性能，但损失函数在模型构建阶段用作正在创建的模型的优化器。损失函数指导模型如何最小化误差。

也就是说损失函数是知道模型如何训练的，而度量指标是说明模型的表现的。

为什么要用损失函数?

由于损失函数测量的是预测值和实际值之间的差距，因此在训练模型时可以使用它们来指导模型的改进(通常的梯度下降法)。在构建模型的过程中，如果特征的权重发生了变化得到了更好或更差的预测，就需要利用损失函数来判断模型中特征的权重是否需要改变，以及改变的方向。

我们可以在机器学习中使用各种各样的损失函数，这取决于我们试图解决的问题的类型、数据质量和分布以及我们使用的算法，下图为我们整理的10个常见的损失函数：

回归问题

1、均方误差(MSE)

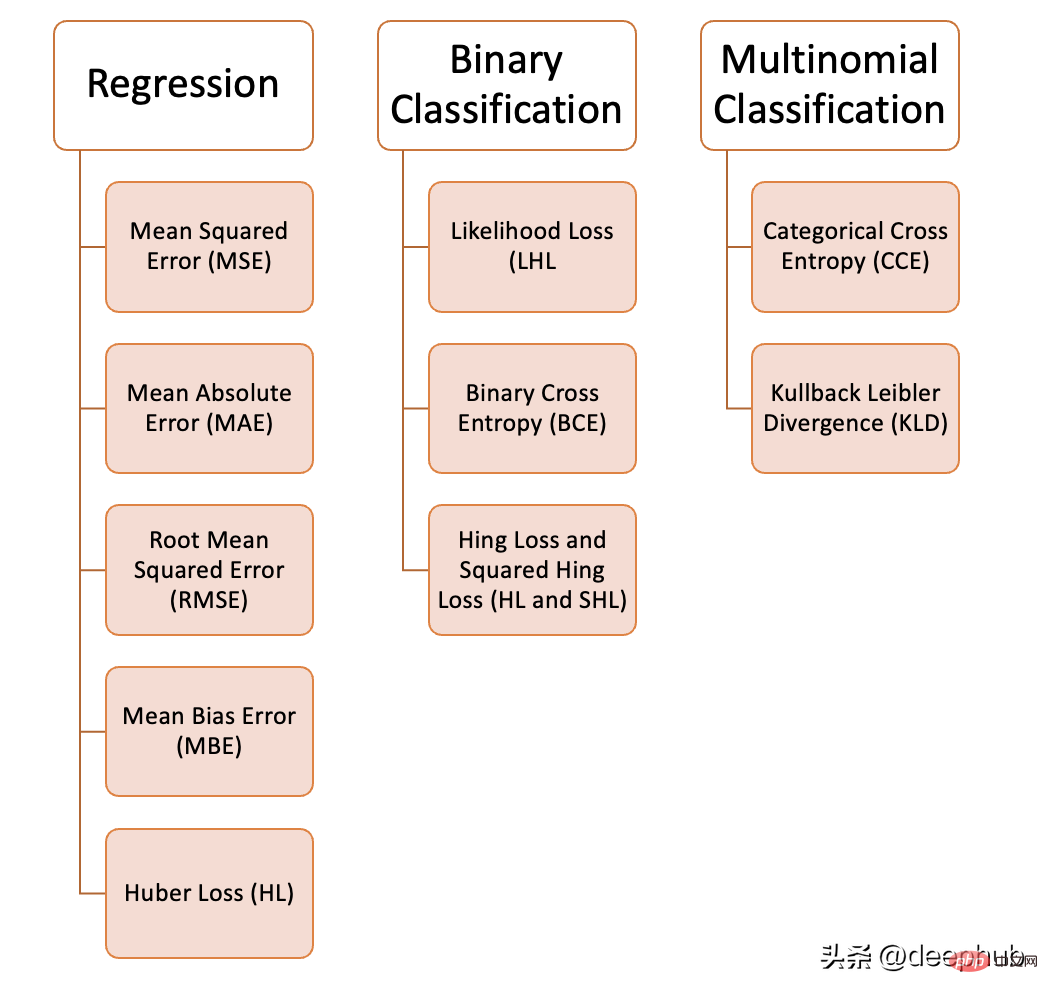
均方误差是指所有预测值和真实值之间的平方差，并将其平均值。常用于回归问题。

def MSE (y, y_predicted):sq_error = (y_predicted - y) ** 2sum_sq_error = np.sum(sq_error)mse = sum_sq_error/y.sizereturn mse

2、平均绝对误差(MAE)

作为预测值和真实值之间的绝对差的平均值来计算的。当数据有异常值时，这是比均方误差更好的测量方法。

def MAE (y, y_predicted):error = y_predicted - yabsolute_error = np.absolute(error)total_absolute_error = np.sum(absolute_error)mae = total_absolute_error/y.sizereturn mae

3、均方根误差(RMSE)

这个损失函数是均方误差的平方根。如果我们不想惩罚更大的错误，这是一个理想的方法。

def RMSE (y, y_predicted):sq_error = (y_predicted - y) ** 2total_sq_error = np.sum(sq_error)mse = total_sq_error/y.sizermse = math.sqrt(mse)return rmse

4、平均偏差误差(MBE)

类似于平均绝对误差但不求绝对值。这个损失函数的缺点是负误差和正误差可以相互抵消，所以当研究人员知道误差只有一个方向时，应用它会更好。

def MBE (y, y_predicted):error = y_predicted - ytotal_error = np.sum(error)mbe = total_error/y.sizereturn mbe

5、Huber损失

Huber损失函数结合了平均绝对误差(MAE)和均方误差(MSE)的优点。这是因为Hubber损失是一个有两个分支的函数。一个分支应用于符合期望值的MAE，另一个分支应用于异常值。Hubber Loss一般函数为：

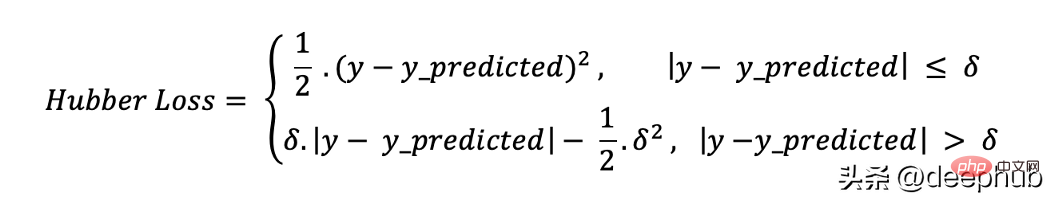
这里的

def hubber_loss (y, y_predicted, delta)delta = 1.35 * MAEy_size = y.sizetotal_error = 0for i in range (y_size):erro = np.absolute(y_predicted[i] - y[i])if error < delta:hubber_error = (error * error) / 2else:hubber_error = (delta * error) / (0.5 * (delta * delta))total_error += hubber_errortotal_hubber_error = total_error/y.sizereturn total_hubber_error

二元分类

6、最大似然损失(Likelihood Loss/LHL)

该损失函数主要用于二值分类问题。将每一个预测值的概率相乘,得到一个损失值，相关的代价函数是所有观测值的平均值。让我们用以下二元分类的示例为例，其中类别为[0]或[1]。如果输出概率等于或大于0.5，则预测类为[1]，否则为[0]。输出概率的示例如下：

[0.3 , 0.7 , 0.8 , 0.5 , 0.6 , 0.4]

对应的预测类为：

[0 , 1 , 1 , 1 , 1 , 0]

而实际的类为：

[0 , 1 , 1 , 0 , 1 , 0]

现在将使用真实的类和输出概率来计算损失。如果真类是[1]，我们使用输出概率，如果真类是[0]，我们使用1-概率：

((1–0.3)+0.7+0.8+(1–0.5)+0.6+(1–0.4)) / 6 = 0.65

python代码如下：

def LHL (y, y_predicted):likelihood_loss = (y * y_predicted) + ((1-y) * (y_predicted))total_likelihood_loss = np.sum(likelihood_loss)lhl = - total_likelihood_loss / y.sizereturn lhl

7、二元交叉熵(BCE)

这个函数是对数的似然损失的修正。对数列的叠加可以惩罚那些非常自信但是却错误的预测。二元交叉熵损失函数的一般公式为：

— (y . log (p) + (1 — y) . log (1 — p))

让我们继续使用上面例子的值：

输出概率= [0.3、0.7、0.8、0.5、0.6、0.4]

实际的类= [0，1，1，0，1，0]

— (0 . log (0.3) + (1–0) . log (1–0.3)) = 0.155

— (1 . log(0.7) + (1–1) . log (0.3)) = 0.155

— (1 . log(0.8) + (1–1) . log (0.2)) = 0.097

— (0 . log (0.5) + (1–0) . log (1–0.5)) = 0.301

— (1 . log(0.6) + (1–1) . log (0.4)) = 0.222

— (0 . log (0.4) + (1–0) . log (1–0.4)) = 0.222

那么代价函数的结果为：

(0.155 + 0.155 + 0.097 + 0.301 + 0.222 + 0.222) / 6 = 0.192

Python的代码如下：

def BCE (y, y_predicted):ce_loss = y*(np.log(y_predicted))+(1-y)*(np.log(1-y_predicted))total_ce = np.sum(ce_loss)bce = - total_ce/y.sizereturn bce

8、Hinge Loss 和 Squared Hinge Loss (HL and SHL)

Hinge Loss被翻译成铰链损失或者合页损失，这里还是以英文为准。

Hinge Loss主要用于支持向量机模型的评估。错误的预测和不太自信的正确预测都会受到惩罚。 所以一般损失函数是：

l(y) = max (0 , 1 — t . y)

这里的t是真实结果用[1]或[-1]表示。

使用Hinge Loss的类应该是[1]或[-1](不是[0])。为了在Hinge loss函数中不被惩罚，一个观测不仅需要正确分类而且到超平面的距离应该大于margin(一个自信的正确预测)。如果我们想进一步惩罚更高的误差，我们可以用与MSE类似的方法平方Hinge损失,也就是Squared Hinge Loss。

如果你对SVM比较熟悉，应该还记得在SVM中，超平面的边缘（margin）越高，则某一预测就越有信心。如果这块不熟悉，则看看这个可视化的例子:

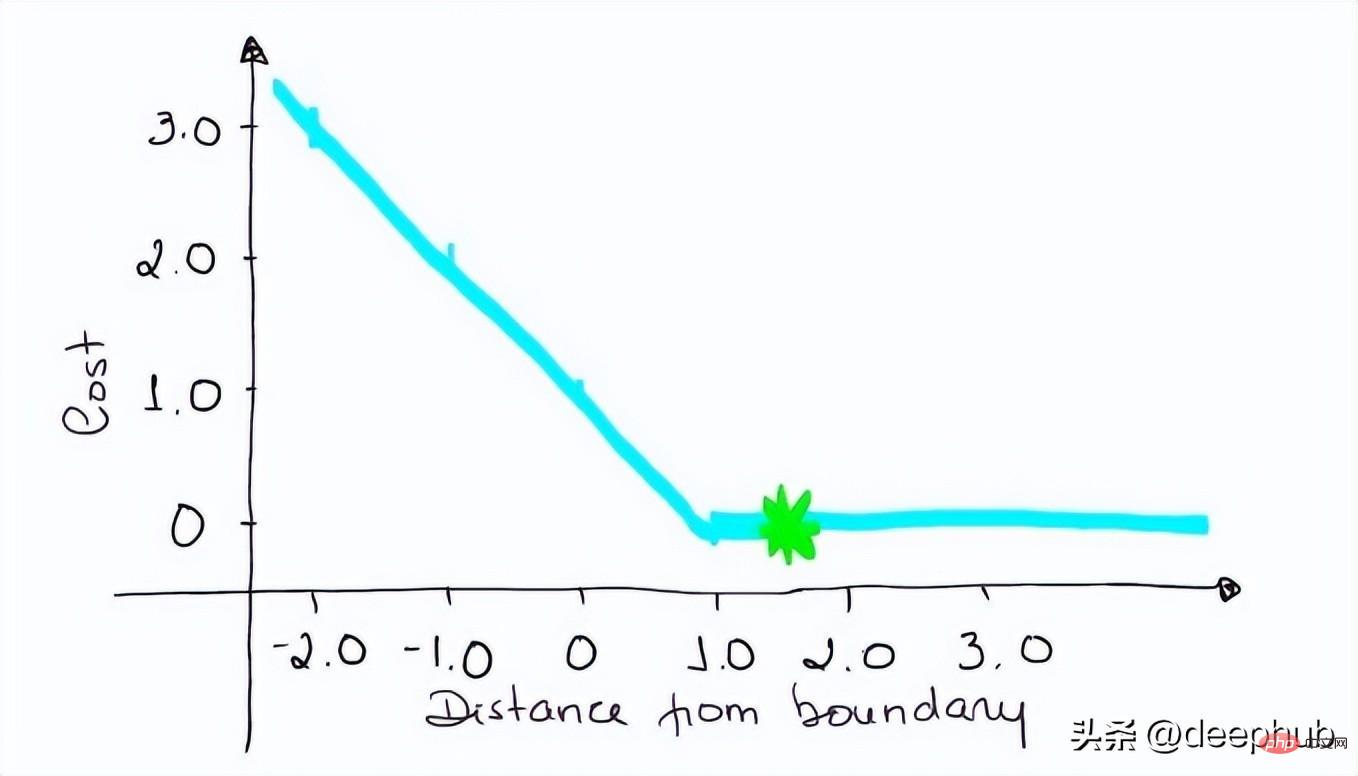
如果一个预测的结果是1.5，并且真正的类是[1]，损失将是0(零)，因为模型是高度自信的。

loss= Max (0,1 - 1* 1.5) = Max (0， -0.5) = 0

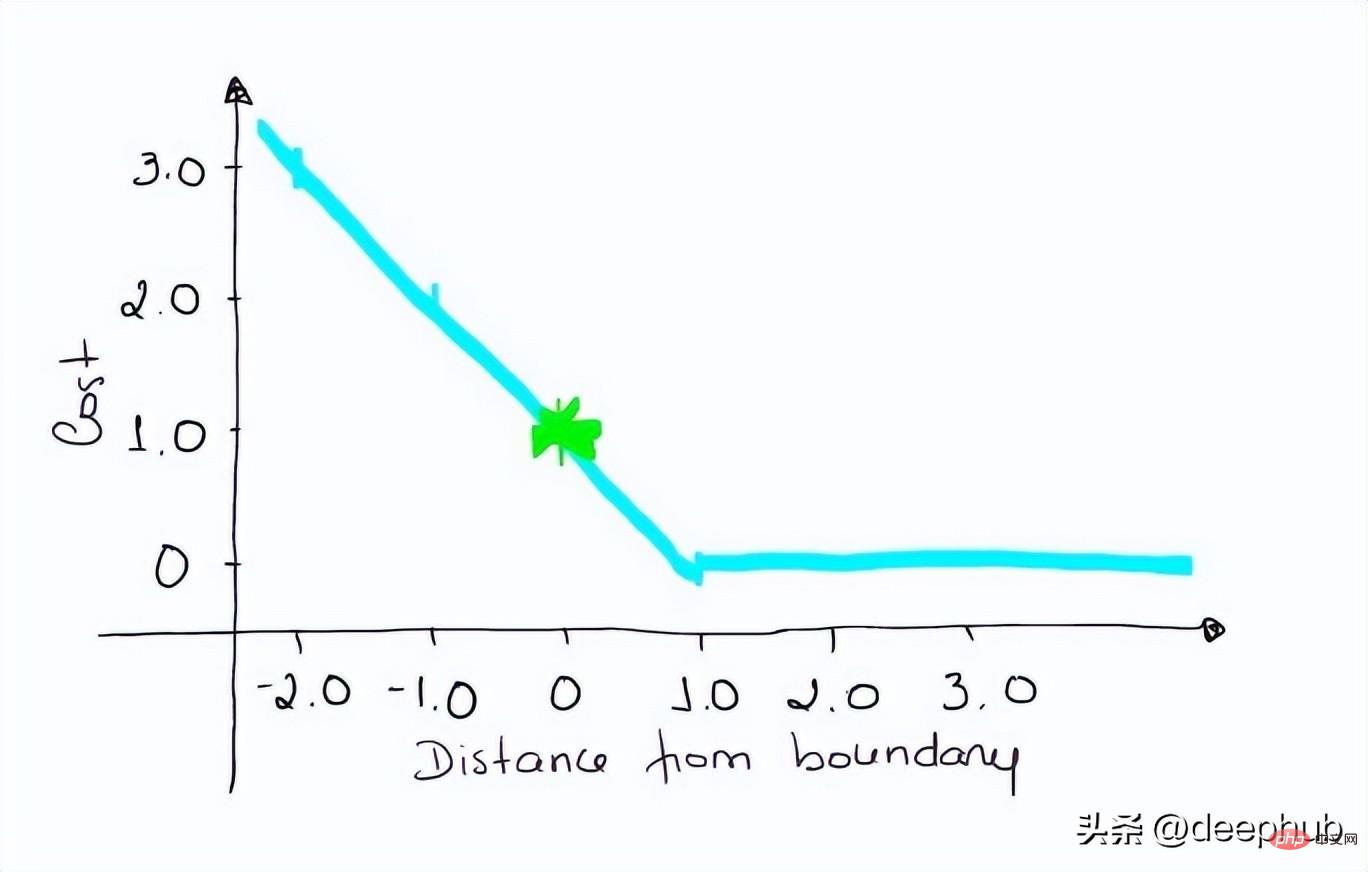
如果一个观测结果为0(0)，则表示该观测处于边界(超平面)，真实的类为[-1]。损失为1，模型既不正确也不错误，可信度很低。

loss = max (0 , 1–(-1) * 0) = max (0 , 1) = 1

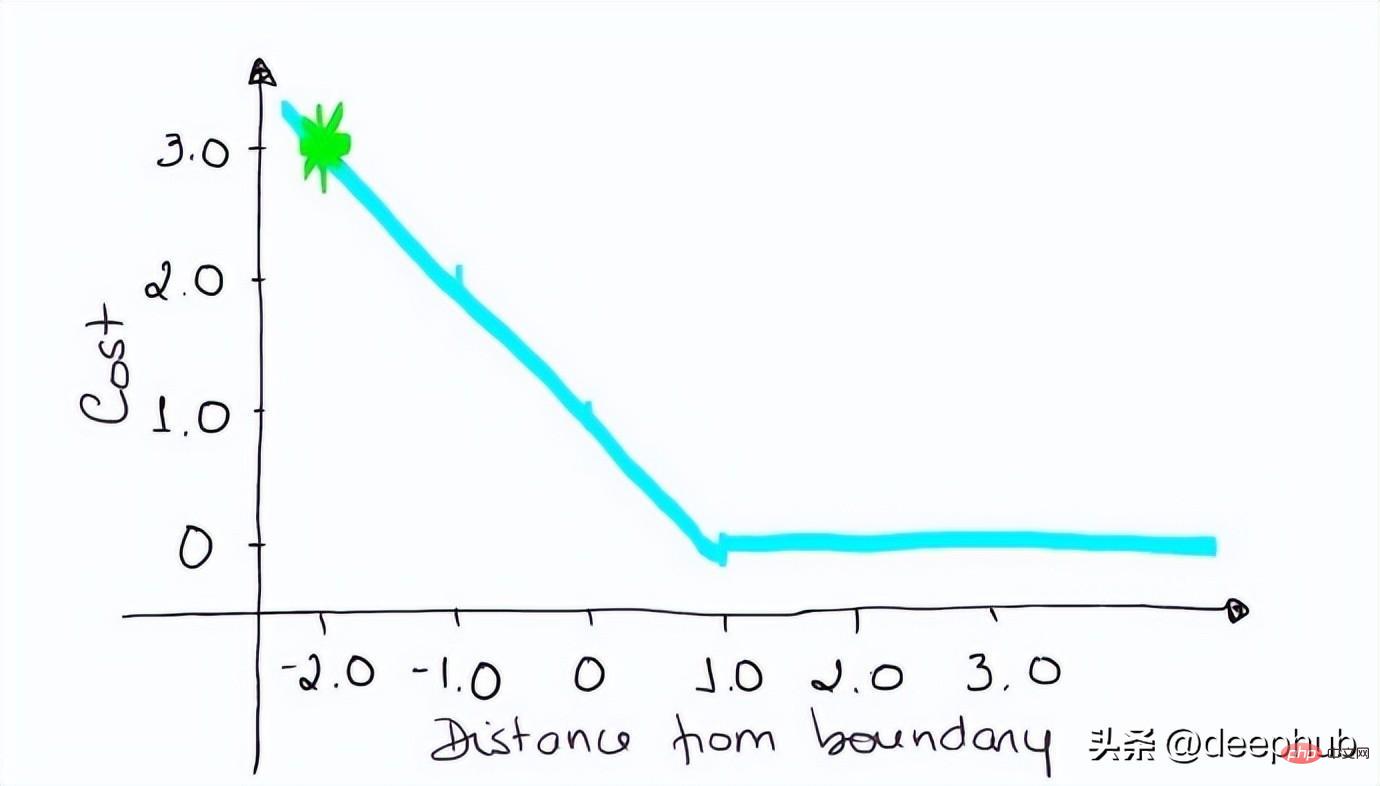
如果一次观测结果为2，但分类错误(乘以[-1])，则距离为-2。损失是3(非常高)，因为我们的模型对错误的决策非常有信心（这个是绝不能容忍的）。

loss = max (0 , 1 — (-1) . 2) = max (0 , 1+2) = max (0 , 3) = 3

python代码如下：

#Hinge Lossdef Hinge (y, y_predicted):hinge_loss = np.sum(max(0 , 1 - (y_predicted * y)))return hinge_loss#Squared Hinge Lossdef SqHinge (y, y_predicted):sq_hinge_loss = max (0 , 1 - (y_predicted * y)) ** 2total_sq_hinge_loss = np.sum(sq_hinge_loss)return total_sq_hinge_loss

多分类

9、交叉熵（CE）

在多分类中，我们使用与二元交叉熵类似的公式，但有一个额外的步骤。首先需要计算每一对[y, y_predicted]的损失，一般公式为：

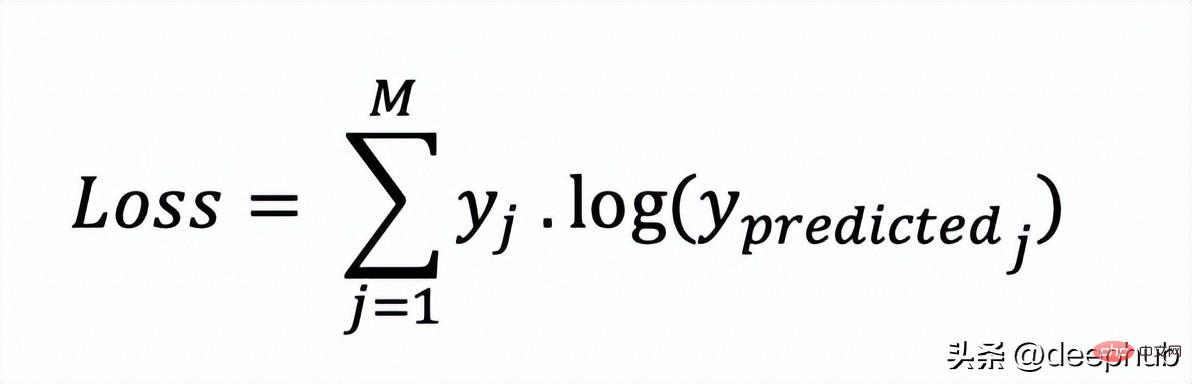
如果我们有三个类，其中单个[y, y_predicted]对的输出是：

这里实际的类3（也就是值=1的部分），我们的模型对真正的类是3的信任度是0.7。计算这损失如下：

Loss = 0 . log (0.1) + 0 . log (0.2) + 1 . log (0.7) = -0.155

为了得到代价函数的值，我们需要计算所有单个配对的损失，然后将它们相加最后乘以[-1/样本数量]。代价函数由下式给出：

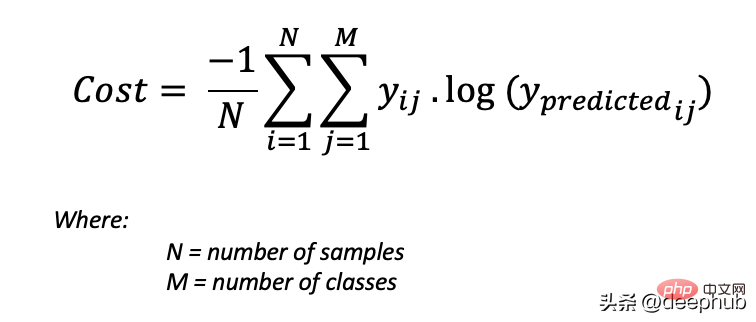
使用上面的例子，如果我们的第二对：

Loss = 0 . log (0.4) + 1. log (0.4) + 0. log (0.2) = -0.40

那么成本函数计算如下：

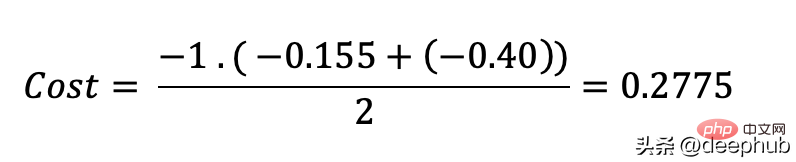
使用Python的代码示例可以更容易理解：

def CCE (y, y_predicted):cce_class = y * (np.log(y_predicted))sum_totalpair_cce = np.sum(cce_class)cce = - sum_totalpair_cce / y.sizereturn cce

10、Kullback-Leibler 散度 (KLD)

又被简化称为KL散度，它类似于分类交叉熵，但考虑了观测值发生的概率。 如果我们的类不平衡，它特别有用。

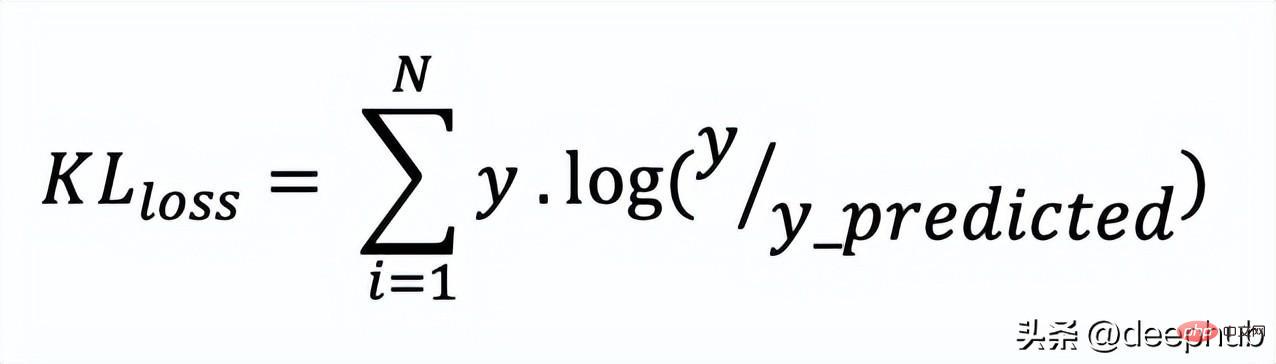
def KL (y, y_predicted):kl = y * (np.log(y / y_predicted))total_kl = np.sum(kl)return total_kl

以上就是常见的10个损失函数，希望对你有所帮助。

以上就是十个常用的损失函数解释以及Python代码实现的详细内容，更多请关注编程网其它相关文章！