C语言中关于树和二叉树的相关概念

树是一种 非线性的 数据结构，由 n(n >= 0) 个 有限节点 组成一种 具有层次关系 的集合

一、树

树的结构可以递归定义为：

根节点除根节点之外，其余节点被分成 M(M >= 0) 个互不相交的集合，每个集合分别是一棵子数

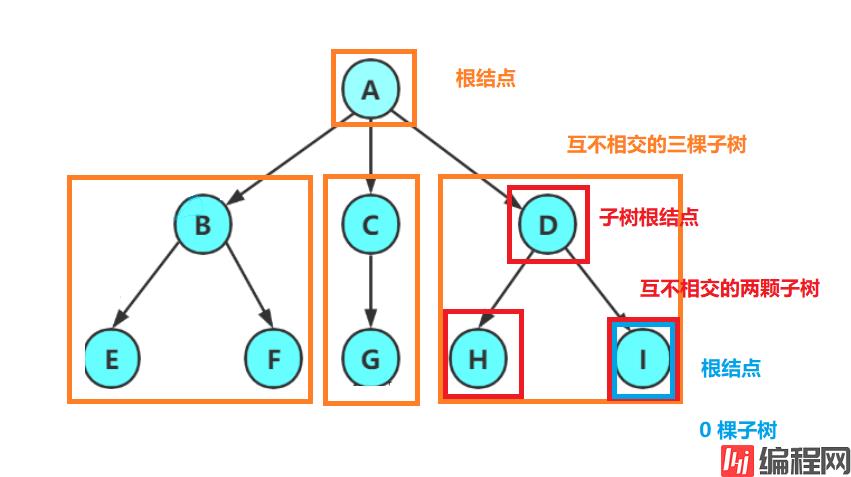
0 个结点的树就称为空树

• 树中除 根节点没有前驱节点 之外，其余每个节点都 有且仅有一个前驱节点，因此 n 个节点的树有 n - 1 条边
• 树中 每个节点 都可以 有 0 个或多个后继节点

树的相关概念

• 节点的度：节点含有的 子树个数，如图中 A 节点的度为 3
• 叶节点或终端节点：节点的 度为 0，如图中 E、F、G、H、I
• 分支节点或非终端节点：节点的 度不为 0，如图中 A、B、C、D
• 父节点或双亲节点：若一个节点含有子节点，则这个节点称为其子节点的父节点，如图中 B 是 E 和 F 的父节点
• 子节点或孩子节点：若一个节点含有子树，子树的根节点 称为该节点的子节点，如图中 E 和 F 都是 B 的子节点
• 兄弟节点：父节点相同 的节点互为兄弟节点，如图中 E 和 F 互为兄弟节点
• 树的度：树中所有节点的度中的最大值，如图中 A 节点的度为 3，是树中所有节点的度中的最大值，即树的度为 3
• 节点的层次：如上图，从根节点开始定义为第一层，根节点的子节点为第二层 …，(将根节点层次定义为 0 也是可以的)
• 树的高度或深度：树中节点的最大层次，图中为树的高度为 3
• 堂兄弟节点：父节点在同一层次的结点，如图中 E、F、G、H、I 结点互为堂兄弟节点
• 节点的祖先：根节点到该节点路径上的所有节点， A、B 结点是 E 的祖先
• 子孙：以某节点为根的子树中任一节点 都称为该节点的子孙，如上图：所有节点都是 A 的子孙

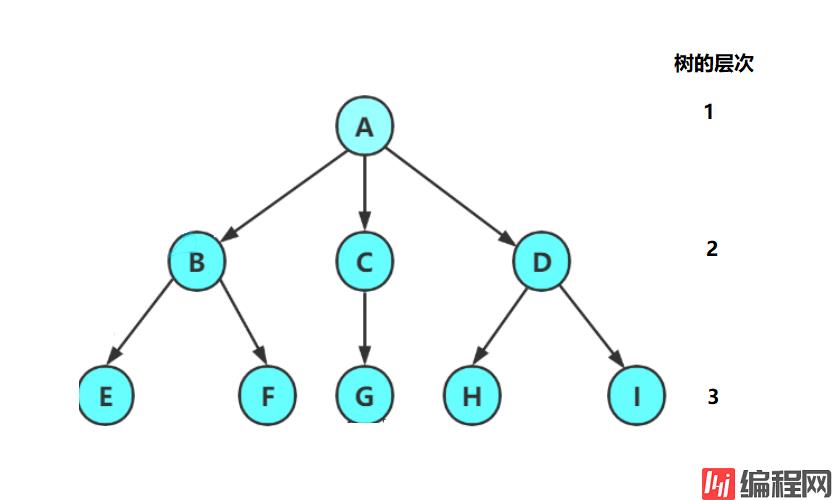
森林：由 M(M > 0) 棵 互不相交的树 构成的集合，将上图中 A 节点去掉后，便构成由以 B、C、D 为根节点的三颗树构成的森林

树的存储结构

在树的结构中可以发现，树是不易于用数组来存储的，因此 采用链式的方式来存储树

结构1:

由于树的结构中 每个节点的孩子个数是不确定的，因此每个节点需要使用一个顺序表存储孩子的指针

typedef int TreeDataType;
typedef struct Treenode
{
	TreeDataType data;
	SeqList childs;	//顺序表，并且每个元素的类型是 struct TreeNode*
}TreeNode;

结构2：

孩子兄弟表示法：节点的第一个孩子用该节点中的孩子指针指向，第二个孩子用该结点的第一个孩子结点的兄弟指针指向，第三个孩子用该节点的第二个孩子结点的兄弟指针指向…

typedef int TreeDataType;
typedef struct TreeNode
{
	TreeDataType data;
	struct TreeNode* child;
	struct TreeNode* brother;
}TreeNode;

存储树的方法还有双亲表示法，孩子表示法、孩子双亲表示法等，感兴趣的读者可以自行查阅

二、二叉树

树中 所有结点的度都小于等于 2 的树，即树的度小于等于 2 的树，称为二叉树

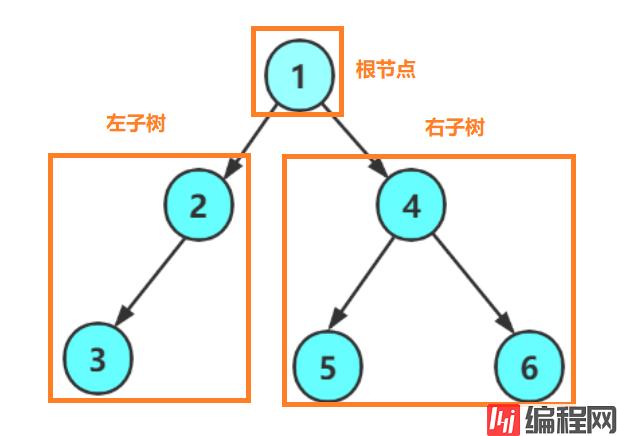
在二叉数中子树有左右区分，次序不能颠倒，左边的称为左子树，右边的称为右子树

二叉树的递归定义为：

• 根节点
• 左子树和右子树

左子树和右子树可以为空树，这里的子树也是一颗二叉树

二叉树的性质

假定根节点的层数为 1

• 一棵非空二叉树的第 i 层上最多有 2^(i - 1)个节点
• 深度为 h 的二叉树的最大节点数是 2^h - 1
• 任何一棵二叉树，如果度为 0 的叶节点个数为 n0，度为 2 的分支节点个数为 n2，则有 n0 ＝ n2 ＋1，即度为 0 的节点，比度为 2 的节点多 1

假设一颗二叉树有 n 个节点，度为 0 的节点数为 n0，度为 1 的节点数为 n1，度为 2 的节点数为 n2，根据 n 个节点的二叉树有 n - 1 条边，可得到如下关系：

• n0 * 0 + n1 * 1 + n2 * 2 = n - 1
• n0 + n1 + n2 = n

解得：n0 = n2 + 1

满二叉树：如果二叉树中每一个层的节点数都达到最大值，则这棵二叉树称为满二叉树

假设一棵二叉树的层数为 K，且节点总数是 2^K - 1，则它就是满二叉树

完全二叉树：假设一颗二叉树有 K 层，如果这颗二叉数的前 K - 1 层是满二叉树，并且第 K 层是从左往右还是连续的节点，则这棵二叉树称为完全二叉树

假设一棵完全二叉树的层数为 K ，则完全二叉树节点数的范围：2^(K - 1) ~ 2^K - 1

完全二叉树中度为 1 的节点有 0 个或 1 个

满二叉树可以认为是一种特殊的完全二叉树

• 具有 n 个节点的 满二叉树 的深度 h = log2(n + 1)，n 个节点的 完全二叉树 的深度 h = log2(n + 1)，h 向上取整(2.1 取 3)

• 对于具有 n 个节点的 完全二叉树，按照 从上至下、从左至右 的顺序，对所有节点从 0 开始依次编号

由于完全二叉树中从第二层开始，每一层的结点都是偶数个，因此 左孩子的编号都均为奇数，右孩子的编号都均为偶数

在 n 个节点的 完全二叉树 中，对于合法的编号为 i 的节点有：

• i 节点的 左孩子 的编号为 2 * i + 1，如果 2 * i + 1 < n，表示没有左孩子
• i 节点的 右孩子 的编号为 2 * i + 2，如果 2 * i + 2 < n，表示没有右孩子
• 根据 1 和 2 可知 i 节点的 父节点 的编号为 (i - 1) / 2，如果 i = 0，表示为根节点，没有父节点

到此这篇关于C语言中关于树和二叉树的相关概念的文章就介绍到这了,更多相关C语言树和二叉树内容请搜索编程网以前的文章或继续浏览下面的相关文章希望大家以后多多支持编程网！