首页 > 资讯 > 后端开发 > Python >PythonPSO算法处理TSP问题详解

279

分享到

PythonPSO算法处理TSP问题详解

Python PSO算法处理TSP Python PSO算法 Python TSP 2022-11-13 19:11:53 279人浏览泡泡鱼

Python 官方文档：入门教程 => 点击学习

摘要

目录前言PSO算法算法流程简单实现解决TSP数据表示区别完整代码特点分析设计环境压力设计压力策略强化学习前言先前我们给出了遗传算法的解决方案，那么同样的我们，给出使用PSO的解决方

前言

先前我们给出了遗传算法的解决方案，那么同样的我们，给出使用PSO的解决方案。其实对PSO算法比较了解的小伙伴应该是知道的，这个PSO其实是比较适合解决连续问题的。而我们的TSP问题显然是一个离散的问题。那么如何将连续问题转化为离散问题呢，那么这个时候其实有一个方案就是使用广义PSO算法。其实除了这个方案，我自己其实也有一个方案，这个方案基本上应该是通用的可以将连续问题转化为离散问题。这个方案的话，咱们在使用强化学习解决TSP问题的时候来搞定，值得一提的是，我也没有查阅相关文献，是我的一个改动吧，如果有，可以后面call我，拿出对应文献，我可以将这些东西进行优化。

PSO算法

那么开始之前，我们还是来聊聊基本的PSO算法。这个我写的非常多了，在这方面，因为暑假做的也是这方面的优化。核心就一个：

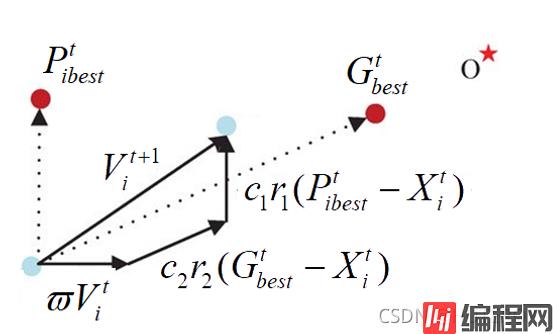
来我们来解释一下这个公式，你就懂了。

老规矩我们假设有一个方程 y=sin(x1)+cos(x2)

PSO算法通过模拟鸟类迁移来实现咱们的优化，这个怎么来的，就不说了，就说说这个核心。

我们刚刚的方程当中，有两个变量，x1,x2。由于是模拟鸟儿，所有为了实现瞎蒙大法，这里引入了速度的概念，x自然就是咱们的可行域，也就是解的空间。通过改变速度，来让x进行移动，也就是改变x的值。其中Pbest，表示这个鸟自己走过的位置里面最优的解，Gbest表示整个种群的最优解。什么意思，也就是说随着移动，这个鸟可能会走到更差的位置，因为和遗传不一样，他是不好的就干掉了，而这个不会。当然这里面涉及到很多局部问题，咱们这里都不讨论，没有哪一个算法是完美的，这个就对了。

算法流程

算法的主要流程：

第一步：对粒子群的随机位置和速度进行初始设定，同时设定迭代次数。

第二步：计算每个粒子的适应度值。

第三步：对每个粒子，将其适应度值与所经历的最好位置pbest i的适应度值进行比较，若较好，则将其作为当前的个体最优位置。

第四步：对每个粒子，将其适应度值与全局所经历的最好位置gbestg的适应度值进行比较，若较好，则将其作为当前的全局最优位置。

第五步：根据速度、位置公式对粒子的速度和位置进行优化，从而更新粒子位置。

第六步：如未达到结束条件（通常为最大循环数或最小误差要求），则返回第二步

优点：

PSO算法没有交叉和变异运算，依靠粒子速度完成搜索，并且在迭代进化中只有最优的粒子把信息传递给其它粒子，搜索速度快。

PSO算法具有记忆性，粒子群体的历史最好位置可以记忆并传递给其它粒子。

需调整的参数较少，结构简单，易于工程实现。

采用实数编码，直接由问题的解决定，问题解的变量数直接作为粒子的维数。

缺点：

缺乏速度的动态调节，容易陷入局部最优，导致收敛精度低和不易收敛。

不能有效解决离散及组合优化问题。

参数控制，对于不同的问题，如何选择合适的参数来达到最优效果。

不能有效求解一些非直角坐标系描述问题，

简单实现

ok,我们来看一下最简单的实现：

import numpy as np
import random
class PSO_model:
    def __init__(self,w,c1,c2,r1,r2,N,D,M):
        self.w = w # 惯性权值
        self.c1=c1
        self.c2=c2
        self.r1=r1
        self.r2=r2
        self.N=N # 初始化种群数量个数
        self.D=D # 搜索空间维度
        self.M=M # 迭代的最大次数
        self.x=np.zeros((self.N,self.D))  #粒子的初始位置
        self.v=np.zeros((self.N,self.D))  #粒子的初始速度
        self.pbest=np.zeros((self.N,self.D))  #个体最优值初始化
        self.gbest=np.zeros((1,self.D))  #种群最优值
        self.p_fit=np.zeros(self.N)
        self.fit=1e8 #初始化全局最优适应度
# 目标函数，也是适应度函数（求最小化问题）
    def function(self,x):
        A = 10
        x1=x[0]
        x2=x[1]
        Z = 2 * A + x1 ** 2 - A * np.cos(2 * np.pi * x1) + x2 ** 2 - A * np.cos(2 * np.pi * x2)
        return Z
     # 初始化种群
    def init_pop(self):
        for i in range(self.N):
            for j in range(self.D):
                self.x[i][j] = random.random()
                self.v[i][j] = random.random()
            self.pbest[i] = self.x[i] # 初始化个体的最优值
            aim=self.function(self.x[i]) # 计算个体的适应度值
            self.p_fit[i]=aim # 初始化个体的最优位置
            if aim < self.fit:  # 对个体适应度进行比较，计算出最优的种群适应度
                self.fit = aim
                self.gbest = self.x[i]
    # 更新粒子的位置与速度
    def update(self):
        for t in range(self.M): # 在迭代次数M内进行循环
            for i in range(self.N): # 对所有种群进行一次循环
                aim=self.function(self.x[i]) # 计算一次目标函数的适应度
                if aim<self.p_fit[i]: # 比较适应度大小，将小的负值给个体最优
                    self.p_fit[i]=aim
                    self.pbest[i]=self.x[i]
                    if self.p_fit[i]<self.fit: # 如果是个体最优再将和全体最优进行对比
                        self.gbest=self.x[i]
                        self.fit = self.p_fit[i]
            for i in range(self.N): # 更新粒子的速度和位置
                self.v[i]=self.w*self.v[i]+self.c1*self.r1*(self.pbest[i]-self.x[i])+ self.c2*self.r2*(self.gbest-self.x[i])
                self.x[i]=self.x[i]+self.v[i]
        print("最优值：",self.fit,"位置为：",self.gbest)
if __name__ == '__main__':
    # w,c1,c2,r1,r2,N,D,M参数初始化
    w=random.random()
    c1=c2=2#一般设置为2
    r1=0.7
    r2=0.5
    N=30
    D=2
    M=200
    pso_object=PSO_model(w,c1,c2,r1,r2,N,D,M)#设置初始权值
    pso_object.init_pop()
    pso_object.update()

解决TSP

数据表示

首先这个使用PSO的话，其实是和我们的这个先前使用遗传是类似的，我们依然通过一个矩阵表示种群，一个矩阵表示城市之间的距离。

      # 群体的初始化和路径的初始化
        self.population = np.array([0] * self.num_pop * self.num).reshape(
            self.num_pop, self.num)
        self.fitness = [0] * self.num_pop
        """
        计算城市的距离，我们用矩阵表示城市间的距离
        """
        self.__matrix_distance = self.__matrix_dis()

区别

和我们原来的PSO的最大区别是啥呢，其实和简单，在与我们速度的更新。我们在连续问题的时候其实是这样的：

同样的我们可以把X表示城市的编号，但是显然我们不能使用这种方案进行速度的更新。

那么这个时候，我们对于速度的更新的话，我们是需要使用到一种新的方案，那么这个方案的话其实就是套用遗传算算法的X更新。我们之所以需要速度说白了就是为了更新X，让X往好的方向进行瞎蒙。现在单纯使用速度更新是不行了，那么反正都是更新X，选择一个可以很好更新这个X的方案不就行了嘛。所以的话这里可直接使用遗传啊，我们的速度更新是参考Pbest和Gbest，之后按照一定的权重进行“学习”这样一来这个V就具备了Pbest和Gbest的一种“特征”。所以既然如此，那么我直接仿造遗传交叉的时候和Best进行交叉不就可以学习到一些对应的“特征”嘛。

    def cross_1(self, path, best_path):
        r1 = np.random.randint(self.num)
        r2 = np.random.randint(self.num)
        while r2 == r1:
            r2 = np.random.randint(self.num)
        left, right = min(r1, r2), max(r1, r2)
        cross = best_path[left:right + 1]
        for i in range(right - left + 1):
            for k in range(self.num):
                if path[k] == cross[i]:
                    path[k:self.num - 1] = path[k + 1:self.num]
                    path[-1] = 0
        path[self.num - right + left - 1:self.num] = cross
        return path

同时我们依然可以引入变异。

    def mutation(self,path):
        r1 = np.random.randint(self.num)
        r2 = np.random.randint(self.num)
        while r2 == r1:
            r2 = np.random.randint(self.num)
        path[r1],path[r2] = path[r2],path[r1]
        return path

完整代码

ok,现在我们来看到完整的代码：

import numpy as np
import matplotlib.pyplot as plt
class HybridPsoTSP(object):
    def __init__(self ,data ,num_pop=200):
        self.num_pop = num_pop  # 群体个数
        self.data = data        # 城市坐标
        self.num =len(data)     # 城市个数
        # 群体的初始化和路径的初始化
        self.population = np.array([0] * self.num_pop * self.num).reshape(
            self.num_pop, self.num)
        self.fitness = [0] * self.num_pop
        """
        计算城市的距离，我们用矩阵表示城市间的距离
        """
        self.__matrix_distance = self.__matrix_dis()
    def __matrix_dis(self):
        """
        计算14个城市的距离，将这些距离用矩阵存起来
        :return:
        """
        res = np.zeros((self.num, self.num))
        for i in range(self.num):
            for j in range(i + 1, self.num):
                res[i, j] = np.linalg.nORM(self.data[i, :] - self.data[j, :])
                res[j, i] = res[i, j]
        return res
    def cross_1(self, path, best_path):
        r1 = np.random.randint(self.num)
        r2 = np.random.randint(self.num)
        while r2 == r1:
            r2 = np.random.randint(self.num)
        left, right = min(r1, r2), max(r1, r2)
        cross = best_path[left:right + 1]
        for i in range(right - left + 1):
            for k in range(self.num):
                if path[k] == cross[i]:
                    path[k:self.num - 1] = path[k + 1:self.num]
                    path[-1] = 0
        path[self.num - right + left - 1:self.num] = cross
        return path
    def mutation(self,path):
        r1 = np.random.randint(self.num)
        r2 = np.random.randint(self.num)
        while r2 == r1:
            r2 = np.random.randint(self.num)
        path[r1],path[r2] = path[r2],path[r1]
        return path
    def comp_fit(self, one_path):
        """
        计算，咱们这个路径的长度，例如A-B-C-D
        :param one_path:
        :return:
        """
        res = 0
        for i in range(self.num - 1):
            res += self.__matrix_distance[one_path[i], one_path[i + 1]]
        res += self.__matrix_distance[one_path[-1], one_path[0]]
        return res
    def out_path(self, one_path):
        """
        输出我们的路径顺序
        :param one_path:
        :return:
        """
        res = str(one_path[0] + 1) + '-->'
        for i in range(1, self.num):
            res += str(one_path[i] + 1) + '-->'
        res += str(one_path[0] + 1) + '\n'
        print(res)
    def init_population(self):
        """
        初始化种群
        :return:
        """
        rand_ch = np.array(range(self.num))
        for i in range(self.num_pop):
            np.random.shuffle(rand_ch)
            self.population[i, :] = rand_ch
            self.fitness[i] = self.comp_fit(rand_ch)
def main(data, max_n=200, num_pop=200):
    Path_short = HybridPsoTSP(data, num_pop=num_pop)  # 混合粒子群算法类
    Path_short.init_population()  # 初始化种群
    # 初始化路径绘图
    fig, ax = plt.subplots()
    x = data[:, 0]
    y = data[:, 1]
    ax.scatter(x, y, linewidths=0.1)
    for i, txt in enumerate(range(1, len(data) + 1)):
        ax.annotate(txt, (x[i], y[i]))
    res0 = Path_short.population[0]
    x0 = x[res0]
    y0 = y[res0]
    for i in range(len(data) - 1):
        plt.quiver(x0[i], y0[i], x0[i + 1] - x0[i], y0[i + 1] - y0[i], color='r', width=0.005, angles='xy', scale=1,
                   scale_units='xy')
    plt.quiver(x0[-1], y0[-1], x0[0] - x0[-1], y0[0] - y0[-1], color='r', width=0.005, angles='xy', scale=1,
               scale_units='xy')
    plt.show()
    print('初始染色体的路程: ' + str(Path_short.fitness[0]))
    # 存储个体极值的路径和距离
    best_P_population = Path_short.population.copy()
    best_P_fit = Path_short.fitness.copy()
    min_index = np.argmin(Path_short.fitness)
    # 存储当前种群极值的路径和距离
    best_G_population = Path_short.population[min_index, :]
    best_G_fit = Path_short.fitness[min_index]
    # 存储每一步迭代后的最优路径和距离
    best_population = [best_G_population]
    best_fit = [best_G_fit]
    # 复制当前群体进行交叉变异
    x_new = Path_short.population.copy()
    for i in range(max_n):
        # 更新当前的个体极值
        for j in range(num_pop):
            if Path_short.fitness[j] < best_P_fit[j]:
                best_P_fit[j] = Path_short.fitness[j]
                best_P_population[j, :] = Path_short.population[j, :]
        # 更新当前种群的群体极值
        min_index = np.argmin(Path_short.fitness)
        best_G_population = Path_short.population[min_index, :]
        best_G_fit = Path_short.fitness[min_index]
        # 更新每一步迭代后的全局最优路径和解
        if best_G_fit < best_fit[-1]:
            best_fit.append(best_G_fit)
            best_population.append(best_G_population)
        else:
            best_fit.append(best_fit[-1])
            best_population.append(best_population[-1])
        # 将每个个体与个体极值和当前的群体极值进行交叉
        for j in range(num_pop):
            # 与个体极值交叉
            x_new[j, :] = Path_short.cross_1(x_new[j, :], best_P_population[j, :])
            fit = Path_short.comp_fit(x_new[j, :])
            # 判断是否保留
            if fit < Path_short.fitness[j]:
                Path_short.population[j, :] = x_new[j, :]
                Path_short.fitness[j] = fit
            # 与当前极值交叉
            x_new[j, :] = Path_short.cross_1(x_new[j, :], best_G_population)
            fit = Path_short.comp_fit(x_new[j, :])
            if fit < Path_short.fitness[j]:
                Path_short.population[j, :] = x_new[j, :]
                Path_short.fitness[j] = fit
            # 变异
            x_new[j, :] = Path_short.mutation(x_new[j, :])
            fit = Path_short.comp_fit(x_new[j, :])
            if fit <= Path_short.fitness[j]:
                Path_short.population[j] = x_new[j, :]
                Path_short.fitness[j] = fit
        if (i + 1) % 20 == 0:
            print('第' + str(i + 1) + '步后的最短的路程: ' + str(Path_short.fitness[min_index]))
            print('第' + str(i + 1) + '步后的最优路径:')
            Path_short.out_path(Path_short.population[min_index, :])  # 显示每一步的最优路径
    Path_short.best_population = best_population
    Path_short.best_fit = best_fit
    return Path_short  # 返回结果类
if __name__ == '__main__':
    data = np.array([16.47, 96.10, 16.47, 94.44, 20.09, 92.54,
                     22.39, 93.37, 25.23, 97.24, 22.00, 96.05, 20.47, 97.02,
                     17.20, 96.29, 16.30, 97.38, 14.05, 98.12, 16.53, 97.38,
                     21.52, 95.59, 19.41, 97.13, 20.09, 92.55]).reshape((14, 2))
    main(data)

初始染色体的路程: 71.30211569672313
第20步后的最短的路程: 29.340520066994223
第20步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第40步后的最短的路程: 29.340520066994223
第40步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第60步后的最短的路程: 29.340520066994223
第60步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第80步后的最短的路程: 29.340520066994223
第80步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第100步后的最短的路程: 29.340520066994223
第100步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第120步后的最短的路程: 29.340520066994223
第120步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第140步后的最短的路程: 29.340520066994223
第140步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第160步后的最短的路程: 29.340520066994223
第160步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第180步后的最短的路程: 29.340520066994223
第180步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第200步后的最短的路程: 29.340520066994223
第200步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9

可以看到收敛速度还是很快的。

特点分析

ok,到目前为止的话，我们介绍了两个算法去解决TSP或者是优化问题。我们来分析一下，这些算法有什么特点，为啥可以达到我们需要的优化效果。其实不管是遗传还是PSO，你其实都可以发现，有一个东西，我们可以暂且叫它环境压力。我们通过物竞天择，或者鸟类迁移，进行模拟寻优。而之所以需要这样做，是因为我们指定了一个规则，在我们的规则之下。我们让模拟的种群有一种压力去靠拢，其中物竞天择和鸟类迁移只是我们的一种手段，去应对这样的“压力”。所以的对于这种算法而言，最核心的点就两个：

设计环境压力

我们需要做优化问题，所以我们必须要能够让我们的解往那个方向走，需要一个驱动，需要一个压力。因此我们需要设计这样的一个环境，在遗传算法，粒子群算法是通过种群当中的生存，来进行设计的它的压力是我们的目标函数。由种群和目标函数（目标指标）构成了一个环境和压力。

设计压力策略

之后的话，我们设计好了一个环境和压力，那么未来应对这种压力，我们需要去设计一种策略，来应付这种压力。遗传算法是通过PUA自己，也就是种群的优胜略汰。PSO是通过学习，学习种群的优秀粒子和过去自己家的优秀“祖先”来应对这种压力的。

强化学习

所以的话，我们是否可以使用别的方案来实现这种优化效果。，在强化学习的算法框架里面的话，我们明确的知道了为什么他们可以实现优化，是环境压力+压力策略。恰好咱们强化学习是有环境的，适应函数和环境恰好可以组成环境+压力。本身的算法收敛过程就是我们的压力策略。所以我们完全是可以直接使用强化学习进行这个处理的。那么在这里咱们就来使用强化学习在下一篇文章当中。

到此这篇关于python PSO算法处理TSP问题详解的文章就介绍到这了,更多相关Python TSP内容请搜索编程网以前的文章或继续浏览下面的相关文章希望大家以后多多支持编程网！

您可能感兴趣的文档:

--结束END--

本文标题: PythonPSO算法处理TSP问题详解

本文链接: https://lsjlt.com/news/171185.html(转载时请注明来源链接)

有问题或投稿请发送至: 邮箱/279061341@qq.com QQ/279061341