Python 官方文档:入门教程 => 点击学习
目录前言拓扑排序介绍检测有向图中的环实现思路api设计代码实现基于深度优先的顶点排序实现思路API设计代码实现拓扑排序API设计代码实现测试验证前言 在现实生活中,我们经常会同一时间
在现实生活中,我们经常会同一时间接到很多任务去完成,但是这些任务的完成是有先后次序的。以我们学习java
学科为例,我们需要学习很多知识,但是这些知识在学习的过程中是需要按照先后次序来完成的。从Java基础,到
jsp/servlet,到SSM,到SpringBoot等是个循序渐进且有依赖的过程。在学习jsp前要首先掌握java基础和html基
础,学习ssm框架前要掌握jsp/servlet之类才行。

为了简化问题,我们使用整数为顶点编号的标准模型来表示这个案例:
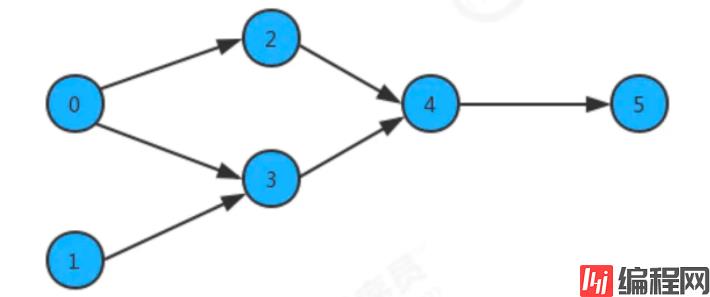
此时如果某个同学要学习这些课程,就需要指定出一个学习的方案,我们只需要对图中的顶点进行排序,让它转换为一个线性序列,就可以解决问题,这时就需要用到一种叫拓扑排序的算法。
给定一副有向图,将所有的顶点排序,使得所有的有向边均从排在前面的元素指向排在后面的元素,此时就可以明确的表示出每个顶点的优先级。下列是一副拓扑排序后的示意图:
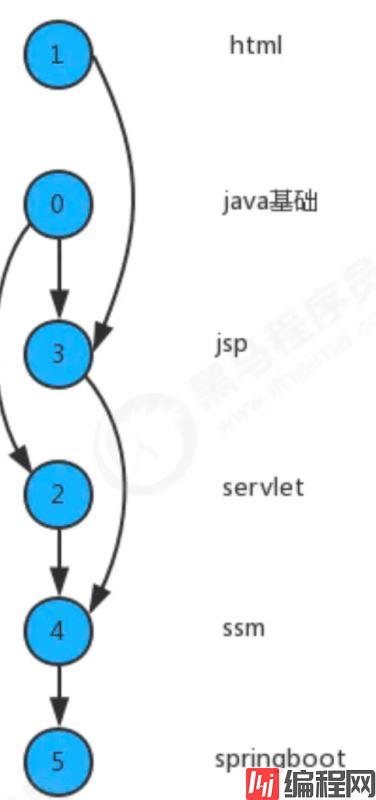
如果学习x课程前必须先学习y课程,学习y课程前必须先学习z课程,学习z课程前必须先学习x课程,那么一定是有问题了,我们就没有办法学习了,因为这三个条件没有办法同时满足。其实这三门课程x、y、z的条件组成了一个环:
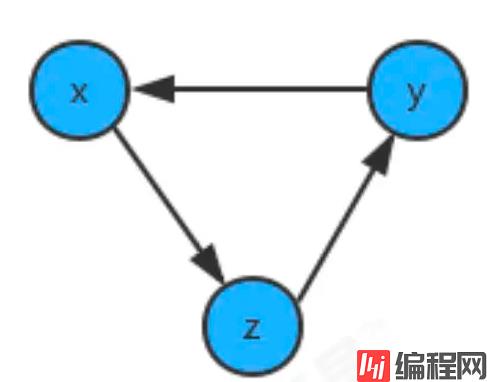
因此,如果我们要使用拓扑排序解决优先级问题,首先得保证图中没有环的存在。
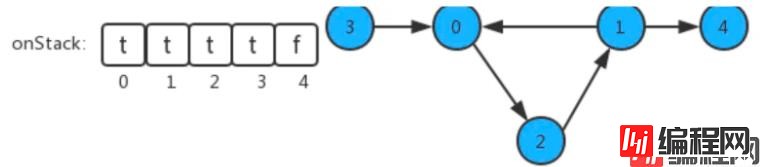
在API中添加了onStack[] 布尔数组,索引为图的顶点,当我们深度搜索时:
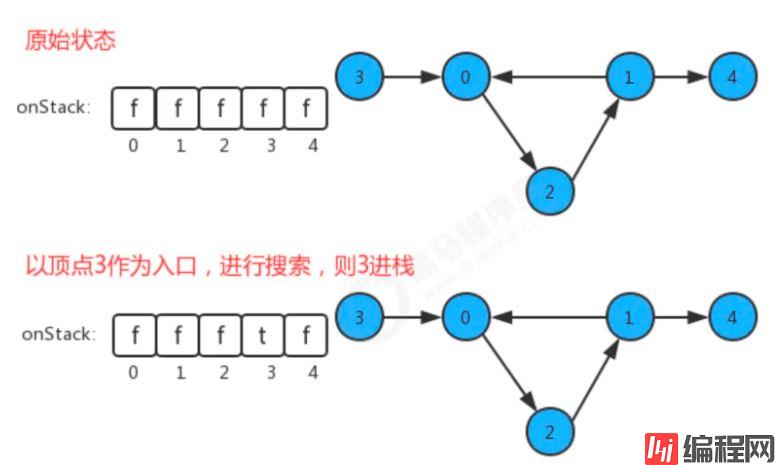



| 类名 | DirectedCycle |
|---|---|
| 成员变量 | 1.private boolean[] marked: 索引代表顶点,值表示当前顶点是否已经被搜索2.private boolean hasCycle: 记录图中是否有环3.private boolean[] onStack:索引代表顶点,使用栈的思想,记录当前顶点有没有已经处于正在搜索的有向路径上 |
| 构造方法 | DirectedCycle(Digraph G):创建一个检测环对象,检测图G中是否有环 |
| 成员方法 | 1.private void dfs(Digraph G,int v):基于深度优先搜索,检测图G中是否有环2.public boolean hasCycle():判断图中是否有环 |
public class DirectedCycle {
//索引代表顶点,值表示当前顶点是否已经被搜索
private boolean[] marked;
//记录图中是否有环
private boolean hasCycle;
//索引代表顶点,使用栈的思想,记录当前顶点有没有已经处于正在搜索的有向路径上
private boolean[] onStack;
//创建一个检测环对象,检测图G中是否有环
public DirectedCycle(Digraph G){
//初始化marked数组
this.marked = new boolean[G.V()];
//初始化hasCycle
this.hasCycle = false;
//初始化onStack数组
this.onStack = new boolean[G.V()];
//找到图中每一个顶点,让每一个顶点作为入口,调用一次dfs进行搜索
for (int v =0; v<G.V();v++){
//判断如果当前顶点还没有搜索过,则调用dfs进行搜索
if (!marked[v]){
dfs(G,v);
}
}
}
//基于深度优先搜索,检测图G中是否有环
private void dfs(Digraph G, int v){
//把顶点v表示为已搜索
marked[v] = true;
//把当前顶点进栈
onStack[v] = true;
for(Integer w: G.adj(v)) {
//判断如果当前顶点w没有被搜索过,则继续递归调用dfs方法完成深度优先搜索
if(!marked[w]) {
dfs(G, w);
}
//判断当前顶点w是否已经在栈中,如果已经在栈中,证明当前顶点之前处于正在搜索的状态,那么现在又要搜索一次,证明检测到环了
if (onStack[w]){
hasCycle = true;
return;
}
}
//把当前顶点出栈
onStack[v] = false;
}
//判断当前有向图G中是否有环
public boolean hasCycle(){
return hasCycle;
}
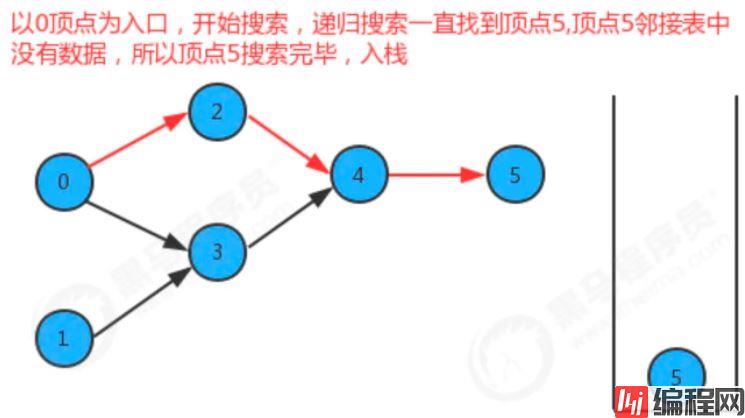
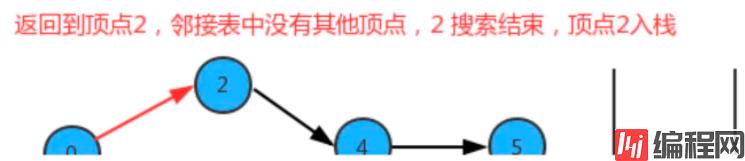
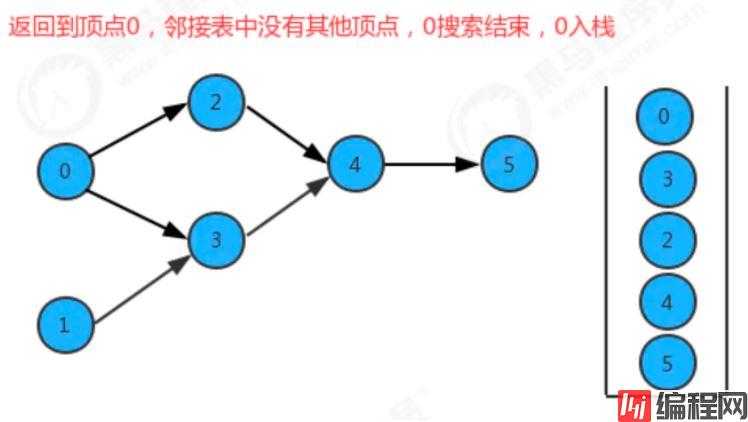
}如果要把图中的顶点生成线性序列其实是一件非常简单的事,之前我们学习并使用了多次深度优先搜索,我们会发现其实深度优先搜索有一个特点,那就是在一个连通子图上,每个顶点只会被搜索一次,如果我们能在深度优先搜索的基础上,添加一行代码,只需要将搜索的顶点放入到线性序列的数据结构中,我们就能完成这件事。
我们添加了一个栈reversePost用来存储顶点,当我们深度搜索图时,每搜索完毕一个顶点,把该顶点放入到reversePost中,这样就可以实现顶点排序。





| 类名 | DepthFirstOrder |
|---|---|
| 成员变量 | 1.private boolean[] marked: 索引代表顶点,值表示当前顶点是否已经被搜索2.private Stack reversePost: 使用栈,存储顶点序列 |
| 构造方法 | DepthFirstOrder(Digraph G):创建一个顶点排序对象,生成顶点线性序列; |
| 成员方法 | 1.private void dfs(Digraph G,int v):基于深度优先搜索,生成顶点线性序列2.public Stack reversePost():获取顶点线性序列 |
public class DepthFirstOrder {
//索引代表顶点,值表示当前顶点是否已经被搜索
private boolean[] marked;
//使用栈,存储顶点序列
private Stack<Integer> reversePost;
//创建一个检测环对象,检测图G中是否有环
public DepthFirstOrder(Digraph G){
//初始化marked数组
this.marked = new boolean[G.V()];
//初始化reversePost栈
this.reversePost = new Stack<>();
//遍历图中的每一个顶点,让每个顶点作为入口,完成一次深度优先搜索
for (int v = 0;v<G.V();v++){
if (!marked[v]){
dfs(G,v);
}
}
}
//基于深度优先搜索,把顶点排序
private void dfs(Digraph G, int v){
//标记当前v已经被搜索
marked[v] = true;
//通过循环深度搜索顶点v
for (Integer w : G.adj(v)) {
//如果当前顶点w没有搜索,则递归调用dfs进行搜索
if (!marked[w]){
dfs(G,w);
}
}
//让顶点v进栈
reversePost.push(v);
}
//获取顶点线性序列
public Stack<Integer> reversePost(){
return reversePost;
}
}前面已经实现了环的检测以及顶点排序,那么拓扑排序就很简单了,基于一幅图,先检测有没有环,如果没有环,则调用顶点排序即可。
| 类名 | TopoLogical |
|---|---|
| 成员变量 | 1.private Stack order: 顶点的拓扑排序 |
| 构造方法 | TopoLogical(Digraph G):构造拓扑排序对象 |
| 成员方法 | 1.public boolean isCycle():判断图G是否有环2.public Stack order():获取拓扑排序的所有顶点 |
public class TopoLogical {
//顶点的拓扑排序
private Stack<Integer> order;
//构造拓扑排序对象
public TopoLogical(Digraph G) {
//创建一个检测有向环的对象
DirectedCycle cycle = new DirectedCycle(G);
//判断G图中有没有环,如果没有环,则进行顶点排序:创建一个顶点排序对象
if (!cycle.hasCycle()){
DepthFirstOrder depthFirstOrder = new DepthFirstOrder(G);
order = depthFirstOrder.reversePost();
}
}
//判断图G是否有环
private boolean isCycle(){
return order==null;
}
//获取拓扑排序的所有顶点
public Stack<Integer> order(){
return order;
}
}public class TopoLogicalTest {
@Test
public void test() {
//准备有向图
Digraph digraph = new Digraph(6);
digraph.addEdge(0,2);
digraph.addEdge(0,3);
digraph.addEdge(2,4);
digraph.addEdge(3,4);
digraph.addEdge(4,5);
digraph.addEdge(1,3);
//通过TopoLogical对象堆有向图中的顶点进行排序
TopoLogical topoLogical = new TopoLogical(digraph);
//获取顶点的线性序列进行打印
Stack<Integer> order = topoLogical.order();
StringBuilder sb = new StringBuilder();
while (order.size() != 0) {
sb.append(order.pop()+"->");
};
String str = sb.toString();
int index = str.lastIndexOf("->");
str = str.substring(0,index);
System.out.println(str);
}
}
到此这篇关于Java数据结构之有向图的拓扑排序详解的文章就介绍到这了,更多相关Java有向图 拓扑排序内容请搜索编程网以前的文章或继续浏览下面的相关文章希望大家以后多多支持编程网!
--结束END--
本文标题: Java数据结构之有向图的拓扑排序详解
本文链接: https://lsjlt.com/news/170636.html(转载时请注明来源链接)
有问题或投稿请发送至: 邮箱/279061341@qq.com QQ/279061341
2024-03-01
2024-03-01
2024-03-01
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
回答
回答
回答
回答
回答
回答
回答
回答
回答
回答
0