Python 官方文档:入门教程 => 点击学习
目录前言抽象数据模型代码实现数据模型计算两个顶点之间路径算法总结前言 最近公司的项目上有个需求,还挺有分享价值的,这边做个记录。需求大致如下,下面的一个流程图,点击条件线上选择的内容
最近公司的项目上有个需求,还挺有分享价值的,这边做个记录。需求大致如下,下面的一个流程图,点击条件线上选择的内容,必须是前面配置过的节点,如果不是,需要在保存的时候做强校验提示。
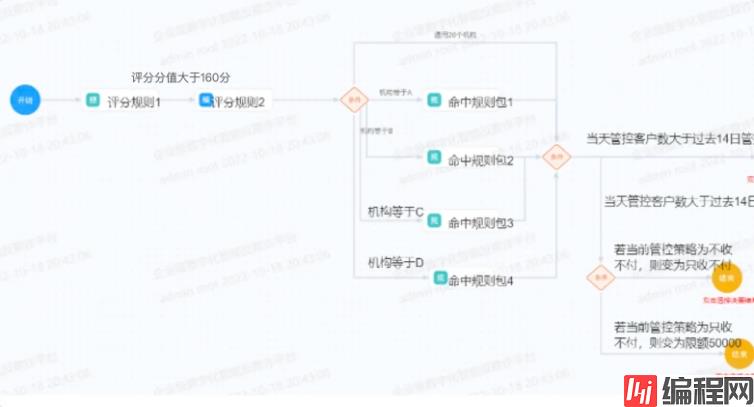
需求其实很明确,抽象出来就是获取图中两个顶点之间所有可达路径的顶点集合,大家可以思考下,该如何实现?这里面涉及到了数据结构中图相关知识,而数据结构算法也是本事最大的弱项,还是废了我一番工夫。
实际上,看到这个需求就很容易想到我们的有向图,那么在java中该用怎么样的数据结构表示有向图呢?在恶补了一番图相关的知识以后,最终确定用"邻接表"的方式实现。邻接表是图的一种最主要存储结构,用来描述图上的每一个点。
我们假设下面的一个有向图:
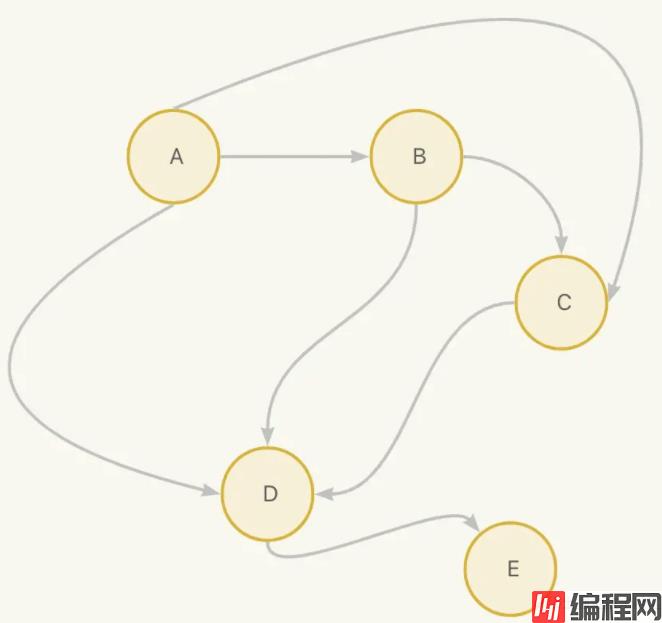
那么可以抽象出下面的数据结构:
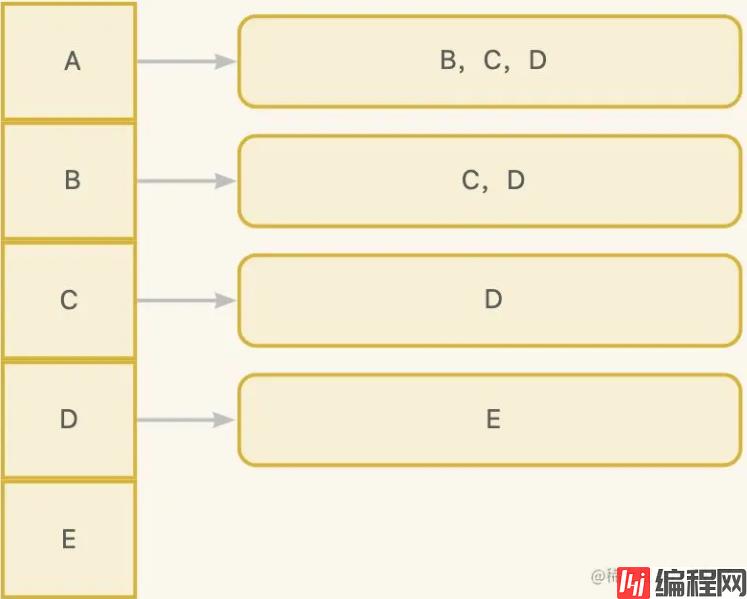
不知道大家发现规律了吗,每个顶点关联了它关联的其他顶点,比如A通过边关联了B,C,D, 可以理解为A有3条边,他们的目标顶点是B,C,D,那如何用java表示呢?
1.顶点类Vertex
@Data
@AllArgsConstructor
@Accessors(chain = true)
@NoArgsConstructor
class Vertex {
private String id;
private String name;
private List<Edge> edges = new ArrayList<>();
}成员变量edges表示顶点关联的所有的边
2.顶点关联的边类Edge
@Data
@AllArgsConstructor
@Accessors(chain = true)
@NoArgsConstructor
class Edge {
private String targetVertexId;
private String id;
private String name;
}成员变量targetVertexId用来存储边的目标顶点id
3.创建有向图DirectedDiagraph
@Data
@Slf4j(topic = "a.DirectedDiagraph")
public class DirectedDiagraph {
private Map<String, Vertex> vertextMap = new HashMap<>();
private int edgeNum;
public void addVertex(String vertexId, String vertexName) {
if (StrUtil.isEmpty(vertexId)) {
throw new RuntimeException("顶点id不能为空");
}
Vertex node = new Vertex().setId(vertexId).setName(vertexName);
// 添加到有向图中
vertextMap.put(vertexId, node);
}
public void addEdge(String fromVertexId, String targetVertexId, String edgeId, String edgeName) {
if (StrUtil.isEmpty(fromVertexId) || StrUtil.isEmpty(targetVertexId)) {
throw new RuntimeException("边的起始顶点或者目标顶点不能为空");
}
Edge edge = new Edge().setTargetVertexId(targetVertexId).setId(edgeId).setName(edgeName);
// 获取顶点
Vertex fromVertex = vertextMap.get(fromVertexId);
// 添加到边中
fromVertex.getEdges().add(edge);
// 边的数量+1
edgeNum++;
}
public void addEdge(String fromVertexId, String targetVertexId) {
this.addEdge(fromVertexId, targetVertexId, null, null);
}
public int getEdgeNum() {
return edgeNum;
}
}vertextMap存储图中的顶点信息addVertex() 方法用来添加顶点数据addEdge()方法用来添加边数据回到前言的需求,目前图的数据模型已经创建好了,现在需要实现计算两个顶点之间可达路径的所有顶点集合,直接上代码。
由于用到的参数比较多,这边封装了一个算法的类CalcTwoVertexPathlGorithm
calcPaths()方法就是算法的核心入口allPathList中存放了所有可达的路径列表。printAllPaths()方法打印所有的路径。getAllVertexs()返回所有可达的顶点集合。
@Slf4j(topic = "a.CalcTwoVertexPathlgorithm")
class CalcTwoVertexPathlgorithm {
private String fromVertexId;
private String toVertextId;
private DirectedDiagraph directedDiagraph;
private final List<List<String>> allPathList = new ArrayList<>();
public CalcTwoVertexPathlgorithm(DirectedDiagraph directedDiagraph, String fromVertexId, String toVertextId) {
this.fromVertexId = fromVertexId;
this.toVertextId = toVertextId;
this.directedDiagraph = directedDiagraph;
}
public void printAllPaths() {
log.info("the path betweent {} and {}:", fromVertexId, toVertextId);
allPathList.forEach(item -> {
log.info("{}", item);
});
}
public Set<String> getAllVertexs() {
return allPathList.stream().flatMap(Collection::stream).collect(Collectors.toSet());
}
public void calcPaths() {
// 先清理之前调用留下的数据
allPathList.clear();
DirectedDiagraph.Vertex fromNode = directedDiagraph.getVertextMap().get(fromVertexId);
DirectedDiagraph.Vertex toNode = directedDiagraph.getVertextMap().get(toVertextId);
// 无法找到边
if (fromNode == null || toNode == null) {
throw new RuntimeException("顶点id不存在");
}
// 如果其实节点等于目标节点,则也作为一个边
if (fromNode == toNode) {
List<String> paths = new ArrayList<>();
paths.add(fromVertexId);
allPathList.add(paths);
return;
}
// 递归调用
coreRecGetAllPaths(fromNode, toNode, new ArrayDeque<>());
}
private void coreRecGetAllPaths(DirectedDiagraph.Vertex fromVertex, DirectedDiagraph.Vertex toVertex, Deque<String> nowPaths) {
// 检查是否存在环,跳过
if (nowPaths.contains(fromVertex.getId())) {
System.out.println("存在环");
// 出栈
nowPaths.pop();
return;
}
// 当前路径加上其实节点
nowPaths.push(fromVertex.getId());
// 深度搜索边
for (DirectedDiagraph.Edge edge : fromVertex.getEdges()) {
// 如果边的目标顶点和路径的最终节点一直,表示找到成功
if (StrUtil.equals(edge.getTargetVertexId(), toVertex.getId())) {
// 将数据添加到当前路径中
nowPaths.push(toVertex.getId());
// 拷贝一份数据放到allPathList中
List<String> findPaths = new ArrayList<>();
findPaths.addAll(nowPaths);
CollUtil.reverse(findPaths);
allPathList.add(findPaths);
// 加入了最终节点,返回一次
nowPaths.pop();
// 跳过,查询下一个边
continue;
}
// 以边的目标顶点作为其实顶点,继续搜索
DirectedDiagraph.Vertex nextFromVertex = directedDiagraph.getVertextMap().get(edge.getTargetVertexId());
if (nextFromVertex == null) {
throw new RuntimeException("顶点id不存在");
}
// 递归调用下一次
coreRecGetAllPaths(nextFromVertex, toVertex, nowPaths);
}
// 结束了,没找到,弹出数据
nowPaths.pop();
}代码注释比较清晰的,就不再介绍了,主要是利用了深度搜索的方式+ 栈保存临时路径。
然后在DirectedDiagraph类中添加一个方法findAllPaths(),查找所有的路径,如下图:
@Data
@Slf4j(topic = "a.DirectedDiagraph")
public class DirectedDiagraph {
.....
public Set<String> findAllPaths(String fromVertexId, String targetVertexId) {
CalcTwoVertexPathlgorithm calcTwoVertexPathlgorithm = new CalcTwoVertexPathlgorithm(this, fromVertexId, targetVertexId);
// 先计算
calcTwoVertexPathlgorithm.calcPaths();
// 打印找到的路径
calcTwoVertexPathlgorithm.printAllPaths();
// 然后返回所有的内容
return calcTwoVertexPathlgorithm.getAllVertexs();
}
....
}最后,我们写个单元测试验证下吧。
@Test
public void test1() {
DirectedDiagraph directedDiagraph = new DirectedDiagraph();
directedDiagraph.addVertex("A", "A");
directedDiagraph.addVertex("B", "B");
directedDiagraph.addVertex("C", "C");
directedDiagraph.addVertex("D", "D");
directedDiagraph.addVertex("E", "E");
directedDiagraph.addEdge("A", "B");
directedDiagraph.addEdge("B", "C");
directedDiagraph.addEdge("C", "D");
directedDiagraph.addEdge("A", "D");
directedDiagraph.addEdge("B", "D");
directedDiagraph.addEdge("A", "C");
directedDiagraph.addEdge("D", "E");
Set<String> allPaths = directedDiagraph.findAllPaths("A", "D");
log.info("all vertexIds: {}", allPaths);
}创建的例子也是我们前面图片中的例子,我们看下运行结果是否符合预期。
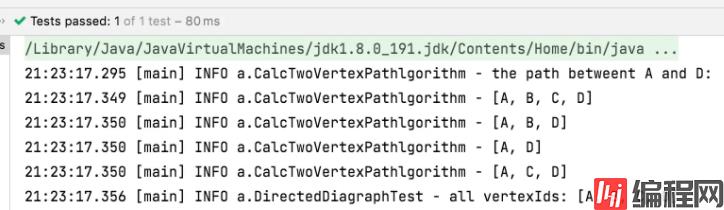
本次需求利用了图这个数据结构得到结果,突然感觉数据结构和算法真的很重要,感觉现在的做法也不是最优解,性能应该也不是最佳,但是考虑到流程节点数据不会很多,应该能满足业务需求。不知道大家有没有更好的做法呢?
以上就是Java实现计算图中两个顶点的所有路径的详细内容,更多关于Java计算顶点所有路径的资料请关注编程网其它相关文章!
--结束END--
本文标题: Java实现计算图中两个顶点的所有路径
本文链接: https://lsjlt.com/news/170223.html(转载时请注明来源链接)
有问题或投稿请发送至: 邮箱/279061341@qq.com QQ/279061341
2024-03-01
2024-03-01
2024-03-01
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
回答
回答
回答
回答
回答
回答
回答
回答
回答
回答
0