首页 > 资讯 > 后端开发 > Python >详解Java中二分法的基本思路和实现

148

分享到

详解Java中二分法的基本思路和实现

2024-04-02 19:04:59 148人浏览泡泡鱼

Python 官方文档：入门教程 => 点击学习

摘要

目录在一个有序数组中，找某个数是否存在在一个有序数组中，找大于等于某个数最左侧的位置在排序数组中查找元素的第一个和最后一个位置局部最大值问题在一个有序数组中，找某个数是否存在思路

在一个有序数组中，找某个数是否存在

思路：

由于是有序数组，可以先得到中点位置，中点可以把数组分为左右半边。
如果中点位置的值等于目标值，直接返回中点位置。
如果中点位置的值小于目标值，则去数组中点左侧按同样的方式寻找。
如果中点位置的值大于目标值，则取数组中点右侧按同样的方式寻找。
如果最后没有找到，则返回：-1。

代码

class Solution {
    public int search(int[] arr, int t) {
        if (arr == null || arr.length < 1) {
            return -1;
        }
        int l = 0;
        int r = arr.length - 1;
        while (l <= r) {
            int m = l + ((r - l) >> 1);
            if (arr[m] == t) {
                return m;
            } else if (arr[m] > t) {
                r = m - 1;
            } else {
                l = m + 1;
            }
        }
        return -1;
    }
}

时间复杂度 O(logN)。

在一个有序数组中，找大于等于某个数最左侧的位置

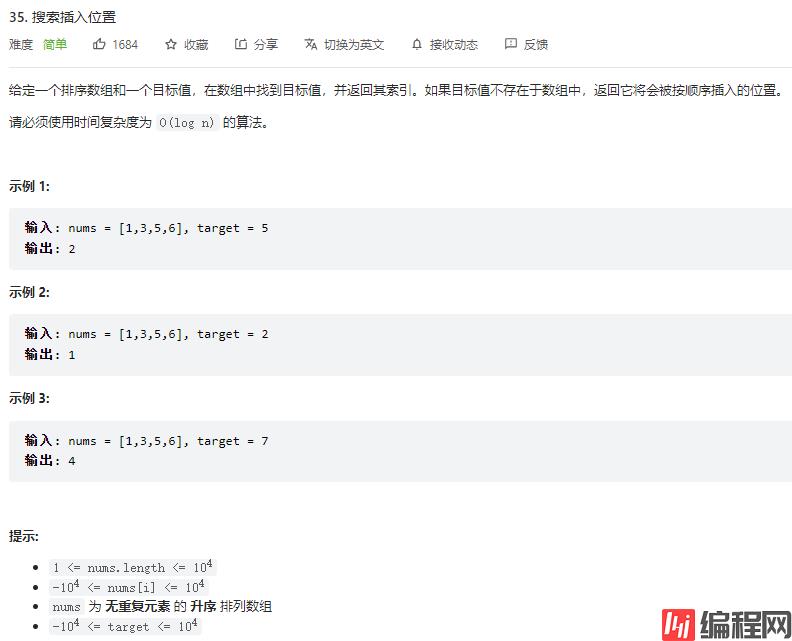
示例 1:

输入: nums = [1,3,5,6], target = 5

输出: 2

说明：如果要在num这个数组中插入 5 这个元素，应该是插入在元素 3 和元素 5 之间的位置，即 2 号位置。

示例 2:

输入: nums = [1,3,5,6], target = 2

输出: 1

说明：如果要在num这个数组中插入 2 这个元素，应该是插入在元素 1 和元素 3 之间的位置，即 1 号位置。

示例 3:

输入: nums = [1,3,5,6], target = 7

输出: 4

说明：如果要在num这个数组中插入 7 这个元素，应该是插入在数组末尾，即 4 号位置。

通过上述示例可以知道，这题本质上就是求在一个有序数组中，找大于等于某个数最左侧的位置，如果不存在，就返回数组长度（表示插入在最末尾位置）

我们只需要在上例基础上进行简单改动即可，上例中，我们找到满足条件的位置就直接return了

if (arr[m] == t) {
    return m;
}

在本问题中，因为要找到最左侧的位置，所以，在遇到相等的时候，只需要先把位置记录下来，不用直接返回，然后继续去左侧找是否还有满足条件的更左边的位置。

同时，在遇到arr[m] > t条件下，也需要记录下此时的m位置，因为这也可能是满足条件的位置。

代码：

class Solution {
    public static int searchInsert(int[] arr, int t) {
        int ans = arr.length;
        int l = 0;
        int r = arr.length - 1;
        while (l <= r) {
            int m = l + ((r - l)>>1);
            if (arr[m] >= t) {
                ans = m;
                r = m - 1;
            } else  {
                l = m + 1;
            } 
        }
        return ans;
    }
}

整个算法的时间复杂度是O(logN)。

在排序数组中查找元素的第一个和最后一个位置

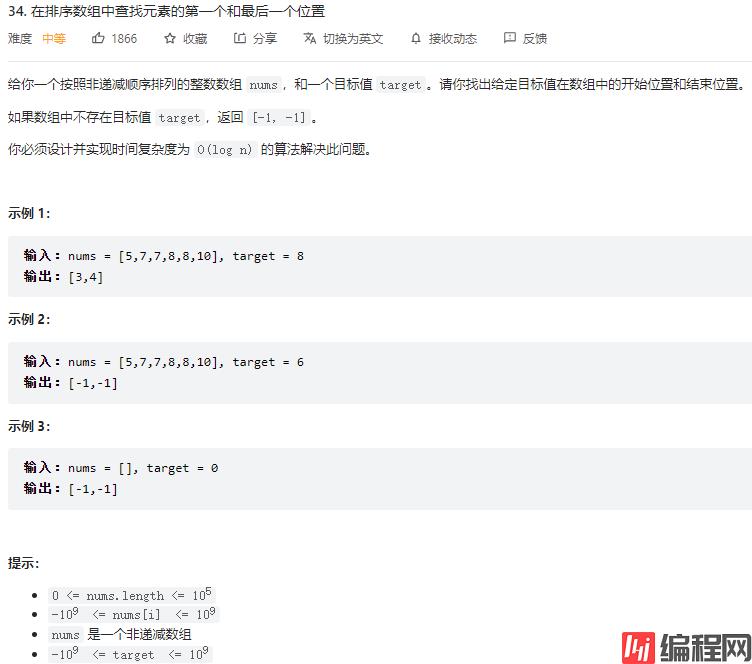
思路

本题也是用二分来解，当通过二分找到某个元素的时候，不急着返回，而是继续往左（右）找，看能否找到更左（右）位置匹配的值。

代码如下：

class Solution {
    public static int[] searchRange(int[] arr, int t) {
        if (arr == null || arr.length < 1) {
            return new int[]{-1, -1};
        }
        return new int[]{left(arr,t),right(arr,t)};   
    }
    public static int left(int[] arr, int t) {
        if (arr == null || arr.length < 1) {
            return -1;
        }
        int ans = -1;
        int l = 0;
        int r = arr.length - 1;
        while (l <= r) {
            int m = l + ((r - l) >> 1);
            if (arr[m] == t) {
               ans = m;
               r = m - 1;
            } else if (arr[m] < t) {
                l = m +1;
            } else {
                // arr[m] > t
                r = m - 1;
            }
        }
        return ans;
    }
    public static int right(int[] arr, int t) {
        if (arr == null || arr.length < 1) {
            return -1;
        }
        int ans = -1;
        int l = 0;
        int r = arr.length - 1;
        while (l <= r) {
            int m = l + ((r - l) >> 1);
            if (arr[m] == t) {
               ans = m;
               l = m + 1;
            } else if (arr[m] < t) {
                l = m +1;
            } else {
                // arr[m] > t
                r = m - 1;
            }
        }
        return ans;
    }
}

时间复杂度 O(logN)。

局部最大值问题

思路

假设数组长度为N，首先判断0号位置的数和N-1位置的数是不是峰值位置。

0号位置只需要和1号位置比较，如果0号位置大，0号位置就是峰值位置，可以直接返回。

N-1号位置只需要和N-2号位置比较，如果N-1号位置大，N-1号位置就是峰值位置，可以直接返回。

如果0号位置和N-1在上轮比较中均是最小值，那么数组的样子必然是如下情况：

由上图可知，[0..1]区间内是增长趋势, [N-2...N-1]区间内是下降趋势。

那么峰值位置必在[1...N-2]之间出现。

此时可以通过二分来找峰值位置，先来到中点位置，假设为mid，如果中点位置的值比左右两边的值都大:

arr[mid] > arr[mid+1] && arr[mid] > arr[mid-1]

则mid位置即峰值位置，直接返回。

否则，有如下两种情况：

情况一：mid 位置的值比 mid - 1 位置的值小

趋势如下图：

则在[1...(mid-1)]区间内继续二分。

情况二：mid 位置的值比 mid + 1 位置的值小

趋势是：

则在[(mid+1)...(N-2)]区间内继续上述二分。

完整代码

public class LeetCode_0162_FindPeakElement {
    public static int findPeakElement(int[] nums) {
        if (nums.length == 1) {
            return 0;
        }
        int l = 0;
        int r = nums.length - 1;
        if (nums[l] > nums[l + 1]) {
            return l;
        }
        if (nums[r] > nums[r - 1]) {
            return r;
        }
        l = l + 1;
        r = r - 1;
        while (l <= r) {
            int mid = l + ((r - l) >> 1);
            if (nums[mid] > nums[mid + 1] && nums[mid] > nums[mid - 1]) {
                return mid;
            }
            if (nums[mid] < nums[mid + 1]) {
                l = mid + 1;
            } else if (nums[mid] < nums[mid - 1]) {
                r = mid - 1;
            }
        }
        return -1;
    }
}

时间复杂度O(logN)。

到此这篇关于详解Java中二分法的基本思路和实现的文章就介绍到这了,更多相关Java二分法内容请搜索编程网以前的文章或继续浏览下面的相关文章希望大家以后多多支持编程网！

您可能感兴趣的文档:

--结束END--

本文标题: 详解Java中二分法的基本思路和实现

本文链接: https://lsjlt.com/news/165945.html(转载时请注明来源链接)

有问题或投稿请发送至: 邮箱/279061341@qq.com QQ/279061341