扫码关注官方微信

扫码下载APP
返回顶部
首页 > 资讯 > 后端开发 > Python >Java实现链表数据结构的方法
  • 713

0
分享到

Java实现链表数据结构的方法

2024-04-02 19:04:59 713人浏览 安东尼

Python 官方文档：入门教程 => 点击学习

摘要

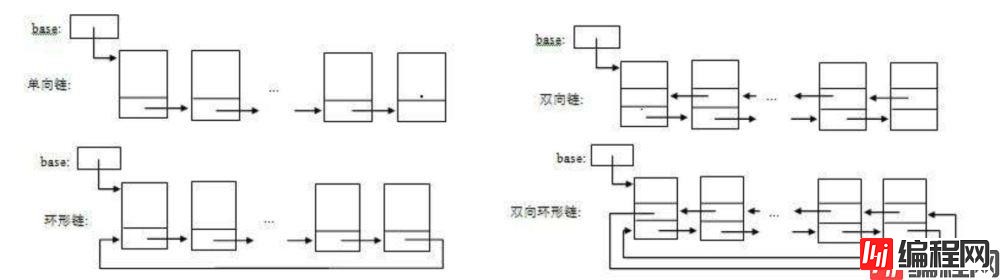
什么是链表？ 链表是一种物理存储单元上非连续、非顺序的存储结构，数据元素的逻辑顺序是通过链表中的指针连接次序实现的。每一个链表都包含多个节点，节点又包含两个部分，一个是数据域（储存节

什么是链表？

链表是一种物理存储单元上非连续、非顺序的存储结构，数据元素的逻辑顺序是通过链表中的指针连接次序实现的。
每一个链表都包含多个节点，节点又包含两个部分，一个是数据域（储存节点含有的信息），一个是引用域（储存下一个节点或者上一个节点的地址）。

链表的理解示意图:

在这里插入图片描述

链表的特点是什么？

获取数据麻烦，需要遍历查找，比数组慢
方便插入、删除

简单的链表的实现原理

创建一个节点类，其中节点类包含两个部分，第一个是数据域（你到时候要往节点里面储存的信息），第二个是引用域（相当于指针，单向链表有一个指针，指向下一个节点；双向链表有两个指针，分别指向下一个和上一个节点）

创建一个链表类，其中链表类包含三个属性：头结点、尾节点和大小，方法包含添加、删除、插入等等方法。 通用节点抽象类

package com.lineardatastructure.linked;


public abstract class LinkedAbs<T> implements Iterable<T> {
    //列表长度
    public int size = 0;
    //当前节点
    public node head;
    //尾节点
    public Node end;
    //节点
    protected class Node {
        Node previous = null;//上一个结点
        Node next = null;//下一个结点
        T data;//结点数据
        public Node(T data, Node next) {
            this.data = data;
            this.next = next;
        }
        public Node(Node next, Node previous) {
            this.next = next;
            this.previous = previous;
        }
        public Node(T data, Node next, Node previous) {
            this.next = next;
            this.previous = previous;
        }
        public Node(T data) {
            this.data = data;
        }
    }
    
    public Node isRinged(){
        if(head == null){
            return null;
        }
          Node slow = head;
        Node fast = head;
        while(fast.next != null && fast.next.next != null){
            slow = slow.next;
            fast = fast.next.next;
            if(fast == slow){
                return fast;
            }
        }
        return null;
    }
    // 获取链表头元素
    public T getFrom() {
        return head.data;
    }
    //获取链表结尾元素
    public T getEnd() {
        return end.data;
    }
    //获取链表中元素个数
    public int getSize() {
        return size;
    }
    
    public boolean isEmpty() {
        return size == 0;
    }
    
    public void stackDestroy() {
        head = null;
        size = 0;
        end=null;
    }
    //寻找单链表的中间结点：
    public  abstract T findMiddle();
    
    public abstract void reserveLink();
    
    public abstract T get(int index);
    
    public abstract void addFirst(T e);
    public abstract void addlast(T e);
    public abstract void add(T e);
    
    public abstract boolean remove(T obj);
    public abstract boolean remove(int index);
    public abstract boolean removeFirst();
    public abstract boolean removeLast();
}

实现单向链表

在这里插入图片描述


package com.lineardatastructure.linked;
import java.util.Iterator;

// 单向链表
public class OneWayLinked<T> extends LinkedAbs<T> {
    @Override
    public void reserveLink() {
        Node curNode = head;//头结点
        Node preNode = null;//前一个结点
        while(curNode != null){
            Node nextNode = curNode.next;//保留下一个结点
            curNode.next = preNode;//指针反转
            preNode = curNode;//前结点后移
            curNode = nextNode;//当前结点后移
        }
        head = preNode;
    }
    
    @Override
    public T findMiddle() {
        Node slowPoint = head;
        Node quickPoint = head;
        //quickPoint.next == null是链表结点个数为奇数时，快指针已经走到最后了
        //quickPoint.next.next == null是链表结点数为偶数时，快指针已经走到倒数第二个结点了
        //链表结点个数为奇数时,返回的是中间结点；链表结点个数为偶数时，返回的是中间两个结点中的前一个
        while (quickPoint.next != null && quickPoint.next.next != null) {
            slowPoint = slowPoint.next;
            quickPoint = quickPoint.next.next;
        }
        return slowPoint.data;
    }
    
    @Override
    public T get(int index) {
        if(size<0 || index>size){//待查询结点不存在
            return null;
        }
        if(index == 0){//查询头结点
            return head.data;
        }
        Node curNode =head;
        int i = 0;
        while (curNode != null) {
            if(i==index){//寻找到待查询结点
                return  curNode.data;
            }
            //当先结点和前结点同时向后移
            curNode = curNode.next;
            i++;
        }
        return null;
    }
    @Override
    public void addFirst(T e) {
    }
    @Override
    public void addlast(T e) {
    }
    
    @Override
    public void add(T data) {
        Node newNode = new Node(data);
        if (head == null) {
            head = newNode;
            end=head;//添加尾节点
            size++;
            return;
        }
        Node temp = end;
        temp.next = newNode;
        end=newNode;//修改尾节点
        size++;
    }
    
    @Override
    public boolean remove(T obj) {
        if (head.data.equals(obj)) {//删除头结点
            head = head.next;
            size=0;
            return true;
        }
        Node preNode = head;
        Node curNode = preNode.next;
        while (curNode != null) {
            if (curNode.data.equals(obj)) {//寻找到待删除结点
                preNode.next = curNode.next;//待删除结点的前结点指向待删除结点的后结点
                size--;
                return true;
            }
            //当先结点和前结点同时向后移
            preNode = preNode.next;
            curNode = curNode.next;
        }
        return  false;
    }
    @Override
    public boolean remove(int index) {
        if(size<0 || index>size){//待删除结点不存在
            return false;
        }
        if(index == 0){//删除头结点
            head = head.next;
            return true;
        }
        Node preNode = head;
        Node curNode =head.next;
        int i =1; //从第2个值开始
        while(preNode.next != null){
            if(i==index){//寻找到待删除结点
                preNode.next= curNode.next;//待删除结点的前结点指向待删除结点的后结点
                return true;
            }
            //当先结点和前结点同时向后移
            preNode=curNode;
            curNode = curNode.next;
            i++;
        }
        return false;
    }
    @Override
    public boolean removeFirst() {
        return false;
    }
    @Override
    public boolean removeLast() {
        return false;
    }
    @Override
    public Iterator<T> iterator() {
        return new Iterator<T>() {
            Node cursor = head;
            T data;
            @Override
            public boolean hasNext() {
                if (cursor != null) {
                    data = cursor.data;
                    cursor = cursor.next;
                    return true;
                }
                return false;
            }
            @Override
            public T next() {
                return data;
            }
            @Override
            public void remove() {
                OneWayLinked.this.remove(data);
            }
        };
    }
}

单向环形链表

它和单链表的区别在于结尾点的指针域不是指向null，而是指向头结点，形成首尾相连的环。这种首尾相连的单链表称为单向循环链表。循环链表可以从任意一个结点出发，访问到链表中的全部结点。

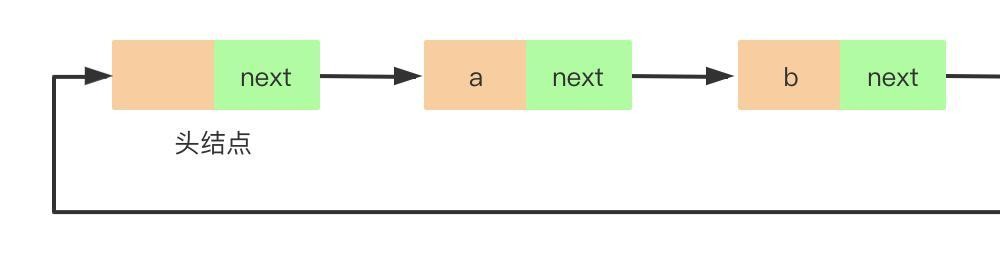
在这里插入图片描述


单向循环链表的查找、删除和修改操作与单链表一致(这里不在赘述，可参考前面的内容)，插入操作和单链表有所不同，单向循环链表需要维持环状结构。判断单链表为空的条件是head.next == null，而判断单向循环链表为空的条件为head.next == head。

package com.lineardatastructure.linked;
import java.util.Iterator;

// 单向循环链表
public class OneLoopWayLinked<T> extends LinkedAbs<T> {
    @Override
    public void reserveLink() {
        Object[] ts = new Object[size];
        int i = size - 1;
        for (T t : this) {
            ts[i] = t;
            i--;
        }
        Node node = head;
        node.data = (T) ts[0];
        for (int i1 = 1; i1 < ts.length; i1++) {
            Node node1 = new Node((T) ts[i1]);
            node.next = node1;
            node = node1;
            end= node1;
        }
        //调整位置
        end.next=head;
    }
    
    @Override
    public T findMiddle() {
        Node slowPoint = head;
        Node quickPoint = head;
        //quickPoint.next == null是链表结点个数为奇数时，快指针已经走到最后了
        //quickPoint.next.next == null是链表结点数为偶数时，快指针已经走到倒数第二个结点了
        //链表结点个数为奇数时,返回的是中间结点；链表结点个数为偶数时，返回的是中间两个结点中的前一个
        while (quickPoint.next != head && quickPoint.next.next != head) {
            slowPoint = slowPoint.next;
            quickPoint = quickPoint.next.next;
        }
        return slowPoint.data;
    }
    
    @Override
    public T get(int index) {
        if (size < 0 || index > size) {//待查询结点不存在
            return null;
        }
        if (index == 0) {//查询头结点
            return head.data;
        }
        Node curNode = head.next;
        int i = 1;
        while (curNode != head) {
            if (i == index) {//寻找到待查询结点
                return curNode.data;
            }
            //当先结点和前结点同时向后移
            curNode = curNode.next;
            i++;
        }
        return null;
    }
    @Override
    public void addFirst(T e) {
    }
    @Override
    public void addlast(T e) {
    }
    
    @Override
    public void add(T data) {
        Node newNode = new Node(data);
        if (head == null) {
            head = newNode;
            head.next = head; //环型
            end = head;//添加尾节点
            size++;
            return;
        }
        Node temp = end;
        //一直遍历到最后
        temp.next = newNode;
        newNode.next = head;//环型
        end = newNode;//修改尾节点
        size++;
    }
    
    @Override
    public boolean remove(T obj) {
        if (head.data.equals(obj)) {//删除头结点
            head = head.next;
            end.next=head;//调整环
            size--;
            return true;
        }
        Node preNode = head;
        Node curNode = preNode.next;
        while (curNode != head) {
            if (curNode.data.equals(obj)) {//寻找到待删除结点
                preNode.next = curNode.next;//待删除结点的前结点指向待删除结点的后结点
                size--;
                return true;
            }
            //当先结点和前结点同时向后移
            preNode = preNode.next;
            curNode = curNode.next;
        }
        return false;
    }
    @Override
    public boolean remove(int index) {
        if (size < 0 || index > size) {//待删除结点不存在
            return false;
        }
        if (index == 0) {//删除头结点
            head = head.next;
            end.next=head;//调整环
            size--;
            return true;
        }
        Node preNode = head;
        Node curNode = head.next;
        int i = 1; //从第2个值开始
        while (preNode.next != head) {
            if (i == index) {//寻找到待删除结点
                preNode.next = curNode.next;//待删除结点的前结点指向待删除结点的后结点
                return true;
            }
            //当先结点和前结点同时向后移
            preNode = curNode;
            curNode = curNode.next;
            i++;
        }
        size--;
        return false;
    }
    @Override
    public boolean removeFirst() {
        return false;
    }
    @Override
    public boolean removeLast() {
        return false;
    }
    @Override
    public Iterator<T> iterator() {
        return new Iterator<T>() {
            Node cursor = head;
            T data;
            @Override
            public boolean hasNext() {
                if (cursor != null&&cursor.next != head) {
                    data = cursor.data;
                    cursor = cursor.next;
                    return true;
                }
                if (cursor != null) {
                    data = cursor.data;
                    cursor = null;
                    return true;
                }
                return false;
            }
            @Override
            public T next() {
                return data;
            }
            @Override
            public void remove() {
                OneLoopWayLinked.this.remove(data);
            }
        };
    }
}

实现双向链表

在这里插入图片描述

package com.lineardatastructure.linked;
import java.util.Iterator;

public class BothwayLinked<T> extends LinkedAbs<T> {
    
    @Override
    public T get(int index) {
        if (size < 0 || index > size) {//待查询结点不存在
            return null;
        }
        if (index == 0) {//查询头结点
            return head.data;
        }
        Node curNode = head;
        int i = 0;
        while (curNode != null) {
            if (i == index) {//寻找到待查询结点
                return curNode.data;
            }
            //当先结点和前结点同时向后移
            curNode = curNode.next;
            i++;
        }
        return null;
    }
    @Override
    public void addFirst(T e) {
        Node next = head;
        Node previous = new Node(e);
        previous.next = next;
        next.previous = previous;
        head=previous;
        size++;
    }
    @Override
    public void addlast(T e) {
        Node newNode = new Node(e);
        if (head == null) {
            head = newNode;
            size++;
            end=head;//添加尾节点
            return;
        }
        Node temp = end;
        temp.next = newNode;
        newNode.previous = temp;
        end=newNode;//修改尾节点
        size++;
    }
    @Override
    public void add(T e) {
        addlast(e);
    }
    @Override
    public boolean remove(T obj) {
        if (removeHead()) {
            return true;
        }
        Node curNode = head;
        while (curNode != null) {
            //寻找到待删除结点
            if (curNode.data.equals(obj)) {
                //将删除的节点后节点,覆盖删除的节点,然后将父节点指向被删除元素的父节点
                Node previous = curNode.previous;
                Node next = curNode.next;
                if (next == null) {
                    //删除的是最后节点,那么就把他上一个节点的下一个节点删除
                    previous.next=null;
                } else if (previous==null) {
                    //删除的是头节点的话,那么就不管父节点了
                    head=head.next;
                    head.previous=null;
                } else {
                    next.previous = previous;
                    previous.next = next;
                }
                size--;
                return true;
            }
            //当先结点向后移
            curNode = curNode.next;
        }
        return false;
    }
    @Override
    public boolean remove(int index) {
        if (index<0 ||index >= size) {//待删除结点不存在
            return false;
        }
        if (removeHead()) {
            return true;
        }
        Node curNode = head;
        int i = 0;
        while (curNode != null) {
            if (i == index) {//寻找到待删除结点
                //将删除的节点后节点,覆盖删除的节点,然后将父节点指向被删除元素的父节点
                Node previous = curNode.previous;
                Node next = curNode.next;
                if (next == null) {
                    //删除的是最后节点,那么就把他上一个节点的下一个节点删除
                    previous.next=null;
                } else if (previous==null) {
                    //删除的是头节点的话,那么就不管父节点了
                    head=head.next;
                    head.previous=null;
                } else {
                    next.previous = previous;
                    previous.next = next;
                }
                size--;
                return true;
            }
            //当先结点向后移
            curNode = curNode.next;
            i++;
        }
        return false;
    }
    @Override
    public boolean removeFirst() {
        if (removeHead()) {
            return true;
        }
        Node node = head.next;
        node.previous = null;
        head = node;
        size--;
        return false;
    }
    @Override
    public boolean removeLast() {
        if (removeHead()) {
            return true;
        }
        //删除尾节点
        end.previous.next=null;
        size--;
        return true;
    }
    //如果只有一个元素那么就将头删除
    public boolean removeHead() {
        if (head.next==null) {
            head=null;
            return true ;
        }
        return  false;
    }
    @Override
    public void reserveLink() {
        Object[] ts = new Object[size];
        int i = size - 1;
        for (T t : this) {
            ts[i] = t;
            i--;
        }
        Node node = head;
        node.data = (T) ts[0];
        for (int i1 = 1; i1 < ts.length; i1++) {
            Node node1 = new Node((T) ts[i1]);
            node.next = node1;
            node1.previous = node;
            node = node1;
        }
    }
    
    @Override
    public T findMiddle() {
        Node slowPoint = head;
        Node quickPoint = head;
        //quickPoint.next == null是链表结点个数为奇数时，快指针已经走到最后了
        //quickPoint.next.next == null是链表结点数为偶数时，快指针已经走到倒数第二个结点了
        //链表结点个数为奇数时,返回的是中间结点；链表结点个数为偶数时，返回的是中间两个结点中的前一个
        while (quickPoint.next != null && quickPoint.next.next != null) {
            slowPoint = slowPoint.next;
            quickPoint = quickPoint.next.next;
        }
        return slowPoint.data;
    }
    @Override
    public Iterator<T> iterator() {
        return new Iterator<T>() {
            Node cursor = head;
            T data;
            @Override
            public boolean hasNext() {
                if (cursor != null) {
                    data = cursor.data;
                    cursor = cursor.next;
                    return true;
                }
                return false;
            }
            @Override
            public T next() {
                return data;
            }
            @Override
            public void remove() {
                BothwayLinked.this.remove(data);
            }
        };
    }
}

双向循环链表

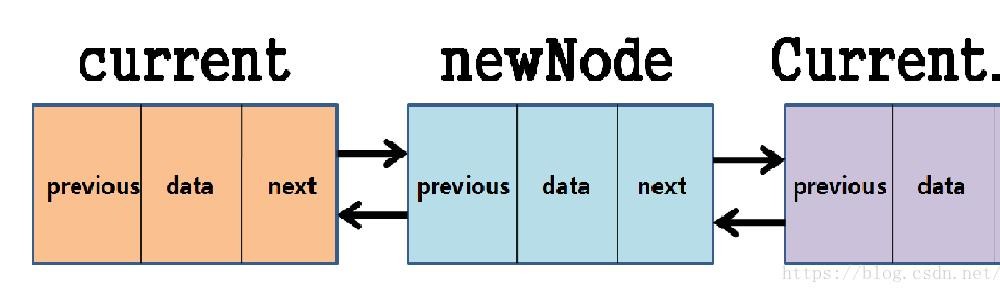
相比单链表，双向循环链表是一个更加复杂的结构。因为双向循环链表的节点不仅包含指向下一个节点的指针(next)，还包含指向前一个节点的指针(prev)。
在双向循环链表中，可见的不只有头指针head，还有尾节点end。这是和单链表的区别。
双向循环链表的头指针head的前一个节点指向end，尾节点end的后一个节点指向head。

在这里插入图片描述

注意: 双向循环链表,实现反查询特别容易只需要反过来遍历一遍就行

package com.lineardatastructure.linked;
import org.w3c.dom.Node;
import java.util.Iterator;

public class BothwayLoopLinked<T> extends LinkedAbs<T> {
    @Override
    public void reserveLink() {
        Object[] ts = new Object[size];
        int i = size - 1;
        for (T t : this) {
            ts[i] = t;
            i--;
        }
        Node node = head;
        node.data = (T) ts[0];
        for (int i1 = 1; i1 < ts.length; i1++) {
            Node node1 = new Node((T) ts[i1]);
            node.next = node1;
            node1.previous = node;
            node = node1;
            end= node1;
        }
        //调整位置
        head.previous=end;
        end.next=head;
    }
    
    @Override
    public T findMiddle() {
        Node slowPoint = head;
        Node quickPoint = head;
        //quickPoint.next == null是链表结点个数为奇数时，快指针已经走到最后了
        //quickPoint.next.next == null是链表结点数为偶数时，快指针已经走到倒数第二个结点了
        //链表结点个数为奇数时,返回的是中间结点；链表结点个数为偶数时，返回的是中间两个结点中的前一个
        while (quickPoint.next != head && quickPoint.next.next != head) {
            slowPoint = slowPoint.next;
            quickPoint = quickPoint.next.next;
        }
        return slowPoint.data;
    }
    
    @Override
    public T get(int index) {
        if (size < 0 || index > size) {//待查询结点不存在
            return null;
        }
        if (index == 0) {//查询头结点
            return head.data;
        }
        Node curNode = head.next;
        int i = 1;
        while ( curNode!= head) {
            if (i == index) {//寻找到待查询结点
                return curNode.data;
            }
            //当先结点和前结点同时向后移
            curNode = curNode.next;
            i++;
        }
        return null;
    }
    @Override
    public void addFirst(T e) {
        Node next = head;
        Node previous = new Node(e);
        previous.previous = head.previous;
        previous.next = next;
        next.previous = previous;
        head = previous;
        end.next=previous;//修改尾节点的指向
        size++;
    }
    @Override
    public void addlast(T e) {
        Node newNode = new Node(e);
        if (head == null) {
            head = newNode;
            head.previous=head;//环型
            head.next=head; //环型
            end=head;//添加尾节点
            size++;
            return;
        }
        Node temp = end;
        temp.next = newNode;
        newNode.previous = temp;
        newNode.next = head;//给为节点添加头节点(环型)
        end=newNode;//修改尾节点
        size++;
    }
    @Override
    public void add(T e) {
        addlast(e);
    }
    @Override
    public boolean remove(T obj) {
        if (removeHead()) {
            return true;
        }
        //头部删除需要特殊处理
        if (obj == head.data) {
            Node previous = head.previous;
            head = head.next;
            head.previous = previous;
            end.next=head;
            size--;
            return true;
        }
        Node curNode = head.next;
        while (curNode != head) {
            //寻找到待删除结点
            if (curNode.data.equals(obj)) {
                //将删除的节点后节点,覆盖删除的节点,然后将父节点指向被删除元素的父节点
                Node previous = curNode.previous;
                Node next = curNode.next;
                if (next == null) {
                    //删除的是最后节点,那么就把他上一个节点的下一个节点删除
                    previous.next = null;
                } else {
                    next.previous = previous;
                    previous.next = next;
                }
                size--;
                return true;
            }
            //当先结点向后移
            curNode = curNode.next;
        }
        return false;
    }
    @Override
    public boolean remove(int index) {
        if (removeHead()) {
            return true;
        }
        if (size < 0 || index >= size) {//待删除结点不存在
            return false;
        }
        //头部删除需要特殊处理
        if (index==0) {
            Node previous = head.previous;
            head = head.next;
            head.previous = previous;
            size--;
            return true;
        }
        Node curNode = head.next;
        int i = 1;
        while (curNode != null) {
            if (i == index) {//寻找到待删除结点
                //将删除的节点后节点,覆盖删除的节点,然后将父节点指向被删除元素的父节点
                Node previous = curNode.previous;
                Node next = curNode.next;
                if (next == null) {
                    //删除的是最后节点,那么就把他上一个节点的下一个节点给替换成头节点
                    previous.next = head;
                } else {
                    next.previous = previous;
                    previous.next = next;
                }
                size--;
                return true;
            }
            //当先结点向后移
            curNode = curNode.next;
            i++;
        }
        return false;
    }
    @Override
    public boolean removeFirst() {
        head = head.next;
        head.previous = end; //环绕
        end.next=head; //环绕
        size--;
        return false;
    }
    @Override
    public boolean removeLast() {
        //将删除结尾节点
        end.previous.next=head;
        size--;
        return true;
    }
    //如果只有一个元素那么就将头删除
    public boolean removeHead() {
        if (head.next==null) {
            head=null;
            return true ;
        }
        return  false;
    }
    @Override
    public Iterator<T> iterator() {
        return new Iterator<T>() {
            Node cursor = head;
            T data;
            @Override
            public boolean hasNext() {
                if (cursor != null&&cursor.next != head) {
                    data = cursor.data;
                    cursor = cursor.next;
                    return true;
                }
                if (cursor != null) {
                    data = cursor.data;
                    cursor = null;
                    return true;
                }
                return false;
            }
            @Override
            public T next() {
                return data;
            }
            @Override
            public void remove() {
                BothwayLoopLinked.this.remove(data);
            }
        };
    }
}

到此这篇关于Java实现链表数据结构的文章就介绍到这了,更多相关Java链表数据结构内容请搜索编程网以前的文章或继续浏览下面的相关文章希望大家以后多多支持编程网！

您可能感兴趣的文档:

--结束END--

本文标题: Java实现链表数据结构的方法

本文链接: https://lsjlt.com/news/162404.html(转载时请注明来源链接)

有问题或投稿请发送至: 邮箱/279061341@qq.com    QQ/279061341

猜你喜欢
  • Java实现链表数据结构的方法
    什么是链表？ 链表是一种物理存储单元上非连续、非顺序的存储结构，数据元素的逻辑顺序是通过链表中的指针连接次序实现的。每一个链表都包含多个节点，节点又包含两个部分，一个是数据域（储存节...
    99+
    2024-04-02
  • java数据结构中单链表与双向链表的实现方法
    这篇文章主要介绍“java数据结构中单链表与双向链表的实现方法”，在日常操作中，相信很多人在java数据结构中单链表与双向链表的实现方法问题上存在疑惑，小编查阅了各式资料，整理出简单好用的操作方法，希望对大家解答”java数据结构中单链表与...
    99+
    2023-06-20
  • 数据结构——链表(java)
    文章目录 链表1. 基本介绍1.1 定义1.2 链表分类3.不带头非循环单链表CURD4.不带头非循环双向链表CURD 链表 1. 基本介绍 1.1 定义 链表是一种物理存储结构...
    99+
    2023-10-02
    数据结构 链表 java
  • Java数据结构之双向链表的实现
    目录1 双向链表1.1 双向链表介绍1.2 双向链表实现思路2 双向链表实现完整代码2.1 节点类 Student.java2.2 双向链表实现类 StudentDoubleLink...
    99+
    2022-11-13
    Java 数据结构 双向链表 Java 双向链表
  • 数据结构（Java实现）LinkedList与链表（上）
    链表 逻辑结构 无头单向非循环链表：结构简单，一般不会单独用来存数据。实际中更多是作为其他数据结构的子结构，如哈希桶、图的邻接表等等。 无头双向链表：在Java的集合框架库中LinkedList底层实现就是无头双向循环链表。 ...
    99+
    2023-08-30
    数据结构 java 链表
  • Java数据结构之双端链表原理与实现方法
    本文实例讲述了Java数据结构之双端链表原理与实现方法。分享给大家供大家参考，具体如下：一、概述：什么时双端链表：链表中保持这对最后一个连点引用的链表从头部插入要对链表进行判断，如果为空则设置尾节点为新添加的节点从尾部进行插入如果链表为空，...
    99+
    2023-05-30
    java 数据结构 双端链表
  • JAVA版的数据结构——链表
    目录 1.单向不带头链表 1.1 链表的概念及结构 1.2 代码部分 1.3 完整的全部代码 2. 双向不带头链表 2.1 代码部分 2.2 完整的代码 3. MySingleList与MyLinkedList代码上的区别 4. Link...
    99+
    2023-09-12
    java 数据结构 链表
  • Java数据结构之LinkedList从链表到实现
    目录1.ArrayList的缺陷2.LinkedListLinkedList概念LinkedList的使用3.链表的概念及结构4.ArrayList和LinkedList的区别1.A...
    99+
    2023-05-18
    Java LinkedList Java 链表
  • java数据结构实现双向链表功能
    双向链表实现 双向链表也叫双链表，是链表的一种，它的每个数据结点中都有两个指针，分别指向直接后继和直接前驱。所以，从双向链表中的任意一个结点开始，都可以很方便地访问它的前驱结点和后继...
    99+
    2024-04-02
  • Java数据结构之实现哈希表的分离链接法
    哈希表的分离链接法 原理 Hash Table可以看作是一种特殊的数组。他的原理基本上跟数组相同，给他一个数据，经过自己设置的哈希函数变换得到一个位置，并在这个位置当中放置该数据。哦...
    99+
    2024-04-02
  • Java数据结构中实现哈希表的分离链接法
    这篇文章主要介绍“Java数据结构中实现哈希表的分离链接法”，在日常操作中，相信很多人在Java数据结构中实现哈希表的分离链接法问题上存在疑惑，小编查阅了各式资料，整理出简单好用的操作方法，希望对大家解答”Java数据结构中实现哈希表的分离...
    99+
    2023-06-20
  • Java链表数据结构及使用方法实例分析
    本篇内容主要讲解“Java链表数据结构及使用方法实例分析”，感兴趣的朋友不妨来看看。本文介绍的方法操作简单快捷，实用性强。下面就让小编来带大家学习“Java链表数据结构及使用方法实例分析”吧!认识链表结构单向链表单链表在内存中的表示：可以看...
    99+
    2023-07-02
  • 【一起学数据结构与算法】Java实现双链表
    目录 一、双链表的概念二、双链表一些方法的实现2.1 双链表的属性2.2 打印双链表2.3 得到双链表的长度2.4 查找是否包含关键字key是否在双链表中2.5 头插法2.6 尾插法2.7 任...
    99+
    2023-09-04
    java 链表 数据结构
  • 关于 Java 的数据结构链表
    目录数据结构关于 Java 的链表1. 删除链表中等于给定值 val 的所有节点2. 反转一个单链表3. 给定一个带有头结点 head 的非空单链表4. 输入一个链表，输出该链表中倒...
    99+
    2024-04-02
  • Java数据结构之链表实现（单向、双向链表及链表反转）
    前言 之前学习的顺序表查询非常快，时间复杂度为O(1)，但是增删改效率非常低，因为每一次增删改都会元素的移动。可以使用另一种存储方式-链式存储结构。 链表是一种物理存储单元上非连续、...
    99+
    2024-04-02
  • Java数据结构之双向链表如何实现
    这篇文章主要讲解了“Java数据结构之双向链表如何实现”，文中的讲解内容简单清晰，易于学习与理解，下面请大家跟着小编的思路慢慢深入，一起来研究和学习“Java数据结构之双向链表如何实现”吧！双向链表（Doubly linked list）什...
    99+
    2023-06-30
  • Java数据结构之链表的概念及结构
    目录1、链表的概念2、结点3、链表的使用场景4、链表分类和常用结构5、与顺序表的比较1、链表的概念 概念：链表是一种物理存储结构上非连续、非顺序的存储结构，数据元素的逻辑顺序是通过链...
    99+
    2023-05-14
    Java 数据结构链表概念结构 数据结构链表概念 数据结构链表结构
  • C++数据结构之单链表的实现
    目录一、单链表的定义二、单链表的基本操作的实现1.初始化2.取值3.查找4.插入5.删除三、完整代码四、测试一下代码一、单链表的定义 线性表的链式存储又称为单链表，它是指通过一组任意...
    99+
    2024-04-02
  • 数据结构：链表（Python语言实现）
    链表分为单链表、双链表、循环单链表和循环双链表。 本文以单链表为例，用python创建一个单链表数据结构，同时定义链表节点的增加、删除、查询和打印操作。 一、创建节点类 创建一个名为Node的节点类，节点类里面包含2个属性和1个方法。...
    99+
    2023-09-24
    链表 数据结构 python 算法 Powered by 金山文档
  • 用Python实现数据结构之链表
    链表与栈，队列不一样，它是由一个个节点构成的，每个节点存储着本身的一些信息，也存储着其他一个或多个节点的引用，可以从一个节点找到其他的节点，节点与节点之间就像是有链连在一起一样，这种数据结构就叫做链表 单向链表是链表的最简单形式，链表...
    99+
    2023-01-30
    数据结构 链表 Python
软考高级职称资格查询
热门wiki
近期文章
推荐阅读
热门问答
热门标签
编程网，编程工程师的家园，是目前国内优秀的开源技术社区之一，形成了由开源软件库、代码分享、资讯、协作翻译、讨论区和博客等几大频道内容，为IT开发者提供了一个发现、使用、并交流开源技术的平台。

  • 官方手机版

  • 微信公众号

  • 商务合作