Python 官方文档:入门教程 => 点击学习
目录1. 普通搜索2. 顺序搜索1.1 无序下的顺序查找1.2 有序下的顺序查找2.二分查找3.散列查找3.1 几种散列函数3.2 处理散列表冲突3.3 散列表的实现(加1重复)4.
往期学习:
python数据类型: Python数据结构:数据类型.
python的输入输出: python数据结构之输入输出及控制和异常.
python面向对象: python数据结构面向对象.
python算法分析: python数据结构之算法分析.
python栈、队列和双端队列:python数据结构栈、队列和双端队列.
python递归: python数据结构之递归.
上一期讲的递归,对于初学者其实是不太友好的,递归需要自己多去接触,自己多画画图,这样可以加强理解递归的过程,本期我们要讲的内容是搜索,也可以叫查找。我将讲解几种最为普遍的查找算法。
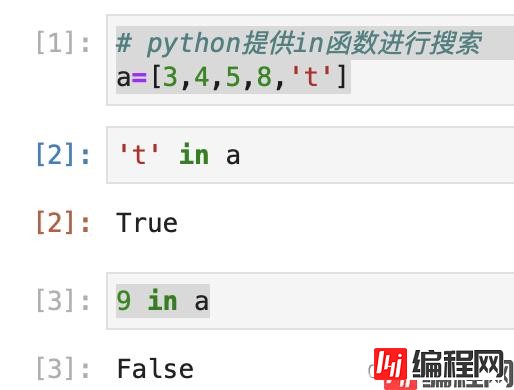
搜索是指从元素集合中找到某个特定元素的算法过程。搜索过程通常返回 True 或 False, 分别表示元素是否存在。python中提供了 in 方法可以判断元素是否存在列表中:
# python提供in函数进行搜索
a=[3,4,5,8,'t']
't' in a
9 in a
结果如下:
顺序搜索故名思义:从列表中的第一个元素开始,沿着默认的顺序逐个查看, 直到找到目标元素或者查完列表。如果查完列表后仍没有找到目标元素,则说明目标元素不在列表中。
顺序搜索过程:

无序下的顺序搜索很有特点,列表无序,只好一个一个去比较,寻找元素。
#顺序查找
def sequentialsearch(testlist,item):
pos=0
found=False
while pos<len(testlist) and not found:
if testlist[pos]==item:
found=True
else:
pos=pos+1
return found
结果如下:
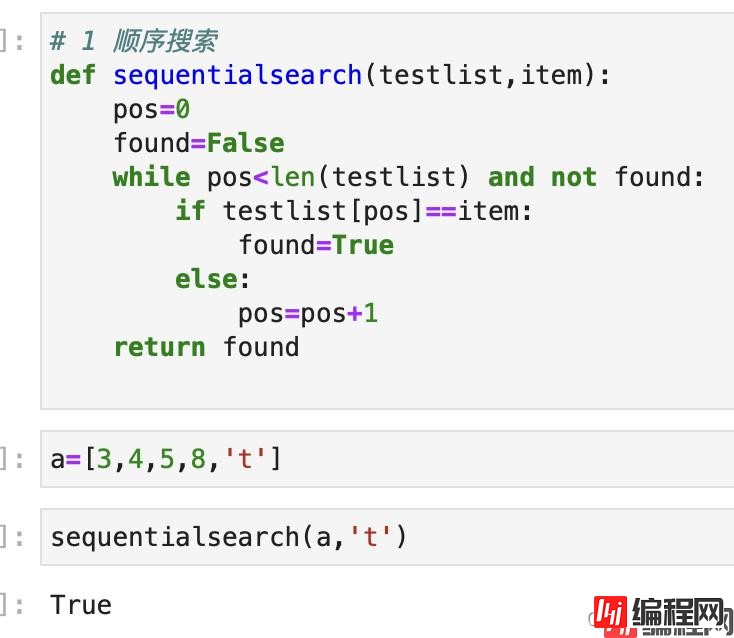
分析一下这种顺序查找,这种查找方式,最好的方式就寻找一次就成功了,最坏的情况的需要查找n次,于是时间复杂度是O(n)
有序下的顺序查找就是所查找的列表是有序的,
# 有序下的顺序搜索
def ordersearch(testlist,item):
pos=0
found=False
stop=False
while pos<len(testlist) and not found and not stop:
if testlist[pos]==item:
found=True
else:
if testlist[pos]>item:
stop=True
else:
pos=pos+1
return found
结果如下:
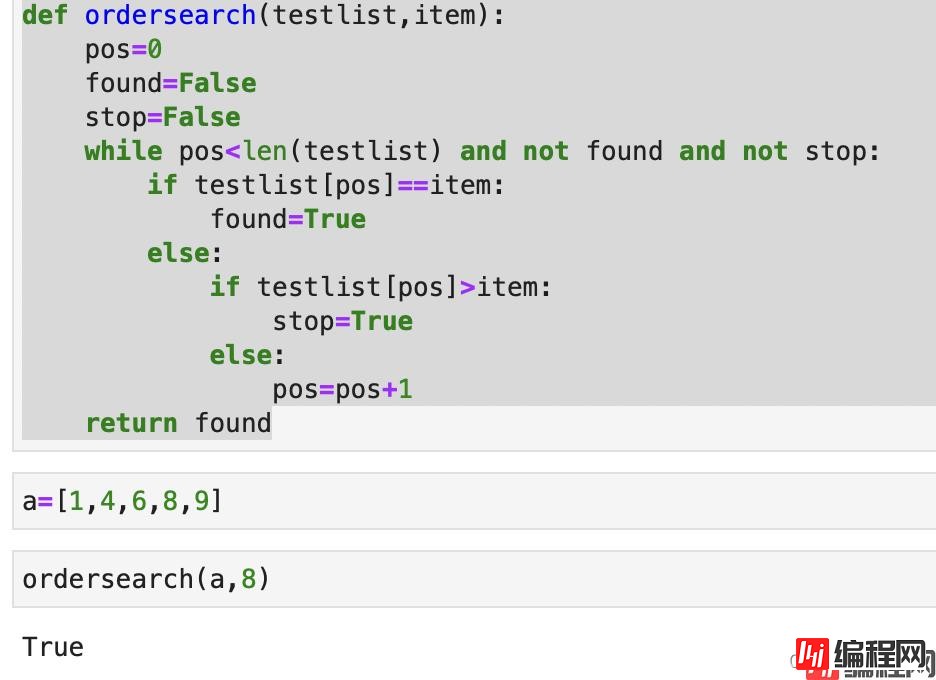
分析一下这种搜索方法,正常情况下来说,最好情况下,搜索1次就能成功,最差情况只需要n/2次即可搜索完成,但时间复杂度依旧是O(n),只有当列表中不存在目标元素时,有序排列的元素才会提高顺序搜索的效率。
二分查找:是利用列表有序的这个原理,从中间的元素着手。如果这个元素就是目标元素,那就立即停止搜索;如果不是,则可以利用列表有序的特性,排除一半的元素。如果目标元素比中间的元素大,就可以直接排除列表的左半部分和中间的元素。这是因为,如果列表包含目标元素,它必定位于右半部分。
在有序整数列表中进行二分搜索:
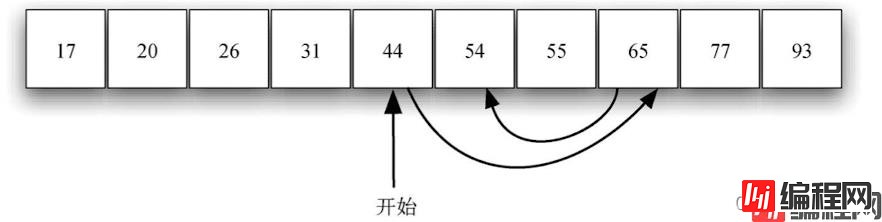
二分查找实现方式:
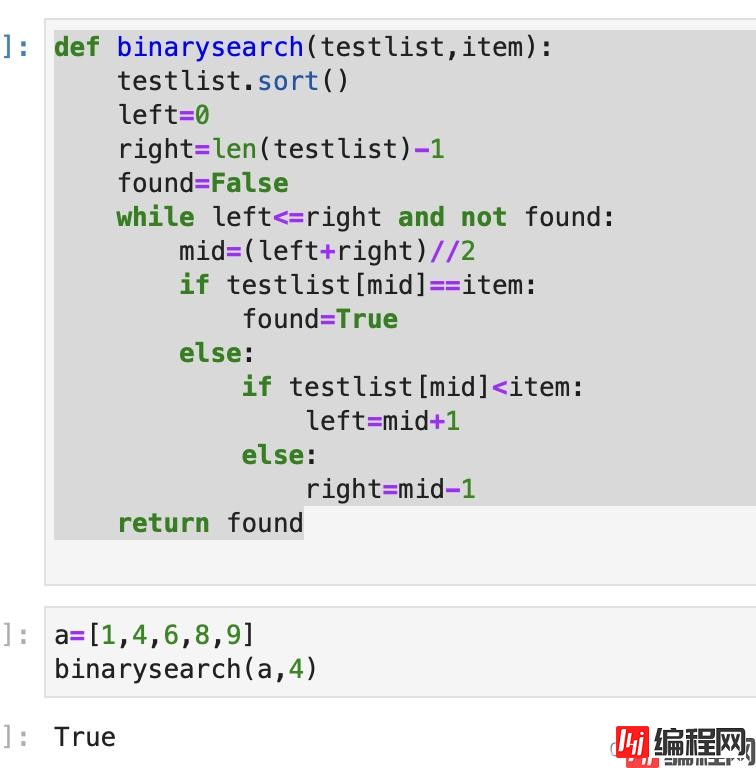
def binarysearch(testlist,item):
testlist.sort()#排序
left=0#左指针
right=len(testlist)-1#右指针
found=False
while left<=right and not found:
mid=(left+right)//2#取中间值
if testlist[mid]==item:
found=True
else:
if testlist[mid]<item:
left=mid+1
else:
right=mid-1
return found
看看效果:
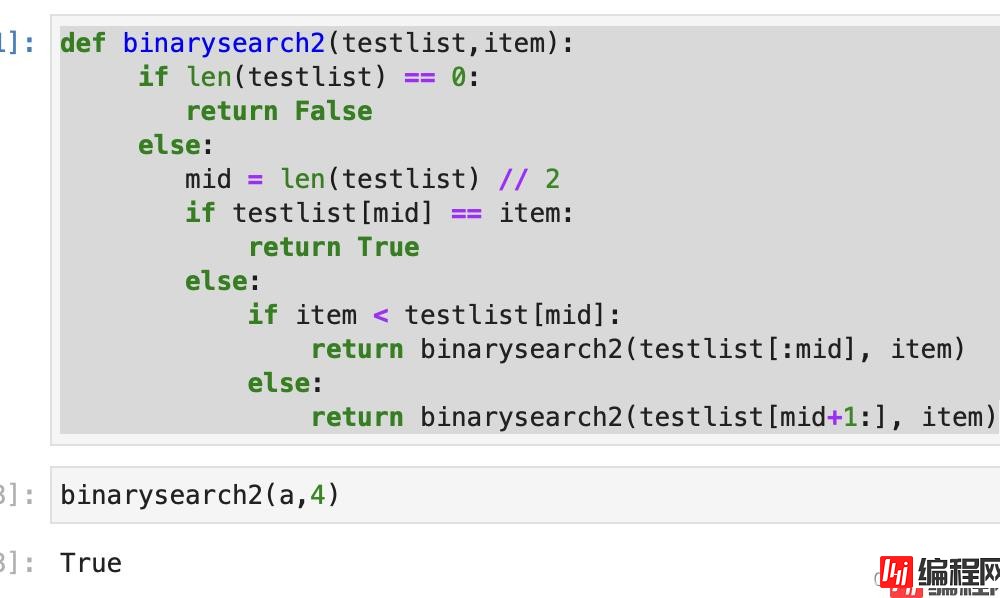
二分查找递归实现:
def binarysearch2(testlist,item):
if len(testlist) == 0:
return False
else:
mid = len(testlist) // 2
if testlist[mid] == item:
return True
else:
if item < testlist[mid]:
return binarysearch2(testlist[:mid], item)
else:
return binarysearch2(testlist[mid+1:], item)
看看效果:
总结一下二分查找:在进行二分搜索时,每一次比较都将待考虑的元素减半,。那么,要检查完整个列表,二分搜索算法最多要比较多少次呢?假设列表共有 n 个元素,第一次比较后剩下n 个元素,第 2 次比较2后剩下n /4个元素,接下来是n/8 ,然后是n/16 ,依此类推。列表能拆分多少次?
二分搜索算法的表格分:


散列查找:通过散列构建一个时间复杂度为 O(1)的数据结构。我们平常听的最多哈希表就是散列的一种方式。
散列表:散列表是元素集合,其中的元素以一种便于查找的方式存储。散列表中的每个位置通常被称 为槽,其中可以存储一个元素。槽用一个从 0 开始的整数标记,例如 0 号槽、1 号槽、2 号槽, 等等。初始情形下,散列表中没有元素,每个槽都是空的。可以用列表来实现散列表,并将每个元素都初始化为 Python 中的特殊值 None。下图展示了大小 m 为 11 的散列表。也就是说,表中有 m 个槽,编号从 0 到 10。
有11 个槽的散列表:
:

散列函数:将散列表中的元素与其所属位置对应起来。对散列表中的任一元素,散列函数返回 一个介于 0 和 m – 1 之间的整数。假设有一个由整数元素 54、26、93、17、77 和 31 构成的集 合。首先来看第一个散列函数,它有时被称作“取余函数”,即用一个元素除以表的大小,并将 得到的余数作为散列值(h(item) = item%11)。下图给出了所有示例元素的散列值。取余函数是一个很常见的散列函数,这是因为结果必须在槽编号范围内。
使用余数作为散列值:

计算出散列值后,就可以将每个元素插入到相应的位置,如图 5-5 所示。注意,在 11 个槽 中,有 6 个被占用了。占用率被称作载荷因子,记作λ \lambdaλ,定义如下:

有 6 个元素的散列表:

给定一个元素集合,能将每个元素映射到不同的槽,这种散列函数称作完美散列函数。如果元素已知,并且集合不变,那么构建完美散列函数是可能的。不幸的是,给定任意一个元素集合,没有系统化方法来保证散列函数是完美的。所幸,不完美的散列函数也能有不错的性能。
完美的散列表,一个元素只对应着一个卡槽,可是如果当2个元素被分配到一个卡槽时,必须通过一种系统化方法在散列表中安置第二个元素。这个过程被称为处理冲突。
开发定址法:在散列表中找到另一个空槽,用于放置引起冲突的元素。简单的做法是从起初的散列值开始,顺序遍历散列表,直到找到一个空槽。注意,为了遍历散列表,可能需要往回检查第一个槽。(例如:将(54, 26, 93, 17, 77, 31, 44, 55, 20)放入卡槽中。)
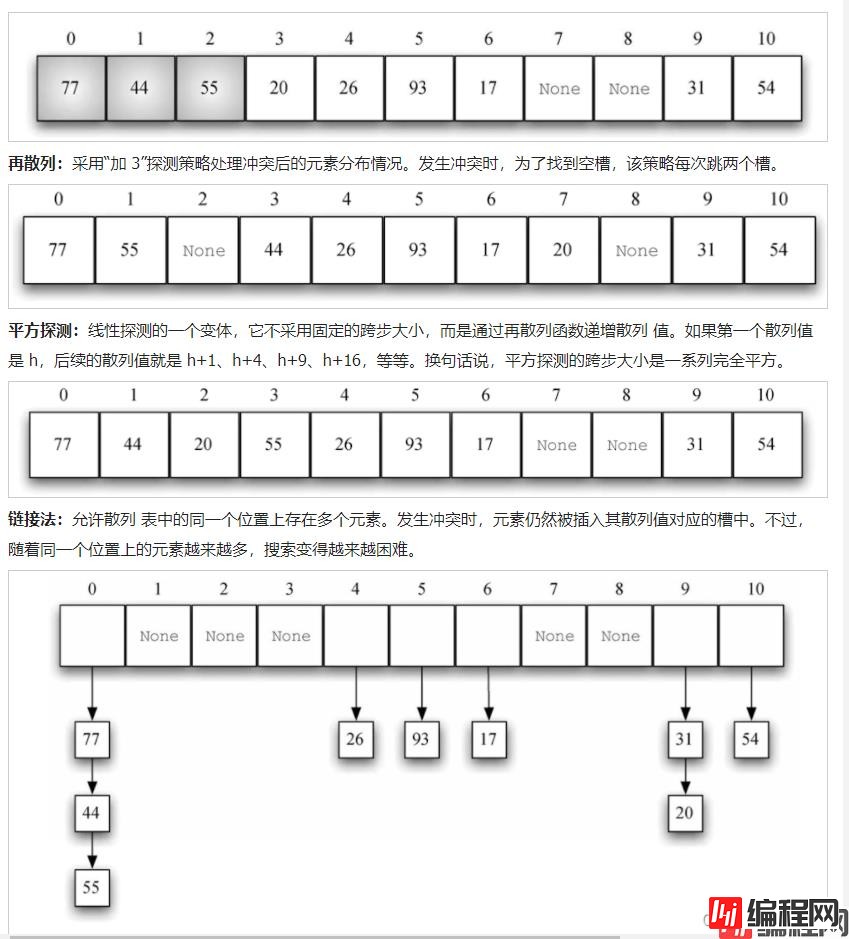
哈希散列的实现:
#哈希表
class HashTable:
def __init__(self):
self.size = 11
self.slots = [None] * self.size
self.data = [None] * self.size
def put(self, key, data):
hashvalue = self.hashfunction(key, len(self.slots))
if self.slots[hashvalue] == None:
self.slots[hashvalue] = key
self.data[hashvalue] = data
else:
if self.slots[hashvalue] == key:
self.data[hashvalue] = data #替换
else:
nextslot = self.rehash(hashvalue, len(self.slots))
while self.slots[nextslot] != None and self.slots[nextslot] != key:
nextslot = self.rehash(nextslot, len(self.slots))
if self.slots[nextslot] == None:
self.slots[nextslot] = key
self.data[nextslot] = data
else:
self.data[nextslot] = data #替换
def hashfunction(self, key, size):
return key%size
def rehash(self, oldhash, size):
return (oldhash + 1)%size
#get函数
def get(self, key):
startslot = self.hashfunction(key, len(self.slots))
data = None
stop = False
found = False
position = startslot
while self.slots[position] != None and not found and not stop:
if self.slots[position] == key:
found = True
data = self.data[position]
else:
position=self.rehash(position, len(self.slots))
if position == startslot:
stop = True
return data
def __getitem__(self, key):
return self.get(key)
def __setitem__(self, key, data):
self.put(key, data)
结果如下:
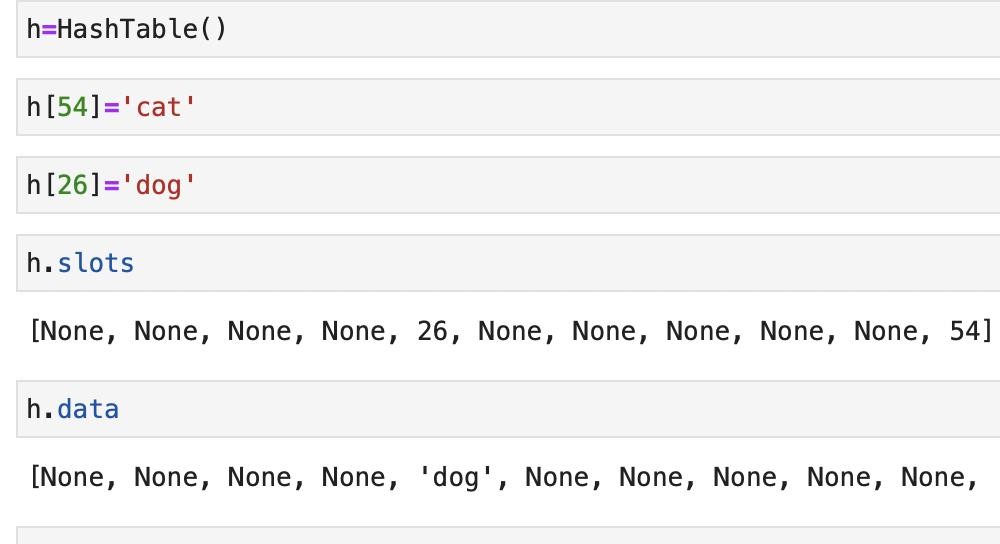
我们分析一下散列查找:在最好情况下,散列搜索算法的时间复杂度是 O(1),即常数阶。但可能发生冲突,所以比较次数通常不会这么简单。
到此这篇关于python数据结构之搜索讲解的文章就介绍到这了,更多相关python搜索讲解内容请搜索编程网以前的文章或继续浏览下面的相关文章希望大家以后多多支持编程网!
--结束END--
本文标题: python数据结构之搜索讲解
本文链接: https://lsjlt.com/news/160562.html(转载时请注明来源链接)
有问题或投稿请发送至: 邮箱/279061341@qq.com QQ/279061341
2024-03-01
2024-03-01
2024-03-01
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
回答
回答
回答
回答
回答
回答
回答
回答
回答
回答
0