Python 官方文档:入门教程 => 点击学习
目录1、如何认识可视化?2、StatsModels 绘图工具包 (Graphics)3、Matplotlib 绘图工具包4、Seaborn 绘图工具包5、多元回归案例分析(Stats
需要指出的是,虽然不同绘图工具包的功能、效果会有差异,但在常用功能上相差并不是很大。与选择哪种绘图工具包相比,更重要的是针对不同的问题,需要思考选择什么方式、何种图形去展示分析过程和结果。换句话说,可视化只是手段和形式,手段要为目的服务,形式要为内容服务,这个关系一定不能颠倒了。
因此,可视化是伴随着分析问题、解决问题的过程而进行思考、设计和实现的,而且还会影响问题的分析和解决过程:
回归分析是基于数据的建模,在导入数据后首先要进行数据探索,对给出的或收集的数据有个大概的了解,主要包括数据质量探索和数据特征分析。数据准备中的异常值分析,往往就需要用到箱形图(Boxplot)。对于数据特征的分析,经常使用频率分布图或频率分布直方图(Hist),饼图(Pie)。
对于问题中变量之间的关系,有些可以通过定性分析来确定或猜想,需要进一步的验证,有些复杂关系难以由分析得到,则要通过对数据进行初步的相关分析来寻找线索。在分析问题、尝试求解的过程中,虽然可以得到各种统计量、特征值,但可视化图形能提供更快捷、直观、丰富的信息,对于发现规律、产生灵感很有帮助。
在解决问题的过程中,也经常会希望尽快获得初步的结果、总体的评价,以便确认解决问题的思路和方法是否正确。这些情况下,我们更关心的往往是绘图的便捷性,图形的表现效果反而是次要的。
问题解决之后需要对结果进行呈现或发表,这时则需要结合表达的需要,特别是表达的逻辑框架,设计可视化的方案,选择适当的图形种类和形式,准备图形数据。在此基础上,才谈得上选择何种绘图工具包,如何呈现更好的表现效果。
Statsmodels 本身支持绘图功能(Graphics),包括拟合图(Fit Plots)、箱线图(Box Plots)、相关图(Correlation Plots)、函数图(Functional Plots)、回归图(Regression Plots)和时间序列图(Time Series Plots)。
Statsmodels 内置绘图功能 Graphics 的使用似乎并不流行,网络上的介绍也不多。分析其原因,一是 Graphics 做的并不太好用,文档和例程不友好,二是学习成本高:能用通用的可视化包实现的功能,何必还要花时间去学习一个专用的 Graphics?
下面是 Statsmodels 官方文档的例程,最简单的单变量线性回归问题,绘制样本数据散点图和拟合直线图。Graphics 提供了将拟合与绘图合二为一的函数 qqline(),但是为了绘制出样本数据则要调用 Matplotlib 的 matplotlib.pyplot.scatter(),所以…
import statsmodels.api as sm
import matplotlib.pyplot as plt
from statsmodels.graphics.Gofplots import qqline
foodexp = sm.datasets.engel.load(as_pandas=False)
x = foodexp.exog
y = foodexp.endog
ax = plt.subplot(111)
plt.scatter(x, y)
qqline(ax, "r", x, y)
plt.show()
# = 关注 Youcans,分享原创系列 https://blog.csdn.net/youcans =


下图看起来有点象 Seaborn中的 relplot,但把官方文档研究了半天也没搞明白,只好直接分析例程和数据,最后的结论是:基本没啥用。
这大概就是更多用户直接选择 Python 的可视化工具包进行绘图的原因吧。最常用的当属 Matplotlib 无疑,而在统计回归分析中 Seaborn 绘图工具包则更好用更炫酷。
Matplotlib 绘图包就不用介绍了。Matplotlib 用于 Statsmodels 可视化,最大的优势在于Matplotlib 谁都会用,实现统计回归的基本图形的也很简单。如果需要复杂的图形,炫酷的效果,虽然 Matplotlib 原理上也能实现,但往往需要比较繁琐的数据准备,并不常用的函数和参数设置。既然学习成本高,出错概率大,就没必要非 Matplotlib 不可了。
Matplotlib 在统计回归问题中经常用到的是折线图、散点图、箱线图和直方图。这也是 Matplotlib 最常用的绘图形式,本系列文中也有相关例程,本文不再具体介绍相关函数的用法。
例如,在本系列《Python学习笔记-StatsModels 统计回归(2)线性回归》的例程和附图,不仅显示了原始检测数据、理论模型数据、拟合模型数据,而且给出了置信区间的上下限,看起来还是比较“高级”的。但是,如果把置信区间的边界线隐藏起来,图形马上就显得不那么“高级”,比较“平常”了——这就是选择什么方式、何种图形进行展示的区别。


由此所反映的问题,还是表达的逻辑和数据的准备:要表达什么内容,为什么要表达这个内容,有没有相应的数据?问题的关键并不是什么工具包或什么函数,更不是什么颜色什么线性,而是有没有置信区间上下限的数据。
如果需要复杂的图形,炫酷的效果,虽然 Matplotlib 原理上也能实现,但往往需要比较繁琐的数据准备,使用并不常用的函数和参数设置。学习成本高,出错概率大,就没必要非 Matplotlib 不可了。
Seaborn 是在 Matplotlib 上构建的,支持 Scipy 和 Statamodels 的统计模型可视化,可以实现:
Seaborn 绘图工具包以数据可视化为中心来挖掘与理解数据,本身就带有一定的统计回归功能,而且简单好用,特别适合进行定性分析、初步评价。
下图给出了几种常用的 Seaborn 图形,分别是带拟合线的直方图(distplot)、箱线图(boxplot)、散点图(scatterplot)和回归图(regplot),后文给出了对应的程序。
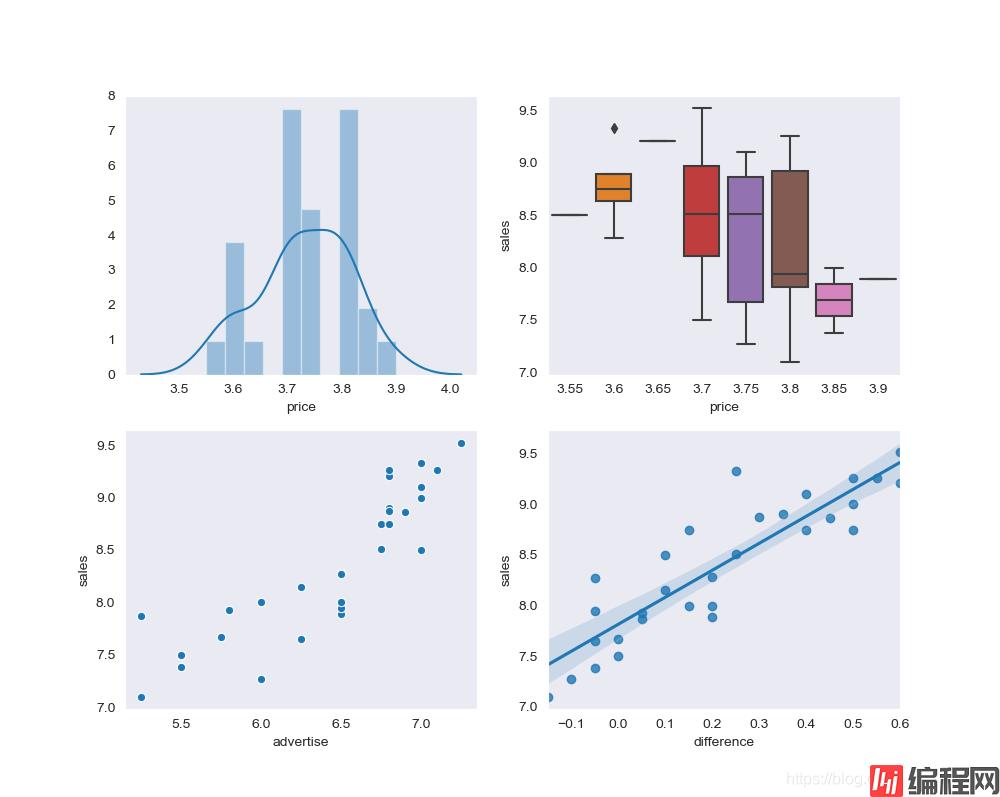
实际上,这些图形用 StatsModels Graphics、Matplotlib 也可以绘制,估计任何绘图包都可以实现。那么,为什么还要推荐 Seaborn 工具包,把这些图归入 Seaborn 的实例呢?我们来看看实现的例程就明白了:简单,便捷,舒服。不需要数据准备和变换处理,直接调用变量数据,自带回归功能;不需要复杂的参数设置,直接给出舒服的图形,自带图形风格设计。
fig1, axes = plt.subplots(2, 2, figsize=(10, 8)) # 创建一个 2行 2列的画布
sns.distplot(df['price'], bins=10, ax=axes[0, 0]) # axes[0,1] 左上图
sns.boxplot(df['price'], df['sales'], data=df, ax=axes[0, 1]) # axes[0,1] 右上图
sns.scatterplot(x=df['advertise'], y=df['sales'], ax=axes[1, 0]) # axes[1,0] 左下图
sns.regplot(x=df['difference'], y=df['sales'], ax=axes[1, 1]) # axes[1,1] 右下图
plt.show()
数据文件中收集了 30个月本公司牙膏销售量、价格、广告费用及同期的市场均价。
(1)分析牙膏销售量与价格、广告投入之间的关系,建立数学模型;
(2)估计所建立数学模型的参数,进行统计分析;
(3)利用拟合模型,预测在不同价格和广告费用下的牙膏销售量。
本问题及数据来自:姜启源、谢金星,数学模型(第 3版),高等教育出版社。
本案例在Python数学建模StatsModels统计回归模型数据的准备中就曾出现,文中还提到该文的例程并不是最佳的求解方法和结果。
这是因为该文例程是直接将所有给出的特征变量(销售价格、市场均价、广告费、价格差)都作为自变量,直接进行线性回归。谢金星老师说,这不科学。科学的方法是先分析这些特征变量对目标变量(销量)的影响,然后选择能影响目标的特征变量,或者对特征变量进行适当变换(如:平方、对数)后,再进行线性回归。以下参考视频教程中的解题思路进行分析。
案例问题的数据量很小,数据完整规范,实际上并不需要进行数据探索和数据清洗,不过可以看一下数据的分布特性。例程和结果如下,我是没看出什么名堂来,与正态分布的差距都不小。
# 数据探索:分布特征
fig1, axes = plt.subplots(2, 2, figsize=(10, 8)) # 创建一个 2行 2列的画布
sns.distplot(dfData['price'], bins=10, ax=axes[0,0]) # axes[0,1] 左上图
sns.distplot(dfData['average'], bins=10, ax=axes[0,1]) # axes[0,1] 右上图
sns.distplot(dfData['advertise'], bins=10, ax=axes[1,0]) # axes[1,0] 左下图
sns.distplot(dfData['difference'], bins=10, ax=axes[1,1]) # axes[1,1] 右下图
plt.show()

既然将所有特征变量都作为自变量直接进行线性回归不科学,就要先对每个自变量与因变量的关系进行考察。
# 数据探索:相关性
fig2, axes = plt.subplots(2, 2, figsize=(10, 8)) # 创建一个 2行 2列的画布
sns.regplot(x=dfData['price'], y=dfData['sales'], ax=axes[0,0])
sns.regplot(x=dfData['average'], y=dfData['sales'], ax=axes[0,1])
sns.regplot(x=dfData['advertise'], y=dfData['sales'], ax=axes[1,0])
sns.regplot(x=dfData['difference'], y=dfData['sales'], ax=axes[1,1])
plt.show()
# = 关注 Youcans,分享原创系列 Https://blog.csdn.net/youcans =

单变量线性回归图还是很有价值的。首先上面两图(sales-price,sales-average)的数据点分散,与回归直线差的太远,说明与销量的相关性小——谢金星老师讲课中也是这样分析的。其次下面两图(sales-advertise,sales-difference)的线性度较高,至少比上图好多了,回归直线和置信区间也反映出线性关系。因此,可以将广告费(advertise)、价格差(difference)作为自变量建模进行线性回归。
进一步地,有人观察散点图后认为销量与广告费的关系(sales-advertise)更接近二次曲线,对此也可以通过回归图对 sales 与 advertise 进行高阶多项式回归拟合,结果如下图。

模型1:将所有特征变量都作为自变量直接进行线性回归,这就是《模型数据的准备》中的方案。
模型 2:选择价格差(difference)、广告费(advertise)作为自变量建模进行线性回归。
模型 3:选择价格差(difference)、广告费(advertise)及广告费的平方项作为作为自变量建模进行线性回归。
下段给出了使用不同模型进行线性回归的例程和运行结果。对于这个问题的分析和结果讨论,谢金星老师在视频中讲的很详细,网络上也有不少相关文章。由于本文主要讲可视化,对结果就不做详细讨论了。

数据文件中收集了 30个月本公司牙膏销售量、价格、广告费用及同期的市场均价。
(1)分析牙膏销售量与价格、广告投入之间的关系,建立数学模型;
(2)估计所建立数学模型的参数,进行统计分析;
(3)利用拟合模型,预测在不同价格和广告费用下的牙膏销售量。
# LinearRegression_v4.py
# v4.0: 分析和结果的可视化
# 日期:2021-05-08
# Copyright 2021 YouCans, XUPT
import numpy as np
import pandas as pd
import statsmodels.api as sm
from statsmodels.sandbox.regression.predstd import wls_prediction_std
import matplotlib.pyplot as plt
import seaborn as sns
# 主程序 = 关注 Youcans,分享原创系列 https://blog.csdn.net/youcans =
def main():
# 读取数据文件
readPath = "../data/toothpaste.csv" # 数据文件的地址和文件名
dfOpenFile = pd.read_csv(readPath, header=0, sep=",") # 间隔符为逗号,首行为标题行
# 准备建模数据:分析因变量 Y(sales) 与 自变量 x1~x4 的关系
dfData = dfOpenFile.dropna() # 删除含有缺失值的数据
sns.set_style('dark')
# 数据探索:分布特征
fig1, axes = plt.subplots(2, 2, figsize=(10, 8)) # 创建一个 2行 2列的画布
sns.distplot(dfData['price'], bins=10, ax=axes[0,0]) # axes[0,1] 左上图
sns.distplot(dfData['average'], bins=10, ax=axes[0,1]) # axes[0,1] 右上图
sns.distplot(dfData['advertise'], bins=10, ax=axes[1,0]) # axes[1,0] 左下图
sns.distplot(dfData['difference'], bins=10, ax=axes[1,1]) # axes[1,1] 右下图
plt.show()
# 数据探索:相关性
fig2, axes = plt.subplots(2, 2, figsize=(10, 8)) # 创建一个 2行 2列的画布
sns.regplot(x=dfData['price'], y=dfData['sales'], ax=axes[0,0])
sns.regplot(x=dfData['average'], y=dfData['sales'], ax=axes[0,1])
sns.regplot(x=dfData['advertise'], y=dfData['sales'], ax=axes[1,0])
sns.regplot(x=dfData['difference'], y=dfData['sales'], ax=axes[1,1])
plt.show()
# 数据探索:考察自变量平方项的相关性
fig3, axes = plt.subplots(1, 2, figsize=(10, 4)) # 创建一个 2行 2列的画布
sns.regplot(x=dfData['advertise'], y=dfData['sales'], order=2, ax=axes[0]) # order=2, 按 y=b*x**2 回归
sns.regplot(x=dfData['difference'], y=dfData['sales'], order=2, ax=axes[1]) # YouCans, XUPT
plt.show()
# 线性回归:分析因变量 Y(sales) 与 自变量 X1(Price diffrence)、X2(Advertise) 的关系
y = dfData['sales'] # 根据因变量列名 list,建立 因变量数据集
x0 = np.ones(dfData.shape[0]) # 截距列 x0=[1,...1]
x1 = dfData['difference'] # 价格差,x4 = x1 - x2
x2 = dfData['advertise'] # 广告费
x3 = dfData['price'] # 销售价格
x4 = dfData['average'] # 市场均价
x5 = x2**2 # 广告费的二次元
x6 = x1 * x2 # 考察两个变量的相互作用
# Model 1:Y = b0 + b1*X1 + b2*X2 + e
# # 线性回归:分析因变量 Y(sales) 与 自变量 X1(Price diffrence)、X2(Advertise) 的关系
X = np.column_stack((x0,x1,x2)) # [x0,x1,x2]
Model1 = sm.OLS(y, X) # 建立 OLS 模型: Y = b0 + b1*X1 + b2*X2 + e
result1 = Model1.fit() # 返回模型拟合结果
yFit1 = result1.fittedvalues # 模型拟合的 y 值
prstd, ivLow, ivUp = wls_prediction_std(result1) # 返回标准偏差和置信区间
print(result1.summary()) # 输出回归分析的摘要
print("\nModel1: Y = b0 + b1*X + b2*X2")
print('Parameters: ', result1.params) # 输出:拟合模型的系数
# # Model 2:Y = b0 + b1*X1 + b2*X2 + b3*X3 + b4*X4 + e
# 线性回归:分析因变量 Y(sales) 与 自变量 X1~X4 的关系
X = np.column_stack((x0,x1,x2,x3,x4)) #[x0,x1,x2,...,x4]
Model2 = sm.OLS(y, X) # 建立 OLS 模型: Y = b0 + b1*X1 + b2*X2 + b3*X3 + e
result2 = Model2.fit() # 返回模型拟合结果
yFit2 = result2.fittedvalues # 模型拟合的 y 值
prstd, ivLow, ivUp = wls_prediction_std(result2) # 返回标准偏差和置信区间
print(result2.summary()) # 输出回归分析的摘要
print("\nModel2: Y = b0 + b1*X + ... + b4*X4")
print('Parameters: ', result2.params) # 输出:拟合模型的系数
# # Model 3:Y = b0 + b1*X1 + b2*X2 + b3*X2**2 + e
# # 线性回归:分析因变量 Y(sales) 与 自变量 X1、X2 及 X2平方(X5)的关系
X = np.column_stack((x0,x1,x2,x5)) # [x0,x1,x2,x2**2]
Model3 = sm.OLS(y, X) # 建立 OLS 模型: Y = b0 + b1*X1 + b2*X2 + b3*X2**2 + e
result3 = Model3.fit() # 返回模型拟合结果
yFit3 = result3.fittedvalues # 模型拟合的 y 值
prstd, ivLow, ivUp = wls_prediction_std(result3) # 返回标准偏差和置信区间
print(result3.summary()) # 输出回归分析的摘要
print("\nModel3: Y = b0 + b1*X1 + b2*X2 + b3*X2**2")
print('Parameters: ', result3.params) # 输出:拟合模型的系数
# 拟合结果绘图
fig, ax = plt.subplots(figsize=(8,6)) # YouCans, XUPT
ax.plot(range(len(y)), y, 'b-.', label='Sample') # 样本数据
ax.plot(range(len(y)), yFit3, 'r-', label='Fitting') # 拟合数据
# ax.plot(range(len(y)), yFit2, 'm--', label='fitting') # 拟合数据
ax.plot(range(len(y)), ivUp, '--',color='pink',label="ConfR") # 95% 置信区间 上限
ax.plot(range(len(y)), ivLow, '--',color='pink') # 95% 置信区间 下限
ax.legend(loc='best') # 显示图例
plt.title('Regression analysis with sales of toothpaste')
plt.xlabel('period')
plt.ylabel('sales')
plt.show()
return
if __name__ == '__main__':
main()
OLS Regression Results
==============================================================================
Dep. Variable: sales R-squared: 0.886
Model: OLS Adj. R-squared: 0.878
Method: Least Squares F-statistic: 105.0
Date: Sat, 08 May 2021 Prob (F-statistic): 1.84e-13
Time: 22:18:04 Log-Likelihood: 2.0347
No. Observations: 30 AIC: 1.931
Df Residuals: 27 BIC: 6.134
Df Model: 2
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 4.4075 0.722 6.102 0.000 2.925 5.890
x1 1.5883 0.299 5.304 0.000 0.974 2.203
x2 0.5635 0.119 4.733 0.000 0.319 0.808
==============================================================================
Omnibus: 1.445 Durbin-Watson: 1.627
Prob(Omnibus): 0.486 jarque-Bera (JB): 0.487
Skew: 0.195 Prob(JB): 0.784
Kurtosis: 3.486 Cond. No. 115.
==============================================================================
Model1: Y = b0 + b1*X + b2*X2
Parameters:
const 4.407493
x1 1.588286
x2 0.563482
OLS Regression Results
==============================================================================
Dep. Variable: sales R-squared: 0.895
Model: OLS Adj. R-squared: 0.883
Method: Least Squares F-statistic: 74.20
Date: Sat, 08 May 2021 Prob (F-statistic): 7.12e-13
Time: 22:18:04 Log-Likelihood: 3.3225
No. Observations: 30 AIC: 1.355
Df Residuals: 26 BIC: 6.960
Df Model: 3
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 8.0368 2.480 3.241 0.003 2.940 13.134
x1 1.3832 0.288 4.798 0.000 0.791 1.976
x2 0.4927 0.125 3.938 0.001 0.236 0.750
x3 -1.1184 0.398 -2.811 0.009 -1.936 -0.300
x4 0.2648 0.199 1.332 0.195 -0.144 0.674
==============================================================================
Omnibus: 0.141 Durbin-Watson: 1.762
Prob(Omnibus): 0.932 Jarque-Bera (JB): 0.030
Skew: 0.052 Prob(JB): 0.985
Kurtosis: 2.885 Cond. No. 2.68e+16
==============================================================================
Model2: Y = b0 + b1*X + ... + b4*X4
Parameters:
const 8.036813
x1 1.383207
x2 0.492728
x3 -1.118418
x4 0.264789
OLS Regression Results
==============================================================================
Dep. Variable: sales R-squared: 0.905
Model: OLS Adj. R-squared: 0.894
Method: Least Squares F-statistic: 82.94
Date: Sat, 08 May 2021 Prob (F-statistic): 1.94e-13
Time: 22:18:04 Log-Likelihood: 4.8260
No. Observations: 30 AIC: -1.652
Df Residuals: 26 BIC: 3.953
Df Model: 3
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 17.3244 5.641 3.071 0.005 5.728 28.921
x1 1.3070 0.304 4.305 0.000 0.683 1.931
x2 -3.6956 1.850 -1.997 0.056 -7.499 0.108
x3 0.3486 0.151 2.306 0.029 0.038 0.659
==============================================================================
Omnibus: 0.631 Durbin-Watson: 1.619
Prob(Omnibus): 0.729 Jarque-Bera (JB): 0.716
Skew: 0.203 Prob(JB): 0.699
Kurtosis: 2.362 Cond. No. 6.33e+03
==============================================================================
Model3: Y = b0 + b1*X1 + b2*X2 + b3*X2**2
Parameters:
const 17.324369
x1 1.306989
x2 -3.695587
x3 0.348612
以上就是Python数学建模StatsModels统计回归可视化的详细内容,更多关于数学建模StatsModels统计回归的资料请关注编程网其它相关文章!
--结束END--
本文标题: Python数学建模StatsModels统计回归可视化示例详解
本文链接: https://lsjlt.com/news/154768.html(转载时请注明来源链接)
有问题或投稿请发送至: 邮箱/279061341@qq.com QQ/279061341
2024-03-01
2024-03-01
2024-03-01
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
回答
回答
回答
回答
回答
回答
回答
回答
回答
回答
0