C++示例详解Prim算法与优先队列

2024-04-02 19:04:59 176人浏览安东尼

摘要

目录Prim算法prim代码实现优先队列优先队列代码实现自定义类型优先序列贪心算法的本质是：一个问题的局部最优解，也是该问题的全局最优解。最小生成树的最优子结构性质：假设一个无向图

最小生成树的最优子结构性质：假设一个无向图包含两部分A,B，其中A为最小生成树部分，B为剩余部分，则存在以下性质：该无向图中一个顶点在A部分，另一个顶点在B部分的边中，权值最小的边一定属于整个无向图的最小生成树，即部分最小权值是整个最小生成树的局部最有解，该性质符合贪心算法的特点。

Prim算法

基于最小生成树的该性质，使用prim算法来求解最小生成树。

贪心算法属性：一个局部全优解，也是全局全优解

思想：设T是最小生成树，A<=V,(u,v)是连接着A到A补集（一个在A中，一个不在A中）最小权值的边，则一定是最小生成树边。

prim代码实现

#include <stdio.h>
#include <malloc.h>
#define VERTEXNUM 6
void createGraph(int (*edge)[VERTEXNUM], int start, int end, int value);
void displayGraph(int (*edge)[VERTEXNUM]);
void prim(int (*edge)[VERTEXNUM], int (**tree)[VERTEXNUM], int startVertex, int* vertexStatusArr);
int main(void){
	//动态创建存放边的二维数组  
        int (*edge)[VERTEXNUM] = (int (*)[VERTEXNUM])malloc(sizeof(int)*VERTEXNUM*VERTEXNUM);
        int i,j;
        for(i=0;i<VERTEXNUM;i++){
                for(j=0;j<VERTEXNUM;j++){
                        edge[i][j] = 0;
                }
        }
	//存放顶点的遍历状态，0：未遍历，1：已遍历 
        int* vertexStatusArr = (int*)malloc(sizeof(int)*VERTEXNUM);
        for(i=0;i<VERTEXNUM;i++){
                vertexStatusArr[i] = 0;
        }
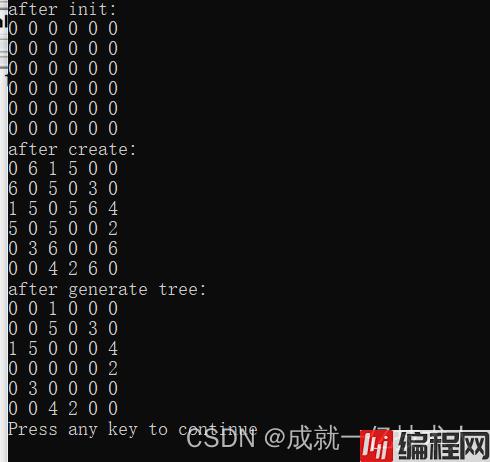
        printf("after init:\n");
        displayGraph(edge);
	//创建图  
        createGraph(edge,0,1,6);
        createGraph(edge,0,3,5);
        createGraph(edge,0,2,1);
        createGraph(edge,1,2,5);
        createGraph(edge,1,4,3);
        createGraph(edge,2,4,6);
        createGraph(edge,2,3,5);
        createGraph(edge,2,5,4);
        createGraph(edge,3,5,2);
        createGraph(edge,4,5,6);
        printf("after create:\n");
        displayGraph(edge);
	//最小生成树
        int (*tree)[VERTEXNUM] = NULL;
        prim(edge, &tree, 0, vertexStatusArr);
        printf("after generate tree:\n");
        displayGraph(tree);
        free(edge);
        free(tree);
        return 0;
}
//创建图
void createGraph(int (*edge)[VERTEXNUM], int start, int end, int value){
        edge[start][end] = value;
        edge[end][start] = value;
}
//打印存储的图
void displayGraph(int (*edge)[VERTEXNUM]){
        int i,j;
        for(i=0;i<VERTEXNUM;i++){
                for(j=0;j<VERTEXNUM;j++){
                        printf("%d ",edge[i][j]);
                }
                printf("\n");
        }
}
void prim(int (*edge)[VERTEXNUM], int (**tree)[VERTEXNUM], int startVertex, int* vertexStatusArr){
	//申请存储树的内存
        *tree = (int (*)[VERTEXNUM])malloc(sizeof(int)*VERTEXNUM*VERTEXNUM);
        int i,j;
        for(i=0;i<VERTEXNUM;i++){
                for(j=0;j<VERTEXNUM;j++){
                       (*tree)[i][j] = 0;
                }
        }
	//从顶点0开始，则顶点0就是已访问的
        vertexStatusArr[0] = 1;
        int least, start, end, vNum = 1;
	//如果还顶点还没有访问完
        while(vNum < VERTEXNUM){
                least = 9999;
                for(i=0;i<VERTEXNUM;i++){
			//选择已经访问过的点
                        if(vertexStatusArr[i] == 1){
                                for(j=0;j<VERTEXNUM;j++){
					//选择一个没有访问过的点
                                        if(vertexStatusArr[j] == 0){
						//选出一条value最小的边
                                                if(edge[i][j] != 0 && edge[i][j] < least){
                                                        least = edge[i][j];
                                                        start = i;
                                                        end = j;
                                                }
                                        }
                                }
                        }
                }
                vNum++;
		//将点设置为访问过
                vertexStatusArr[end] = 1;
		//将边加到树中
                createGraph(*tree,start,end,least);
        }
}

结果

优先队列

普通的队列是一种先进先出的数据结构，元素在队列尾追加，而从队列头删除。

优先队列中，元素被赋予优先级。当访问元素时，具有最高优先级的元素最先删除。优先队列具有最高级先出（first in, largest out）的行为特征。

优先队列代码实现

基本类型优先序列

#include <iOStream>
#include <queue>
using namespace std;
//方法1
struct tmp1 //运算符重载<
{
    int x;
    tmp1(int a) {x = a;}
    bool operator<(const tmp1& a) const
    {
        return x < a.x; //大顶堆
    }
};
//方法2
struct tmp2 //重写仿函数
{
    bool operator() (tmp1 a, tmp1 b)
    {
        return a.x < b.x; //大顶堆
    }
};
int main()
{
    tmp1 a(1);
    tmp1 b(2);
    tmp1 c(3);
    priority_queue<tmp1> d;
    d.push(b);
    d.push(c);
    d.push(a);
    while (!d.empty())
    {
        cout << d.top().x << '\n';
        d.pop();
    }
    cout << endl;
    priority_queue<tmp1, vector<tmp1>, tmp2> f;
    f.push(b);
    f.push(c);
    f.push(a);
    while (!f.empty())
    {
        cout << f.top().x << '\n';
        f.pop();
    }
}

自定义类型优先序列

#include <iostream>
#include <queue>
using namespace std;
//方法1
struct tmp1 //运算符重载<
{
    int x;
    tmp1(int a) {x = a;}
    bool operator<(const tmp1& a) const
    {
        return x < a.x; //大顶堆
    }
};
//方法2
struct tmp2 //重写仿函数
{
    bool operator() (tmp1 a, tmp1 b)
    {
        return a.x < b.x; //大顶堆
    }
};
int main()
{
    tmp1 a(1);
    tmp1 b(2);
    tmp1 c(3);
    priority_queue<tmp1> d;
    d.push(b);
    d.push(c);
    d.push(a);
    while (!d.empty())
    {
        cout << d.top().x << '\n';
        d.pop();
    }
    cout << endl;
    priority_queue<tmp1, vector<tmp1>, tmp2> f;
    f.push(b);
    f.push(c);
    f.push(a);
    while (!f.empty())
    {
        cout << f.top().x << '\n';
        f.pop();
    }
}

结果