目录算法的主题思想:1. 动态连通性2. 定义问题3. quick-find算法实现算法分析4. quick-uNIOn算法实现森林表示算法分析5.加权 quick-uni
1.优秀的算法因为能够解决实际问题而变得更为重要;
2.高效算法的代码也可以很简单;
3.理解某个实现的性能特点是一个挑战;
4.在解决同一个问题的多种算法之间进行选择时,科学方法是一种重要的工具;
5.迭代式改进能够让算法的效率越来越高效;
动态连接:输入是一对整数对的序列,其中每个整数代表某种类型的对象(或触点),我们将整数对p q 解释为意味着p连接到q。我们假设“连接到”是等价关系:
等价关系将对象划分为多个等价类 或连接的组件。等价类称为连通分量或分量。
我们的目标是编写一个程序,以从序列中过滤掉多余的对:当程序从输入中读取整数对 p q时,只有在该对点不等价的情况下,才应将对写入到输出中,并且将p连接到q。如果等价,则程序应忽略整数对pq 并继续读取下对。
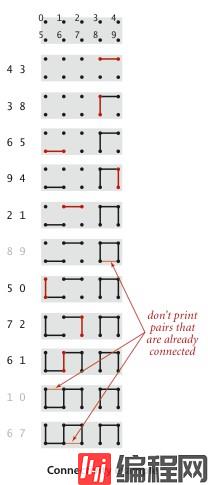
动态连通性问题的应用:
在更高的抽象层次上,可以将输入的所有整数看做属于不同的数学集合。
设计算法的第一个任务就是精确地定义问题。
算法解决的问题越大,它完成任务所需的时间和空间可能越多。我们不可能预先知道这其间的量化关系,通常只会在发现解决问题很困难,或是代价巨大,或是发现算法所提供的信息比原问题所需要的更加有用时修改问题。例如,连通性问题只要求我们的程序能够判断出给定的整数对是否相连,但并没有要求给出两者之间的通路上的所有连接。这样的要求更难,并会得出另一组不同的算法。
为了定义和说明问题,先设计一份api 来封装基本操作: 初始化,连接两个触点,查找某个触点的分量 ,判断两个触点是否属于同一分量,分量的数量:
/// <summary>
/// 动态连通API
/// </summary>
public interface IUnionFind
{
/// <summary>
/// 连接
/// </summary>
/// <param name="p"></param>
/// <param name="q"></param>
void Union(int p, int q);
/// <summary>
/// 查找触点 p 的分量标识符
/// </summary>
/// <param name="p"></param>
/// <returns></returns>
int Find(int p);
/// <summary>
/// 判断两个触点是否处于同一分量
/// </summary>
/// <param name="p"></param>
/// <param name="q"></param>
/// <returns></returns>
bool Connected(int p, int q);
/// <summary>
/// 连通分量的数量
/// </summary>
/// <returns></returns>
int Count();
}为解决动态连通性问题设计算法的任务转化为实现这份API:
数据结构的性质会直接影响算法的效率。这里,以触点为索引,触点和连接分量都是用 int 值表示,将会使用分量中某个触点的值作为分量的标识符。所以,一开始,每个触点都是只含有自己的分量,分量标识符为触点的值。由此,可以初步实现一部分方法:
public class FirstUnionFind:IUnionFind
{
private int[] id;//* 分量id 以触点作为索引
private int count;//分量数量
public FirstUnionFind(int n)
{
count = n;
id = new int[n];
for (var i = 0; i < n; i++)
{
id[i] = i; // 第一个 i 作为触点,第二个 i 作为触点的值
}
}
public int Count()
{
return count;
}
public bool Connected(int p, int q)
{
return Find(p) == Find(q);
}
public int Find(int p)
{
}
public void Union(int p, int q)
{
}
}Union-find 的成本模型 是数组的访问次数(无论读写)。
quick-find 算法是保证当且仅当 id[p] 等于 id[q] 时,p 和 q 是连通的。也就是说,在同一个连通分量中的所有触点在 id[ ] 中的值全部相等。
所以Find 方法只需返回id[q],Union 方法需要先判断Find(p) 是否等于Find(q) ,若相等直接返回;若不相等,需要将 q 所在的连通分量中所有触点的 id [ ] 值全部更新为 id[p]。
public class QuickFindUF: IUnionFind
{
private int[] id;//* 分量id 以触点作为索引
private int count;//分量数量
public QuickFindUF(int n)
{
count = n;
id = new int[n];
for (var i = 0; i < n; i++)
{
id[i] = i; // 第一个 i 作为触点,第二个 i 作为触点的值
}
}
public int Count()
{
return count;
}
public bool Connected(int p, int q)
{
return Find(p) == Find(q);
}
public int Find(int p)
{
return id[p];
}
public void Union(int p, int q)
{
var pID = Find(p);
var qID = Find(q);
if (pID == qID)
return;
for (var i = 0; i < id.Length; i++)
{
if (id[i] == qID)
id[i] = pID;
}
count--; //连通分量减少
}
public void Show()
{
for(var i = 0;i<id.Length;i++)
Console.WriteLine("索引:"+i+",值:"+ id[i] );
Console.WriteLine("连通分量数量:"+count);
}
}
Find() 方法只需访问一次数组,所以速度很快。但是对于处理大型问题,每对输入 Union() 方法都需要扫描整个数组。
每一次归并两个分量的 Union() 方法访问数组的次数在 N+3 到 2N+1 之间。由代码可知,两次 Find 操作访问两次数组,扫描数组会访问N次,改变其中一个分量中所有触点的值需要访问 1 到 N - 1 次(最好情况是该分量中只有一个触点,最坏情况是该分量中有 N - 1个触点),2+N+N-1。
如果使用quick-find 算法来解决动态连通性问题并且最后只得到一个连通分量,至少需要调用 N-1 次Union() 方法,那么至少需要 (N+3)(N-1) ~ N^2 次访问数组,是平方级别的。
quick-union 算法重点提高 union 方法的速度,它也是基于相同的数据结构 -- 已触点为索引的 id[ ] 数组,但是 id[ ] 的值是同一分量中另一触点的索引(名称),也可能是自己(根触点)——这种联系成为链接。
在实现 Find() 方法时,从给定触点,链接到另一个触点,知道到达根触点,即链接指向自己。同时修改 Union() 方法,分别找到 p q 的根触点,将其中一个根触点链接到根触点。
public class QuickUnionUF : IUnionFind
{
private int[] id;
private int count;
public QuickUnionUF(int n)
{
count = n;
id = new int[n];
for (var i = 0; i < n; i++)
{
id[i] = i; // 第一个 i 作为触点,第二个 i 作为触点的值
}
}
public int Count()
{
return count;
}
public bool Connected(int p, int q)
{
return Find(p) == Find(q);
}
public int Find(int p)
{
while (p != id[p])
p = id[p];
return p;
}
public void Union(int p, int q)
{
var pRoot = Find(p);
var qRoot = Find(q);
if (pRoot == qRoot)
return;
id[pRoot] =qRoot;
count--; //连通分量减少
}
public void Show()
{
for (var i = 0; i < id.Length; i++)
Console.WriteLine("索引:" + i + ",值:" + id[i]);
Console.WriteLine("连通分量数量:" + count);
}
}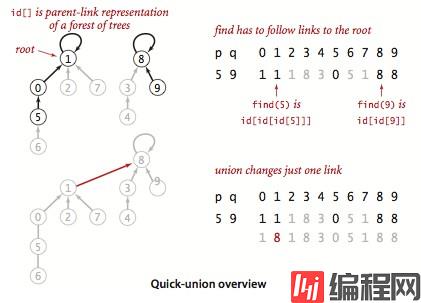
id[ ] 数组用父链接的形式表示一片森林,用节点表示触点。无论从任何触点所对应的节点随着链接查找,最后都将到达含有该节点的根节点。初始化数组之后,每个节点的链接都指向自己。
定义:一棵树的大小是它的节点的数量。树中一个节点的深度是它到根节点的路径上链接数。树的高度是它的所有节点中的最大深度。
quick-union 算法比 quick-find 算法更快,因为它对每对输入不需要遍历整个数组。
分析quick-union 算法的成本比 quick-find 算法的成本要困难,因为quick-union 算法依赖于输入的特点。在最好的情况下,find() 方法只需访问一次数组就可以得到一个触点的分量表示;在最坏情况下,需要 2i+1 次数组访问(i 时触点的深度)。由此得出,该算法解决动态连通性问题,在最佳情况下的运行时间是线性级别,最坏情况下的输入是平方级别。解决了quick-find 算法中 union() 方法总是线性级别,解决动态连通性问题总是平方级别。
quick-union 算法中 find() 方法访问数组的次数为 1(到达根节点只需访问一次) 加上 给定触点所对应节点的深度的两倍(while 循环,一次读,一次写)。union() 访问两次 find() ,如果两个触点不在同一分量还需加一次写数组。
假设输入的整数对是有序的 0-1, 0-2,0-3 等,N-1 对之后N个触点将全部处于相同的集合之中,且得到的树的高度为 N-1。由上可知,对于整数对 0-i , find() 访问数组的次数为 2i + 1,因此,处理 N 对整数对所需的所有访问数组的总次数为 3+5+7+ ......+(2N+1) ~ n^2
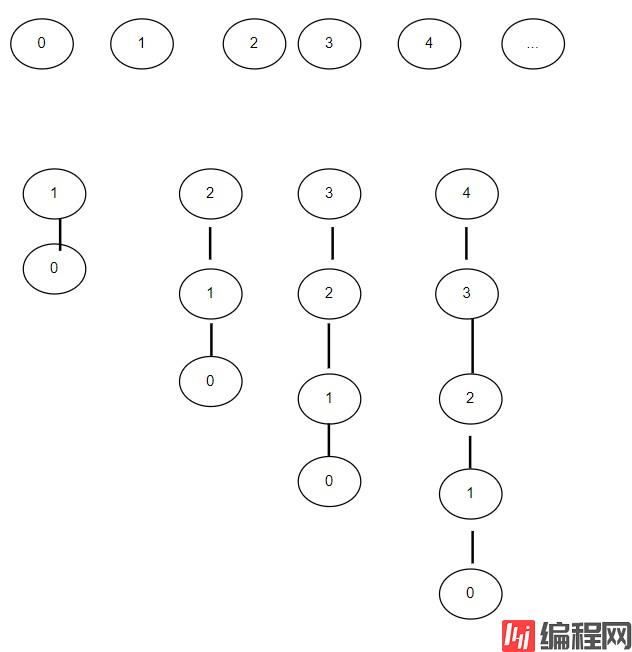
简单改动就可以避免 quick-union算法 出现最坏情况。quick-union算法 union 方法是随意将一棵树连接到另一棵树,改为总是将小树连接到大树,这需要记录每一棵树的大小,称为加权quick-union算法。
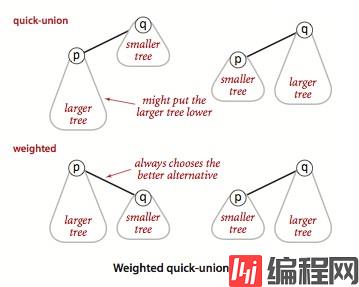
代码:
public class WeightedQuickUnionUF: IUnionFind
{
int[] sz;//以触点为索引的 各个根节点对应的分量树大小
private int[] id;
private int count;
public WeightedQuickUnionUF(int n)
{
count = n;
id = new int[n];
sz = new int[n];
for (var i = 0; i < n; i++)
{
id[i] = i; // 第一个 i 作为触点,第二个 i 作为触点的值
sz[i] = 1;
}
}
public int Count()
{
return count;
}
public bool Connected(int p, int q)
{
return Find(p) == Find(q);
}
public int Find(int p)
{
while (p != id[p])
p = id[p];
return p;
}
public void Union(int p, int q)
{
var pRoot = Find(p);
var qRoot = Find(q);
if (pRoot == qRoot)
return;
if (sz[pRoot] < sz[qRoot])
{
id[pRoot] = qRoot;
}
else
{
id[qRoot] = pRoot;
}
count--; //连通分量减少
}
public void Show()
{
for (var i = 0; i < id.Length; i++)
Console.WriteLine("索引:" + i + ",值:" + id[i]);
Console.WriteLine("连通分量数量:" + count);
}
}加权 quicj-union 算法最坏的情况:
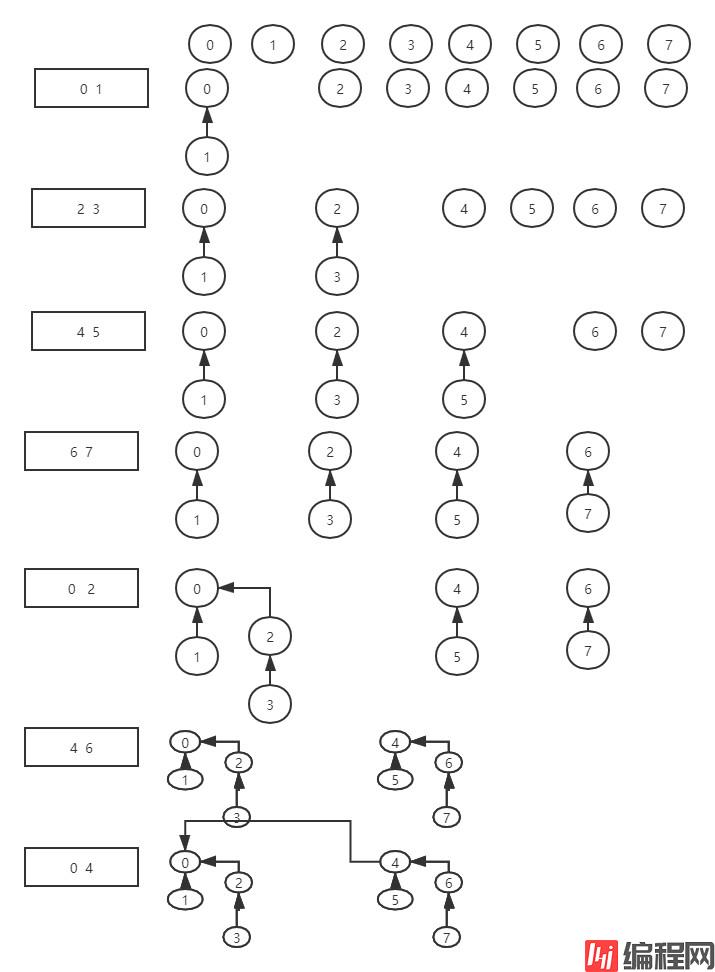
这种情况,将要被归并的树的大小总是相等的(且总是 2 的 冥),都含有 2^n 个节点,高度都正好是 n 。当归并两个含有 2^n 个节点的树时,得到的树含有 2 ^ n+1 个节点,高度增加到 n+1 。
节点大小: 1 2 4 8 2^k = N
高 度: 0 1 2 3 k
k = logN
所以加权 quick-union 算法可以保证对数级别的性能。
对于 N 个触点,加权 quick-union 算法构造的森林中的任意节点的深度最多为logN。
对于加权 quick-union 算法 和N 个触点,在最坏情况下 find,connected 和 union 方法的成本的增长量级为 logN。
对于动态连通性问题,加权 quick-union 算法 是三种算法中唯一可以用于解决大型问题的算法。加权 quick-union 算法 处理 N 个触点和 M 条连接时最多访问数组 c M logN 次,其中 c 为常数。
三个算法处理一百万个触点运行时间对比:
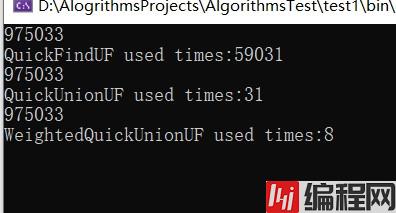
三个算法性能特点:

在检查节点的同时将它们直接连接到根节点。
实现:为 find 方法添加一个循环,将在路径上的所有节点都直接链接到根节点。完全扁平化的树。
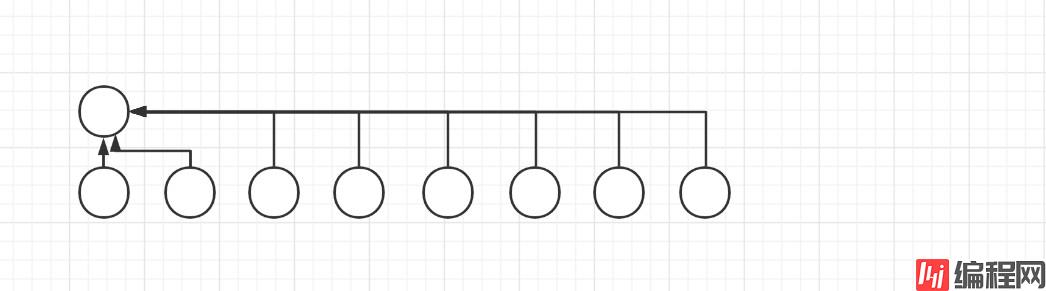
研究各种基础问题的基本步骤:
到此这篇关于C#并查集(union-find)算法的文章就介绍到这了。希望对大家的学习有所帮助,也希望大家多多支持编程网。
--结束END--
本文标题: C#并查集(union-find)算法详解
本文链接: https://lsjlt.com/news/146151.html(转载时请注明来源链接)
有问题或投稿请发送至: 邮箱/279061341@qq.com QQ/279061341
2024-03-01
2024-03-01
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
回答
回答
回答
回答
回答
回答
回答
回答
回答
回答
0