目录写在前面石子合并写在前面 之前讲过背包问题,线性DP,区间DP,不知道大家忘了吗,这次是计数类DP 石子合并 老规矩,先画图。 思路:把1,2,3, … n分别
之前讲过背包问题,线性DP,区间DP,不知道大家忘了吗,这次是计数类DP
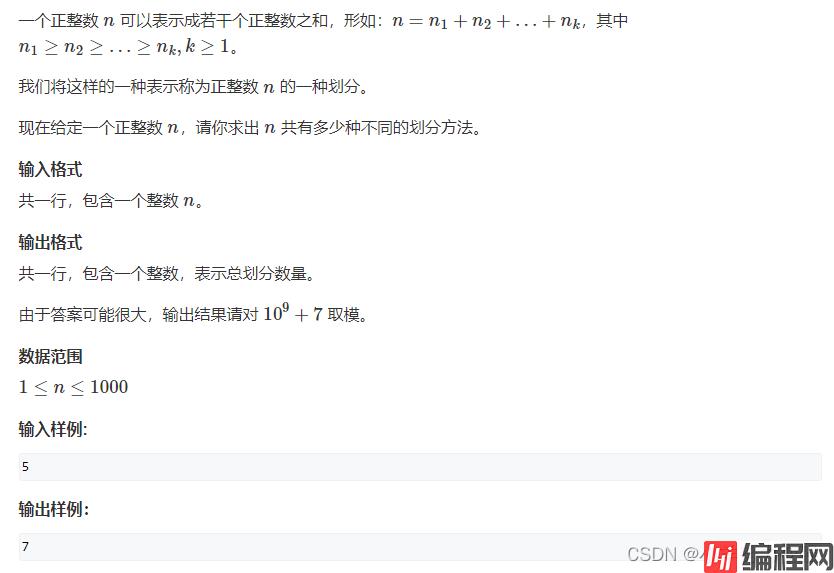

老规矩,先画图。
思路:把1,2,3, … n分别看做n个物体的体积,这n个物体均无使用次数限制,问恰好能装满总体积为n的背包的总方案数(完全背包问题变形)
初值问题:
求最大值时,当都不选时,价值显然是 0
而求方案数时,当都不选时,方案数是 1(即前 i 个物品都不选的情况也是一种方案),所以需要初始化为 1
即:for (int i = 0; i <= n; i ++) f[i][0] = 1;
等价变形后: f[0] = 1
状态计算:
f[i][j]表示前i个整数(1,2…,i)恰好拼成j的方案数
求方案数:把集合选0个i,1个i,2个i,…全部加起来
f[i][j] = f[i - 1][j] + f[i - 1][j - i] + f[i - 1][j - 2 * i] + …;
f[i][j - i] = f[i - 1][j - i] + f[i - 1][j - 2 * i] + …;
因此 f[i][j]=f[i−1][j]+f[i][j−i]; (这一步类似完全背包的推导)
朴素做法
// f[i][j] = f[i - 1][j] + f[i][j - i]
#include <bits/stdc++.h>
using namespace std;
const int N = 1e3 + 7, mod = 1e9 + 7;
int f[N][N];
int main() {
int n;
cin >> n;
for (int i = 0; i <= n; i ++) {
f[i][0] = 1; // 容量为0时,前 i 个物品全不选也是一种方案
}
for (int i = 1; i <= n; i ++) {
for (int j = 0; j <= n; j ++) {
f[i][j] = f[i - 1][j] % mod; // 特殊 f[0][0] = 1
if (j >= i) f[i][j] = (f[i - 1][j] + f[i][j - i]) % mod;
}
}
cout << f[n][n] << endl;
}
等价变形
// f[i][j] = f[i - 1][j] + f[i][j - i]
#include <bits/stdc++.h>
using namespace std;
const int N = 1e3 + 7, mod = 1e9 + 7;
int f[N];
int main() {
int n;
cin >> n;
f[0] = 1; // 容量为0时,前 i 个物品全不选也是一种方案
for (int i = 1; i <= n; i ++) {
for (int j = i; j <= n; j ++) {
f[j] = (f[j] + f[j - i]) % mod;
}
}
cout << f[n] << endl;
}
上面是完全背包问题的解法,再来看看不用完全背包问题求解
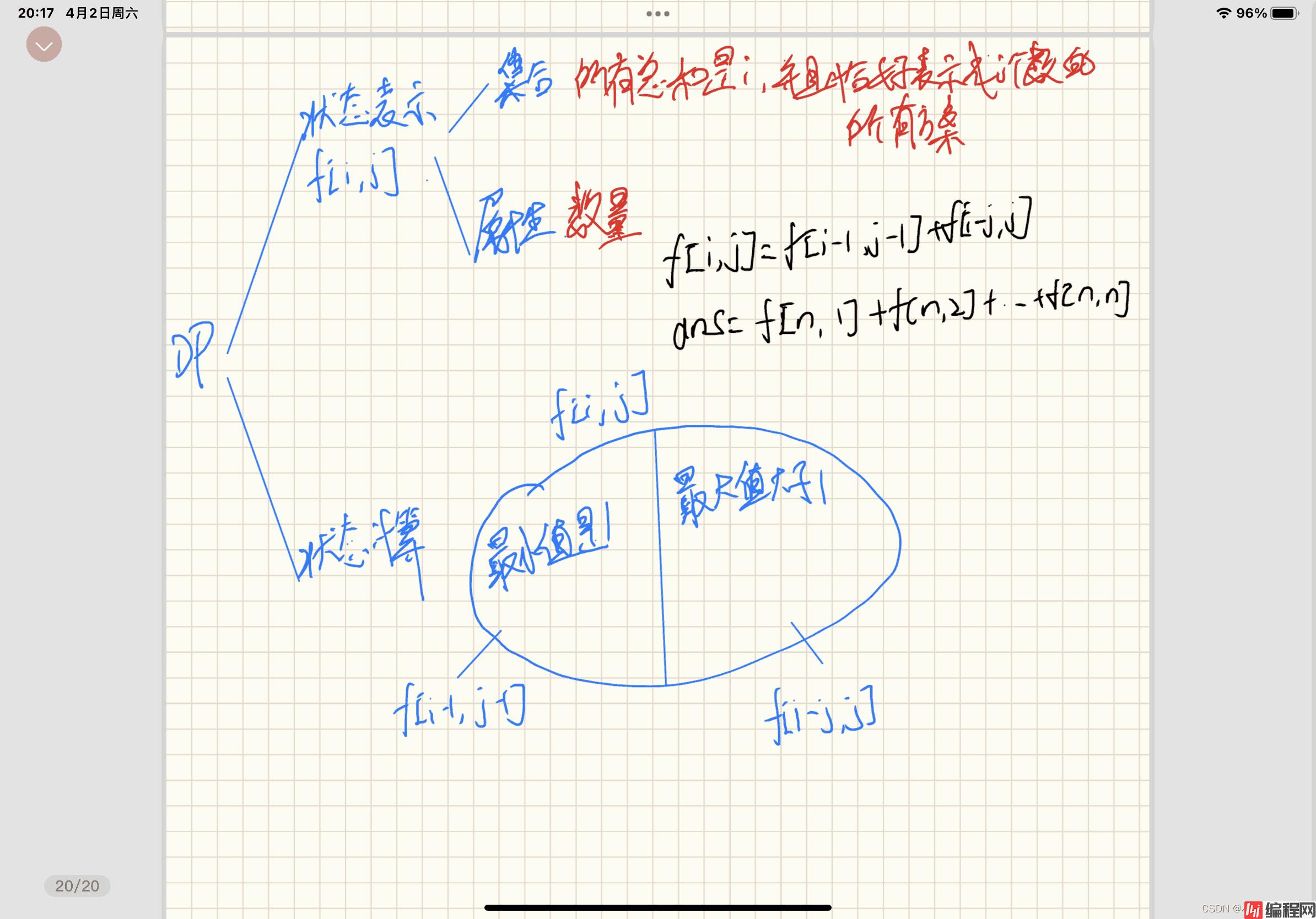
状态计算:分两部分
综上所述:f[i][j] = f[i - 1][j - 1] + f[i - j][j];
//非背包做法
//状态表示:f[i][j] 所有总和是i,并且恰好可以表示成j个数的和的方案
#include <bits/stdc++.h>
using namespace std;
const int N = 1010, mod = 1e9 + 7;
int n;
int f[N][N];
int main()
{
cin >> n;
f[0][0] = 1;
for (int i = 1; i <= n; i ++ )
//i最多表示成i个数的和,因此j<=i
for (int j = 1; j <= i; j ++ )
f[i][j] = (f[i - 1][j - 1] + f[i - j][j]) % mod;
int res = 0;
for (int i = 1; i <= n; i ++ ) res = (res + f[n][i]) % mod;
cout << res << endl;
return 0;
}
到此这篇关于C语言 深入理解动态规划之计数类DP的文章就介绍到这了,更多相关C语言 计数类DP内容请搜索编程网以前的文章或继续浏览下面的相关文章希望大家以后多多支持编程网!
--结束END--
本文标题: C语言 深入理解动态规划之计数类DP
本文链接: https://lsjlt.com/news/145730.html(转载时请注明来源链接)
有问题或投稿请发送至: 邮箱/279061341@qq.com QQ/279061341
2024-03-01
2024-03-01
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
回答
回答
回答
回答
回答
回答
回答
回答
回答
回答
0