Python 官方文档:入门教程 => 点击学习
目录1.双摆问题2.运动过程3.公式推导过程1.双摆问题 所谓双摆,就是两个连在一起的摆。 接下来本来是要推公式的,考虑考虑到大家可能会有公式恐惧症,同时又喜欢看图,所以把公式挪
所谓双摆,就是两个连在一起的摆。


接下来本来是要推公式的,考虑考虑到大家可能会有公式恐惧症,同时又喜欢看图,所以把公式挪到后面。
所以,只需知道角速度的微分方程,就可写出对应的代码,其方程如下:

从而转为代码得到:
# 其中,lam,mu,G_L1,M为全局变量
def derivs(state, t):
dydx = np.zeros_like(state)
th1,om1,th2,om2 = state
dydx[0] = state[1]
delta = state[2] - state[0]
cDelta, sDelta = np.cos(delta), np.sin(delta)
sTh1,_,sTh2,_ = np.sin(state)
den1 = M - mu*cDelta**2
dydx[1] = (mu * om1**2 * sDelta * cDelta
+ mu * G_L1 * sTh2 * cDelta
+ mu * lam * om2**2 * sDelta
- M * G_L1 * sTh1)/ den1
dydx[2] = state[3]
den2 = lam * den1
dydx[3] = (- mu * lam * om2**2 * sDelta * cDelta
+ M * G_L1 * sTh1 * cDelta
- M * om1**2 * sDelta
- M * G_L1 * sTh2)/ den2
return dydx接下来根据微分方程的解,便可进行绘图。
# 这段代码用于设置初值,并调用integrate求解微分方程组
import numpy as np
import scipy.integrate as integrate
G = 9.8
L1,L2 = 1.0, 1.0
G_L1 = G/L1
lam = L2/L1 #杆长度比L2/L1
mu = 1.0 #质量比M2/M1
M = 1+mu
# 生成时间
dt = 0.01
t = np.arange(0, 20, dt)
th1,th2 = 120.0, -10.0 #初始角度
om1,om2 = 0.0, 0.00 #初始角速度
state = np.radians([th1, om1, th2, om2])
# 微分方程组数值解
y = integrate.odeint(derivs, state, t)
# 真实坐标
x1 = L1*sin(y[:, 0])
y1 = -L1*cos(y[:, 0])
x2 = L2*sin(y[:, 2]) + x1
y2 = -L2*cos(y[:, 2]) + y1
至此,就得到了所有位置处的坐标,从而可以观察到双摆的轨迹如图所示
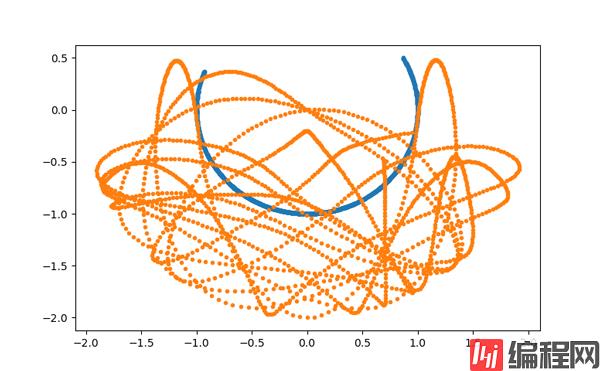
绘图代码为:
import matplotlib.pyplot as plt
plt.scatter(x1,y1,marker='.')
plt.scatter(x2,y2,marker='.')
plt.show()若将时间设置得长一点,然后在画图的时候更改一下颜色,就会看到双摆的运动区间,可见自然界还是挺有情怀的

其绘图代码为:
plt.plot(x1,y1,marker='.',alpha=0.2, linewidth=0.2)
plt.plot(x2,y2,marker='.',alpha=0.2, linewidth=2, c='r')
plt.axis('off')
plt.show()当然,也可以将其运动轨迹以一种三维的形式绘制出来
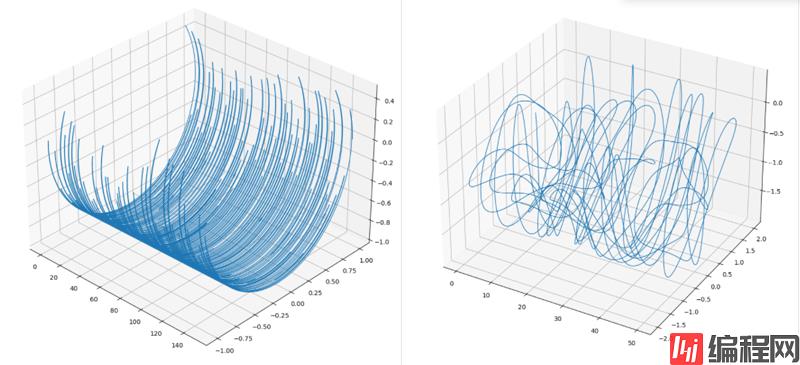
额……好吧,看来并没有什么情怀。
但是,如果把这两个小球分别当作两个星球,而我们又在一颗星球上,那么所观测到的另一颗星球的运动大致如下,不出意外是个圆,毕竟圆形二者之间的距离是恒定的。

绘图代码为:
ax = plt.gca(projection='3d')
ax.plot3D(t,x2-x1,y2-y1,linewidth=0.5)
plt.show()如果更改一下初值,则图形将有如下变化
初值设为:
th1,th2 = 0, 0 #初始角度
om1,om2 = 120.0, 108.00 #初始角速度最后,还是传统技能,绘制一下双摆的运动过程如下:

代码为:
import matplotlib.animation as animation
# 下面为绘图过程
fig = plt.figure(figsize=(12,12))
ax = fig.add_subplot(111, autoscale_on=False, xlim=(-2, 2), ylim=(-2, 2))
ax.set_aspect('equal')
ax.grid()
line, = ax.plot([], [], 'o-', lw=2)
time_template = 'time = %.1fs'
time_text = ax.text(0.05, 0.9, '', transfORM=ax.transAxes)
# 初始化图形
def init():
line.set_data([], [])
time_text.set_text('')
return line, time_text
def animate(i):
thisx = [0, x1[i], x2[i]]
thisy = [0, y1[i], y2[i]]
line.set_data(thisx, thisy)
time_text.set_text(time_template % (i*dt))
return line, time_text
ani = animation.FuncAnimation(fig, animate, range(1, len(y)),
interval=dt*1000, blit=True, init_func=init)
ani.save("dua_1.gif",writer='imagemagick')
plt.show()双摆的动能和势能分别为:


根据拉格朗日方程

则有:
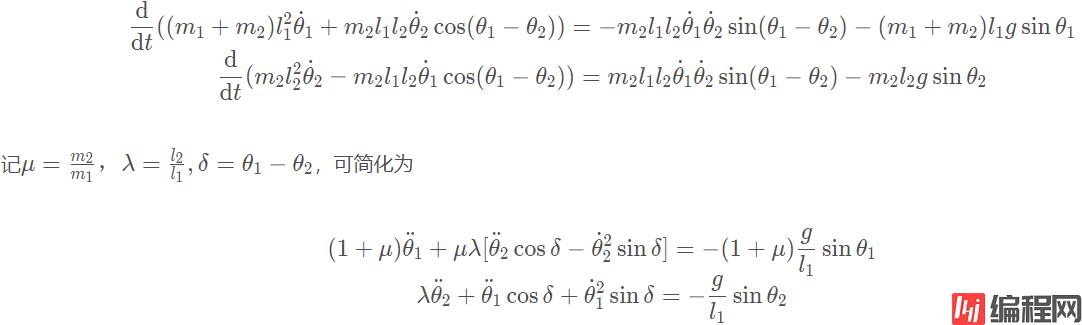

其中,

展开可得则:

到此这篇关于利用python画双摆的文章就介绍到这了,更多相关Python画双摆内容请搜索编程网以前的文章或继续浏览下面的相关文章希望大家以后多多支持编程网!
--结束END--
本文标题: 利用Python绘画双摆操作分享
本文链接: https://lsjlt.com/news/144711.html(转载时请注明来源链接)
有问题或投稿请发送至: 邮箱/279061341@qq.com QQ/279061341
2024-03-01
2024-03-01
2024-03-01
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
回答
回答
回答
回答
回答
回答
回答
回答
回答
回答
0