Python 官方文档:入门教程 => 点击学习
目录1.前言
归一化算法NORMalization将数据处理成量纲一直的数据,一般限定在[0,1]、[-1,1]
一般在进行建模的时候需要进行数据归一化处理,
原因如下:
下面介绍三种常见的标准化方法,分别是最大最小值、正态中心化、小数点定标
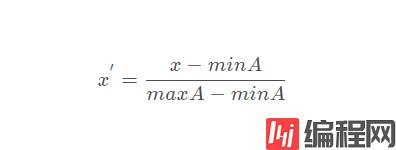
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 1.最小最大标准化
Data = np.array([[0.2,0.9,29],
[0.9,0.1,100],
[0.5,0.5,30]]) #最小-最大归一化算法
# 1.1数据转化
def MinMax(data):
min = 0
max = 1
C = data[:,2]
min = np.min(C)
max = np.max(C)
for one in data:
one[2] = (one[2]-min) / (max-min)
print('转化后的矩阵:\n',data)
return data
# 1.2可视化
def ShowData(Data,ShowD1):
length = len(Data)
X = np.ones(Data.shape[0])
plt.figure(1)
plt.subplot(121)
for i in range(length):
plt.scatter(X*(i+1),Data[:,i])
plt.subplot(122)
for i in range(length):
plt.scatter(X*(i+1),ShowD1[:,i])
plt.show()
ShowData(Data,MinMax(Data.copy()))转化后的矩阵:
[[0.2 0.9 0. ]
[0.9 0.1 1. ]
[0.5 0.5 0.01408451]]

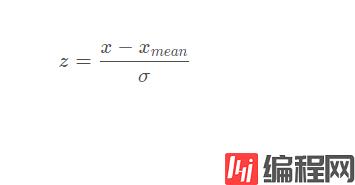
def Zscore(data):
x_mean = np.mean(data[:2])
length = len(data[:,2])
vari = np.sqrt((np.sum((data[:2]-x_mean)**2))/length)
print('方差:',vari)
data[:,2] = (data[:,2]-x_mean)/vari
print('Z-score标准化后的矩阵是',data)
return data
ShowData(Data,Zscore(Data.copy()))方差: 51.569160680908254
Z-score标准化后的矩阵是 [[0.2 0.9 0.13864876]
[0.9 0.1 1.5154406 ]
[0.5 0.5 0.15804019]]


# 小数定标归一化算法
def Decimals(data):
C = np.abs(data[:,2])
max = int(np.sort(C)[-1]) # 按从小到大排序,取最后一位,及最大值
k = len(str(max))
print('绝对值最大的位数:\n',k)
data[:2] = data[:,2] /(10**k)
print('小数点定标准化后的矩阵:\n',data)
return data
ShowData(Data,Decimals(Data.copy()))绝对值最大的位数:
3
小数点定标准化后的矩阵:
[[2.9e-02 1.0e-01 3.0e-02]
[2.9e-02 1.0e-01 3.0e-02]
[5.0e-01 5.0e-01 3.0e+01]]

到此这篇关于python实现归一化算法详情的文章就介绍到这了,更多相关Python归一化算法内容请搜索编程网以前的文章或继续浏览下面的相关文章希望大家以后多多支持编程网!
--结束END--
本文标题: Python实现归一化算法详情
本文链接: https://lsjlt.com/news/143091.html(转载时请注明来源链接)
有问题或投稿请发送至: 邮箱/279061341@qq.com QQ/279061341
2024-03-01
2024-03-01
2024-03-01
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
回答
回答
回答
回答
回答
回答
回答
回答
回答
回答
0