目录需求背景需求实现功能拓展高级实现结果总结需求背景 在一些主流app上有一些比较特殊的滤镜效果,例如灰尘、塑料封面、光影效果等。在此之前一直困惑这类滤镜效果是如何实现的,单纯gls
在一些主流app上有一些比较特殊的滤镜效果,例如灰尘、塑料封面、光影效果等。在此之前一直困惑这类滤镜效果是如何实现的,单纯glsl脚本来绘制难度似乎有点大。例如下面截取平台的几种效果像是在图片上方覆盖了一个透明图层。



glsl脚本实现其实特别简单,加载两个纹理同时对两个纹理的rgb进行相加即可。
void main() {
vec2 uv = gl_FraGCoord.xy / iResolution.xy;
vec4 texture1 = texture(iChannel1,uv);
vec4 texture2 = texture(iChannel2,uv);
vec3 rgb = texture1.rgb + texture2.rgb;
vec4 pixel = vec4(rgb,1.);
gl_FragColor = pixel;
}
纹理1

纹理2
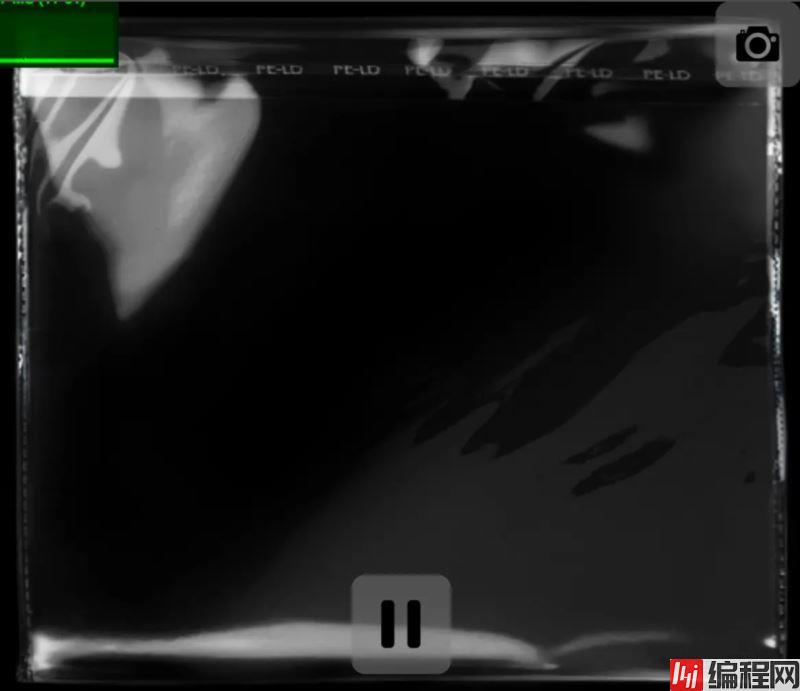
纹理3

纹理2是一个透明塑封封面,两者rgb叠加即可呈现出最终希望达到的效果。这样的效果似乎比通过脚本模拟更加简易,同时也降低了开发成本。
另外对于素材和图片尺寸的问题是可以通过脚本代码来处理完成。对uv1和uv2进行比例相乘计算处理即可实现图片尺寸缩放操作,此外再通过smoothstep方法和算法控制纹理显示区域大小实现了框中图的效果。
void main()
{
vec2 uv1 = gl_FragCoord.xy / iResolution.xy;
uv1.y = mod(uv1.y, 1.0);
vec2 uv2 = uv1;
uv1 -= 0.5;
uv1 *= 2.;
uv1 += 0.5;
uv2 -= 0.5;
uv2 *= 1.5;
uv2 += 0.5;
float l = 0.003;
float k = smoothstep((1.0 - l), (1.0 - l) + 0.006, uv1.x);
float k1 = smoothstep(l, l - 0.006, uv1.x);
float m = smoothstep((1.0 - l), (1.0 - l) + 0.006, uv1.y);
float m1 = smoothstep(l, l - 0.006, uv1.y);
float i = smoothstep((1.0 - l), (1.0 - l) + 0.006, uv2.x);
float i1 = smoothstep(l, l - 0.006, uv2.x);
float j = smoothstep((1.0 - l), (1.0 - l) + 0.006, uv2.y);
float j1 = smoothstep(l, l - 0.006, uv2.y);
vec4 texture1 = texture(iChannel1, uv1)* (1.0 - k) * (1.0 - k1) * (1.0 - m) * (1.0 - m1);
vec4 texture2 = texture(iChannel3, vec2(uv2.x,uv2.y)) * (1.0 - i) * (1.0 - i1) * (1.0 - j) * (1.0 - j1);
gl_FragColor = 1.0 - (1.0 - texture1) * (1.0 - texture2);
}
此外还能对素材图片进行替换,从而达到不同效果场景氛围。
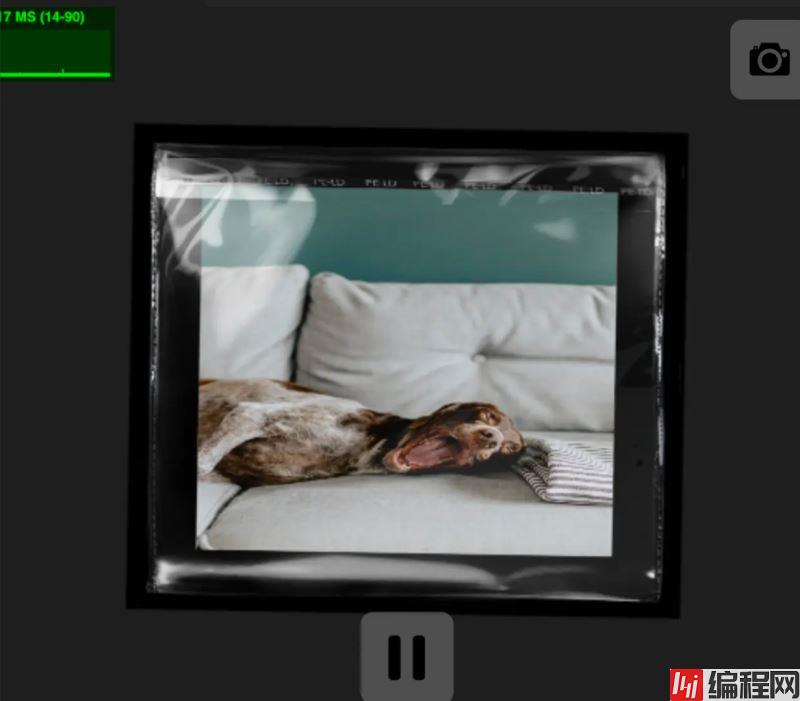
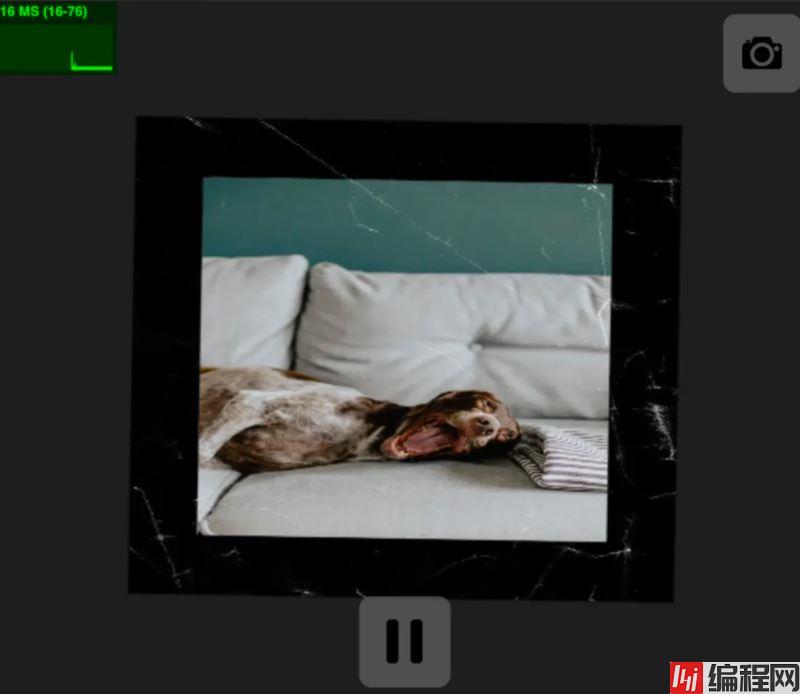
但不一定所有效果都需要借助于设计师素材来实现,高级玩法其实是可以通过脚本直接实现。例如下面光照效果实际上就是只通过代码模拟来完成的,没有增加外置任何其他素材资源。但是实现成本较高需要了解很多数学模拟公式以及技术背景,而且最终效果也不一定是产品和设计所能满意的。

PS:具体实现是从shaderToy上找到,这里就不分享具体代码了。
有感而发在需求实现上原先因为设计希望实现彩虹、光照、物件等在原图之上的滤镜效果,在此调研之前一直觉得技术是可以完成所有任务的。最终通过实践才发现有时候一些捷径实现和更直接简单的方法或许是最终最优解。所以技术和设计还是息息相关,在时间和精力有限的情况下应该借助其他方式快速达成需求目标。
到此这篇关于OpenGL Shader实现物件材料效果详解的文章就介绍到这了,更多相关OpenGL Shader物件材料效果内容请搜索编程网以前的文章或继续浏览下面的相关文章希望大家以后多多支持编程网!
--结束END--
本文标题: OpenGLShader实现物件材料效果详解
本文链接: https://lsjlt.com/news/140155.html(转载时请注明来源链接)
有问题或投稿请发送至: 邮箱/279061341@qq.com QQ/279061341
2024-01-21
2023-10-28
2023-10-28
2023-10-27
2023-10-27
2023-10-27
2023-10-27
回答
回答
回答
回答
回答
回答
回答
回答
回答
回答
0