Python极值整数的边界探讨分析

第一次接触 python 时，是把它作为一个智能计算器使用的。普通的计算器计算很大的数时都会报错，比如计算 9 的 531441 次方，计算器就提示我不是数字：

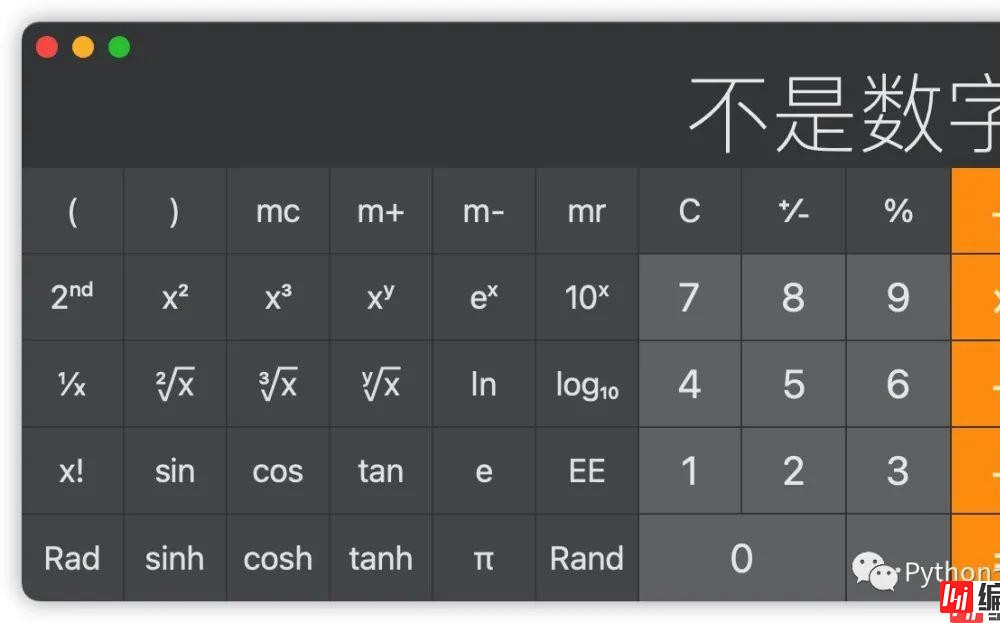
然后我就试了下 Python 解释器

这个数字共有 507124 位，50 万位，不吃不喝不睡，1 秒钟读一位，要读 5 天多，足以说明，Python 中的整数是没有边界的，只是数越大，计算时间的越长而已。

但是，在编程的时候，如果要取最小值，通常要定义一个变量 min，初始值设置为最大，然后计算的结果比这个 min 小的时候，就把这个结果赋值给 min，那如何在 Python 中定义这个初始值呢？

比如说，在 Java 中，我们有 Integer.MIN_VALUE 和 Integer.MAX_VALUE，Python 有类似的固定值么？

答：有，虽然 Python 中的 int 是没有边界的，但是如果你只需要一个比其他数字更大的数字，你可以使用 float('inf')， 以类似的方式，比其他所有数字都小：float('-inf') ，这种方法适用于 Python 2 和 3。

>>> float('inf') > 10**100
True
>>> float('-inf') < - 10**100
True
>>>

不过，Java 的 Long.MAX_VALUE 相当于 python3 的 sys.maxsize 和 Python2 的 sys.maxint，Java 的 Long.MIN_VALUE 相当于 Python3 的 -sys.maxsize -1  和 Python2 -sys.maxint - 1。

>>> sys.maxsize
9223372036854775807
>>> -sys.maxsize-1
-9223372036854775808
>>>

最后的话

Python 中 float('inf') 和 float('-inf') 代表着无穷大和无穷小，是真正的极值，是不是很完美的数学表达？我觉得这也是一种 Python 之美吧。

以上就是Python极值整数的边界探讨分析的详细内容，更多关于Python极值整数的边界的资料请关注编程网其它相关文章！