Qt Quick QML-500行代码实现合成大西瓜游戏

"合成大西瓜"这个游戏在年前很火热，还上过微博热搜，最近便玩了一阵还挺有意思的,所以研究了一下小球碰撞原理,自己亲自手写碰撞算法来实现一个合成大西瓜游戏.并支持任意大小布局,你想玩多大面积,就拖多大面积,只要面积够大,认真玩下去,合100个大西瓜都可以.哈哈~~~

1.游戏介绍

游戏里面总共有11个水果,两个相同水果的合成一个较大的水果,最终合成一个大西瓜便不能继续合下去了:

然而博主自己写的游戏,自己都合不出一个大西瓜来.

如果看起来很模糊,或者看不到视频,可以直接去https://www.bilibili.com/video/BV1eh411Y7uV/哔哩哔哩直接看.

代码中逻辑主要如下所示:

移动水果,并进行边界检测计算水果之间碰撞检测,如果是两个相同的水果,则进行水果合并,否则就计算小球碰撞后的移动方向.判断水果是否溢出终点线,如果溢出,则将每个水果进行破碎,弹出结束画面,等待下一局

而水果碰撞计算是里面较为复杂的,所以我接下来给大家来讲解小球碰撞算法之前,我们首先来复习下以前学过的向量.

2.向量介绍

我们以下面向量为例:

那么此时的向量就是,那么他们的内容就是(B.x-A.x,B.y-A.y),当我们对向量取绝对值时,就是求A坐标到B坐标的长度,也就是:

斜线长度 =

3. 单位向量

单位向量就是长度为1的一个向量.还是以这个向量为例(长度为C):

如果想获取的单位向量,那么他们的内容为 :((B.x-A.x)/C, (B.y-A.y) /C)

所以的单位向量就等于1

4. 向量与单位向量点乘

向量与单位向量点乘,是用来获取向量在单位向量上的投影.

首先向量与向量点乘的公式如下所示:

其中是向量和向量之间的夹角.

假如是单位向量,那么绝对值就等于1.

所以：

$\vec{a}* \vec{b} = \left | \vec{a} \right | cos\theta$

最终如下图所示:

红色的线表示的长度.我们从俯视图来看,红色线不正是向量在向量方向上的投影吗?

假如两个向量是收尾相连,那么角度就是单位向量沿生出来后的角度,如下图所示:

得出结论:

• 夹角如果为钝角,那么为负数.(单位向量的反方向)
• 夹角如果为锐角,那么为正数(单位向量的正方向)

5.小球碰撞情景

• 由于两个小球碰撞,切线上的速度都是互相平行的,没有作用力(如下图所示).
• 而连心线上是相互碰撞的(如下图所示),会有作用力,所以我们只需要求出球1和球2的连心线方向上的速度值.
• 然后再根据动量守恒定律和机械能守恒定律求出碰撞后的球1和球2的连心线方向.
• 最后再互相加上各自在切线上的速度即可得到各自碰撞后的x速度,y速度.

碰撞前如下图所示:

• v1n和v1t : 是球1在连心线方向和切线方向上的投影速度
• v2n和v2t : 是球2在连心线方向和切线方向上的投影速度
• v1 : 球1的速度方向,等于v1n + v1t
• v2 : 球2的速度方向,等于v2n + v2t

5.1 获取v1n和v2n

之前我们已证明过:向量与单位向量点乘,是用来获取向量在单位向量上的投影.

所以代码如下所示:

let distance = Math.sqrt(Math.pow((ball1.pointX - ball2.pointX),2) + Math.pow((ball1.pointY - ball2.pointY),2));
let radius = ball1.r + ball2.r;
let dx = ball1.pointX - ball2.pointX
let dy = ball1.pointY - ball2.pointY

let ex = dx / radius;
let ey = dy / radius;       // 获取连心线的单位向量（ex,ey） 

let v1n = ex * ball1.vx + ey * ball1.vy   
let v2n = ex * ball2.vx + ey * ball2.vy

5.2 计算碰撞后的速度方向

首先我们来看下碰撞后如下图所示:

• v1' : 球1碰撞后的速度方向,等于v1n' + v1t
• v2 ' : 球2碰撞后的的速度方向,等于v2n' + v2t
• v1n'和v2n' : 两个小球碰撞后的投影速度

假如这两个小球是一样大, v1n'和v2n'取值就是:

v1n' = v2n

v2n' = v1n

并且根据动量守恒定律和机械能守恒定律得出:

• v1和v2 : 两个小球碰前速度.
• m1和m2 : 两个小球的质量
• v1'和v2' : 两个小球碰后速度

所以最终碰撞函数代码如下所示:

let distance = Math.sqrt(Math.pow((ball1.pointX - ball2.pointX),2) + Math.pow((ball1.pointY - ball2.pointY),2));
    let radius = ball1.r + ball2.r;
    let dx = ball1.pointX - ball2.pointX

    let dy = ball1.pointY - ball2.pointY

    let ex = dx / radius; let ey = dy / radius;       // 获取连心线的单位向量（ex,ey）  (单位向量就是长度为1的一条线)

    let v1n = ex * ball1.vx + ey * ball1.vy           
    let v2n = ex * ball2.vx + ey * ball2.vy
    if(v1n >= v2n)  return;                      // 在小球擦肩而过情景中,会描述为什么要加这一句
    let v1nn = ball1.cor * ((ball1.mass - ball2.mass) * v1n + 2 *ball2.mass *v2n ) / (ball1.mass +ball2.mass)  // 碰撞后公式
    let v2nn = ball2.cor * ((ball2.mass - ball1.mass) * v2n + 2 *ball1.mass *v1n ) / (ball1.mass +ball2.mass)
 
    let ux = -dy / radius; let uy = dx / radius;       
    let v1t =ux * ball1.vx + uy*ball1.vy        
    let v2t = ux * ball2.vx + uy * ball2.vy

    ball1.vx = v1nn*ex +v1t*ux;       
    ball1.vy = v1nn*ex +v1t*uy;

    ball2.vx = v2nn*ex +v2t*ux;
　  ball2.vy = v2nn*ex +v2t*uy;

6. 小球擦肩而过情景

首先我们来看看下面两个小球平行移动场景图:

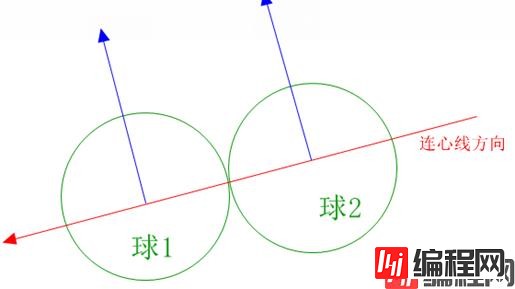
假如球1和球2在平行移动,那么他们与连心线的夹角恰好是90°, v1n和v2n则都为0

假如球1的夹角大于了球2的夹角,那么就会出现碰撞,如下图所示:

虚线箭头速度方向表示球1的夹角大于球2的夹角的时候场景.

而cos的取值方式刚好是在0~180°的时候,角度越大,值越小,所以v1n >=v2n时,则不会碰撞.

7. 小球一直降落在所有小球的正上方情景

效果图如下所示:

这时候,小球由于没有切线上的速度方向,所以在重力加速度下,会慢慢让小球们堆起来,从而游戏结束.

所以我们还要在碰撞后末尾添加以下判断:

if (v1n == 0 && v1t ==0 && v2t == 0) {      // 当v1n为0,说明小球1静止不动,而v1t和v2t为0,说明球1和球2在切线上没有速度方向,球2位于球1的正上方,此时需要给球2一个vx偏移值,避免小球们堆起来

        ball2.vx += 0.1

 }

修改后效果图所下所示:

整个的碰撞算法实现就完成了,其它逻辑就非常依葫芦画瓢实现即可,代码还在上传中,如果大家还想实现什么小游戏,可以给我留言哦,感兴趣的话,我就撸一个出来.

以上就是Qt Quick QML-500行代码实现的详细内容，更多关于Qt Quick QML-500行代码实现"合成大西瓜游戏"的资料请关注编程网其它相关文章！