本文实例为大家分享了Unity3D实现模型随机切割的具体代码,供大家参考,具体内容如下 模型切割的效果图如下: 我们都知道,模型是由一个个小三角形面组成的,因此我们不妨将问题简化
本文实例为大家分享了Unity3D实现模型随机切割的具体代码,供大家参考,具体内容如下
模型切割的效果图如下:


我们都知道,模型是由一个个小三角形面组成的,因此我们不妨将问题简化,先实现个小目标,完成单个三角形的切割,甚至继续细分成求一条线段与某个平面的交点。
三角形与切割平面的位置关系主要有以下三种:
1. 三角形与切割平面有两个交点,一个交点在顶点上,一个交点在边上。这时,原有的三角形将被分成两个三角形,分别为013、042。
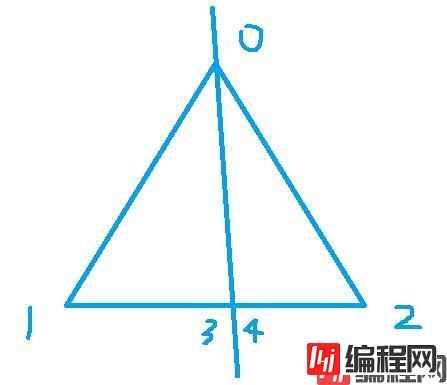
2. 三角形与切割平面有两个交点,两个交点都在边上。这时,原有的三角形将被分成三个三角形,分别为:034、561、126。

3. 其它(无交点、三角形完全在切割平面上、一条边在切割平面上)
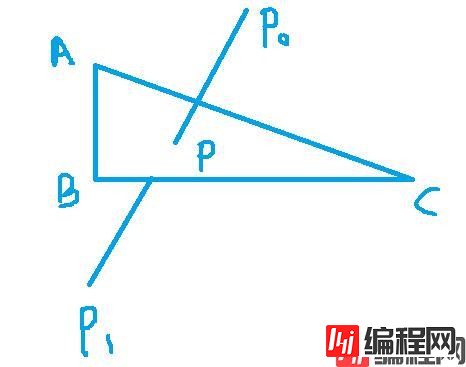
那么,我们如何求线段与平面的交点呢?
即已知平面ABC,线段P0P1,求交点P。
故:
N为平面ABC法向量,可得:N= AB X AC;
P在P0P1上,可得:P = P0 + t * L; L = P1 - P0;
又因P在平面ABC上,可得: N * PA = 0;
代入得:
=> N * (A - P0 + t * L) = 0;
=> N * (A - P0) + t * N * L = 0;
=> t = (P0 - A) * N / (N * L);
=> t = (P0 - A) * (AB X AC) / (N * (P1 - P0));
最终求得P坐标,因为P0P1是线段而非直线,所以我们需要再做个判断,P是否在线段P0P1中间,用向量点乘可轻易实现。
具体代码如下,其中abc为切割平面上的三个顶点(确保必定构成一个平面):
public static GameObject[] Split(GameObject obj, Vector3 a, Vector3 b, Vector3 c)
{
if(obj == null)
{
return null;
}
MeshFilter filter = obj.GetComponent<MeshFilter>();
if(filter == null)
{
return null;
}
//切割面位置调整为相对于模型的本地坐标
a = a - obj.transfORM.position;
b = b - obj.transform.position;
c = c - obj.transform.position;
List<Vector3> vertices = new List<Vector3>(filter.mesh.vertices);
List<int> triangles = new List<int>(filter.mesh.triangles);
List<Vector2> uvs = new List<Vector2>(filter.mesh.uv);
for (int i = 0; i < filter.mesh.triangles.Length; i = i + 3)
{
//取三角形;
Vector3[] p = new Vector3[3];
for (int m = 0; m < 3; m++)
{
p[m] = filter.mesh.vertices[filter.mesh.triangles[i + m]];
}
//0 1 2
//1 2 0 ==> 切割每条边,判断是否有交点,如有交点,在交点处生成两个新的顶点:L/R
//2 0 1
//凡是顶点与平面相交的,一律以新顶点替换
//判断以交点为其中一个顶点的三角形在面的哪一面
//指定:交点到其它顶点形成的向量与平面法向量方向一致,则使用L,否则使用R
//无交点
//其中一个顶点在平面上
//其中的一条边在平面上
//整个三角形都在平面上
List<Point> cross = new List<Point>();
for (int m = 0; m < 3; m++)
{
//求线段与面的交点-无交点返回null
Point tpoint = MathfUtils.LineCrossPlane(p[m], p[(m + 1) % 3], a, b, c);
//排除线段两个端点与平面相交的情况;
if (MathfUtils.PointAtPlane(p[m], a, b, c) || MathfUtils.PointAtPlane(p[(m + 1) % 3], a, b, c))
{
cross.Add(null);
continue;
}
cross.Add(tpoint);
}
int tcount = cross.FindAll(t => t != null).Count;
if (tcount == 0)
{
//完全没交点;
continue;
}
if(tcount == 1)
{
//只与一条边有交点;
//012 tidx = 0 交点x在 0-1上,则有三角形 02x 12x
//012 tidx = 1 交点x在 1-2上,则有三角形 01x 02x
//012 tidx = 2 交点x在 2-3上,则有三角形 01x 12x
int tidx = cross.FindIndex(t => t != null);
if(tidx < 0)
{
continue;
}
vertices.Add(cross[tidx].GetVector3());
vertices.Add(cross[tidx].GetVector3());
Vector2 tuv = (uvs[triangles[i + tidx]] + uvs[triangles[i + (tidx + 1) % 3]]) * 0.5f;
uvs.Add(tuv);
uvs.Add(tuv);
//计算法线,保证新三角形与原来的三角形法线保持一致;
Vector3 nor0 = Vector3.Cross((p[1] - p[0]).normalized, (p[2] - p[0]).normalized);
//改一个
triangles[i + 0] = filter.mesh.triangles[i + tidx];
triangles[i + 1] = filter.mesh.triangles[i + (tidx + 2) % 3];
triangles[i + 2] = vertices.Count - 2;
Vector3 nor1 = Vector3.Cross((vertices[triangles[i + 1]] - vertices[triangles[i + 0]]).normalized,
(vertices[triangles[i + 2]] - vertices[triangles[i + 0]]).normalized);
if(Vector3.Dot(nor0, nor1) < 0)
{
//使用法线方向判断三角形顶点顺序是否与原来一致
int tpidx = triangles[i + 1];
triangles[i + 1] = triangles[i + 2];
triangles[i + 2] = tpidx;
}
//新增一个
triangles.Add(filter.mesh.triangles[i + (tidx + 1) % 3]);
triangles.Add(filter.mesh.triangles[i + (tidx + 2) % 3]);
triangles.Add(vertices.Count - 1);
Vector3 nor2 = Vector3.Cross((vertices[triangles[triangles.Count - 2]] - vertices[triangles[triangles.Count - 3]]).normalized,
(vertices[triangles[triangles.Count - 1]] - vertices[triangles[triangles.Count - 3]]).normalized);
if (Vector3.Dot(nor0, nor2) < 0)
{
int tpidx = triangles[triangles.Count - 1];
triangles[triangles.Count - 1] = triangles[triangles.Count - 2];
triangles[triangles.Count - 2] = tpidx;
}
}
if(tcount == 2)
{
//与两条边有交点;
//012 tidx = 0 交点xy不在 0-1上,则有三角形 xy2 xy1 01y
//012 tidx = 1 交点xy不在 1-2上,则有三角形 xy0 xy2 12y
//012 tidx = 2 交点xy不在 2-3上,则有三角形 xy1 xy0 01y
// x-y-tidx+2 是独立三角形,使用一组顶点
int tidx = cross.FindIndex(t => t == null);
if (tidx < 0)
{
continue;
}
//计算法线,保证新三角形与原来的三角形法线保持一致;
Vector3 nor0 = Vector3.Cross((p[1] - p[0]).normalized, (p[2] - p[0]).normalized);
//x
vertices.Add(cross[(tidx + 1) % 3].GetVector3());
vertices.Add(cross[(tidx + 1) % 3].GetVector3());
Vector2 tuvx = (uvs[triangles[i + (tidx + 1) % 3]] + uvs[triangles[i + (tidx + 2) % 3]]) * 0.5f;
uvs.Add(tuvx);
uvs.Add(tuvx);
//y
vertices.Add(cross[(tidx + 2) % 3].GetVector3());
vertices.Add(cross[(tidx + 2) % 3].GetVector3());
Vector2 tuvy = (uvs[triangles[i + tidx]] + uvs[triangles[i + (tidx + 2) % 3]]) * 0.5f;
uvs.Add(tuvy);
uvs.Add(tuvy);
//改一个
triangles[i + 0] = filter.mesh.triangles[i + (tidx + 2) % 3];
triangles[i + 1] = vertices.Count - 4;
triangles[i + 2] = vertices.Count - 2;
Vector3 nor1 = Vector3.Cross((vertices[triangles[i + 1]] - vertices[triangles[i + 0]]).normalized,
(vertices[triangles[i + 2]] - vertices[triangles[i + 0]]).normalized);
if (Vector3.Dot(nor0, nor1) < 0)
{
int tpidx = triangles[i + 1];
triangles[i + 1] = triangles[i + 2];
triangles[i + 2] = tpidx;
}
//新增一个
triangles.Add(filter.mesh.triangles[i + (tidx + 1) % 3]);
triangles.Add(vertices.Count - 3);
triangles.Add(vertices.Count - 1);
Vector3 nor2 = Vector3.Cross((vertices[triangles[triangles.Count - 2]] - vertices[triangles[triangles.Count - 3]]).normalized,
(vertices[triangles[triangles.Count - 1]] - vertices[triangles[triangles.Count - 3]]).normalized);
if (Vector3.Dot(nor0, nor2) < 0)
{
int tpidx = triangles[triangles.Count - 1];
triangles[triangles.Count - 1] = triangles[triangles.Count - 2];
triangles[triangles.Count - 2] = tpidx;
}
//新增一个
triangles.Add(filter.mesh.triangles[i + tidx % 3]);
triangles.Add(filter.mesh.triangles[i + (tidx + 1) % 3]);
triangles.Add(vertices.Count - 1);
Vector3 nor3 = Vector3.Cross((vertices[triangles[triangles.Count - 2]] - vertices[triangles[triangles.Count - 3]]).normalized,
(vertices[triangles[triangles.Count - 1]] - vertices[triangles[triangles.Count - 3]]).normalized);
if (Vector3.Dot(nor0, nor3) < 0)
{
int tpidx = triangles[triangles.Count - 1];
triangles[triangles.Count - 1] = triangles[triangles.Count - 2];
triangles[triangles.Count - 2] = tpidx;
}
}
}
//根据顶点索引数组确定mesh被分成了几份
//经实验:不可行;因为同一个位置的点在不同的面中是不同的点,无法判断这两个三角形是否是连接起来的
//故只能按方向将模型分成两个
List<List<int>> ntriangles = new List<List<int>>();
List<List<int>> temps = new List<List<int>>();
List<List<Vector3>> nvertices = new List<List<Vector3>>();
List<List<Vector2>> nuvs = new List<List<Vector2>>();
//切割面的法向量;
Vector3 pnormal = Vector3.Cross((c - a).normalized, (b - a).normalized);
ntriangles.Add(new List<int>());
ntriangles.Add(new List<int>());
temps.Add(new List<int>());
temps.Add(new List<int>());
nuvs.Add(new List<Vector2>());
nuvs.Add(new List<Vector2>());
nvertices.Add(new List<Vector3>());
nvertices.Add(new List<Vector3>());
for (int i = 0; i < triangles.Count; i = i + 3)
{
//判断新的三角形在面的哪一侧;
float t = 0;
for(int j = 0; j < 3; j++)
{
Vector3 dir = (vertices[triangles[i + j]] - a).normalized;
float tt = Vector3.Dot(dir, pnormal);
t = Mathf.Abs(tt) > Mathf.Abs(t) ? tt : t;
}
int tidx = t >= 0 ? 0 : 1;
for (int j = 0; j < 3; j++)
{
int idx = temps[tidx].IndexOf(triangles[i + j]);
if (idx < 0)
{
ntriangles[tidx].Add(nvertices[tidx].Count);
nvertices[tidx].Add(vertices[triangles[i + j]]);
temps[tidx].Add(triangles[i + j]);
nuvs[tidx].Add(uvs[triangles[i + j]]);
continue;
}
ntriangles[tidx].Add(idx);
}
}
if(nvertices[0].Count == 0 || nvertices[1].Count == 0)
{
//没有切割到物体
return null;
}
//生成新的模型;
List<GameObject> items = new List<GameObject>();
MeshRenderer render = obj.GetComponent<MeshRenderer>();
for (int i = 0; i < ntriangles.Count; i++)
{
GameObject tobj = new GameObject(i.ToString());
tobj.transform.position = obj.transform.position;
items.Add(tobj);
MeshFilter fi = tobj.AddComponent<MeshFilter>();
MeshRenderer mr = tobj.AddComponent<MeshRenderer>();
if(render != null)
{
mr.material = render.material;
}
Mesh mesh = new Mesh();
mesh.vertices = nvertices[i].ToArray();
mesh.triangles = ntriangles[i].ToArray();
mesh.uv = nuvs[i].ToArray();
mesh.RecalculateNormals();
mesh.RecalculateTangents();
mesh.RecalculateBounds();
fi.mesh = mesh;
}
return items.ToArray();
} --结束END--
本文标题: Unity3D实现模型随机切割
本文链接: https://lsjlt.com/news/121795.html(转载时请注明来源链接)
有问题或投稿请发送至: 邮箱/279061341@qq.com QQ/279061341
2024-03-01
2024-03-01
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
回答
回答
回答
回答
回答
回答
回答
回答
回答
回答
0