PID原理与python的简单实现和调参

2024-04-02 19:04:59 501人浏览安东尼

Python 官方文档：入门教程 => 点击学习

摘要

目录一、前言二、PID控制算法详解2.1 比例控制算法2.1.1 比例控制python简单示意2.1.2 比例控制存在的一些问题2.2 积分控制算法(消除稳态误差)2.2.1 Pyt

一、前言

近期在实际项目中使用到了PID控制算法，于是就该算法做一总结。

二、PID控制算法详解

2.1 比例控制算法

例子: 假设一个水缸，需要最终控制水缸的水位永远维持在1米的高度。

水位目标：T 当前水位：Tn 加水量：U 误差：error error=T-Tn 比例控制系数：kp U = k_p * errorU=kp∗error initial: T=1; Tn=0.2, error=1-0.2=0.8; kp=0.4

2.1.1 比例控制python简单示意

T=1
Tn=0.2
error=1-0.2
kp=0.4

for t in range(1, 10):
    U = kp * error
    Tn += U
    error = T-Tn
    print(f't={t} | add {U:.5f} => Tn={Tn:.5f} error={error:.5f}')
   
"""
t=1 | add 0.32000 => Tn=0.52000 error=0.48000
t=2 | add 0.19200 => Tn=0.71200 error=0.28800
t=3 | add 0.11520 => Tn=0.82720 error=0.17280
t=4 | add 0.06912 => Tn=0.89632 error=0.10368
t=5 | add 0.04147 => Tn=0.93779 error=0.06221
t=6 | add 0.02488 => Tn=0.96268 error=0.03732
t=7 | add 0.01493 => Tn=0.97761 error=0.02239
t=8 | add 0.00896 => Tn=0.98656 error=0.01344
t=9 | add 0.00537 => Tn=0.99194 error=0.00806
"""

2.1.2 比例控制存在的一些问题

根据kp取值不同，系统最后都会达到1米，只不过kp大了达到的更快。不会有稳态误差。若存在漏水情况，在相同情况下，经过多次加水后，水位会保持在0.75不在再变化,因为当U和漏水量一致的时候将保持不变——即稳态误差 U=k_p*error=0.1 => error = 0.1/0.4 = 0.25U=kp∗error=0.1=>error=0.1/0.4=0.25，所以误差永远保持在0.25

T=1
Tn=0.2
error=1-0.2
kp=0.4
extra_drop = 0.1

for t in range(1, 100):
    U = kp * error
    Tn += U - extra_drop
    error = T-Tn
    print(f't={t} | add {U:.5f} => Tn={Tn:.5f} error={error:.5f}')

"""
t=95 | add 0.10000 => Tn=0.75000 error=0.25000
t=96 | add 0.10000 => Tn=0.75000 error=0.25000
t=97 | add 0.10000 => Tn=0.75000 error=0.25000
t=98 | add 0.10000 => Tn=0.75000 error=0.25000
t=99 | add 0.10000 => Tn=0.75000 error=0.25000
"""

实际情况中，这种类似水缸漏水的情况往往更加常见

比如控制汽车运动，摩擦阻力就相当于是"漏水"
控制机械臂、无人机的飞行，各类阻力和消耗相当于"漏水"

所以单独的比例控制，很多时候并不能满足要求

2.2 积分控制算法(消除稳态误差)

比例+积分控制算法：

误差累计
积分控制系数

2.2.1 python简单实现

T=1
Tn=0.2
error=1-0.2
kp=0.4
extra_drop = 0.1
ki=0.2
sum_error = 0

for t in range(1, 20):
    sum_error += error
    U = kp * error + ki * sum_error
    Tn += U - extra_drop
    error = T-Tn
    print(f't={t} | add {U:.5f} => Tn={Tn:.5f} error={error:.5f}')


"""
t=14 | add 0.10930 => Tn=0.97665 error=0.02335
t=15 | add 0.11025 => Tn=0.98690 error=0.01310
t=16 | add 0.10877 => Tn=0.99567 error=0.00433
t=17 | add 0.10613 => Tn=1.00180 error=-0.00180
t=18 | add 0.10332 => Tn=1.00512 error=-0.00512
t=19 | add 0.10097 => Tn=1.00608 error=-0.00608
"""

2.3 微分控制算法(减少控制中的震荡)

在越靠近目标的时候则加的越少。

kd: 微分控制系数
d_error/d_t ~= error_t - error_t_1：误差的变化

3.3.1 加入微分控制算法的python简单示意

令：kd=0.2; d_error = 当前时刻误差-前时刻误差

T=1
Tn=0.2
error=1-0.2
kp=0.4
extra_drop = 0.1

ki=0.2
sum_error = 0

kd=0.2
d_error = 0
error_n = 0
error_b = 0

for t in range(1, 20):
    error_b = error_n
    error_n = error
    # print(error_b1, error_b2)
    d_error = error_n - error_b if t >= 2 else 0
    sum_error += error
    U = kp * error + ki * sum_error + kd * d_error
    Tn += U - extra_drop
    error = T-Tn
    print(f't={t} | add {U:.5f} => Tn={Tn:.5f} error={error:.5f} | d_error: {d_error:.5f}')

"""
t=14 | add 0.09690 => Tn=0.96053 error=0.03947 | d_error: 0.01319
t=15 | add 0.10402 => Tn=0.96455 error=0.03545 | d_error: 0.00310
t=16 | add 0.10808 => Tn=0.97263 error=0.02737 | d_error: -0.00402
t=17 | add 0.10951 => Tn=0.98214 error=0.01786 | d_error: -0.00808
t=18 | add 0.10899 => Tn=0.99113 error=0.00887 | d_error: -0.00951
t=19 | add 0.10727 => Tn=0.99840 error=0.00160 | d_error: -0.00899
"""

2.4 PID算法总结

for kp_i in np.linspace(0, 1, 10): pid_plot(kp=kp_i, ki=0.2, kd=0.2)

for ki_i in np.linspace(0, 1, 10): pid_plot(kp=0.5, ki=ki_i, kd=0.2)

for kd_i in np.linspace(0, 1, 10): pid_plot(kp=0.5, ki=0.2, kd=kd_i)

pid_plot(kp=0.65, ki=0.05, kd=0.5, print_flag=True)

三、牛顿法调参

损失函数采用：RMSE

from scipy import optimize 
import matplotlib.pyplot as plt
import numpy as np

def pid_plot(args, plot_flag=True, print_flag=False):
    kp, ki, kd = args
    T=1
    Tn=0.2
    error=1-0.2
    extra_drop = 0.1
    sum_error = 0
    d_error = 0
    error_n = 0
    error_b = 0
    Tn_list = []
    for t in range(1, 100):
        error_b = error_n
        error_n = error
        d_error = error_n - error_b if t >= 2 else 0
        sum_error += error
        U = kp * error + ki * sum_error + kd * d_error
        Tn += U - extra_drop
        error = T-Tn
        Tn_list.append(Tn)
        if print_flag:
            print(f't={t} | add {U:.5f} => Tn={Tn:.5f} error={error:.5f} | d_error: {d_error:.5f}')

    if plot_flag:
        plt.plot(Tn_list)
        plt.axhline(1, linestyle='--', color='darkred', alpha=0.8)
        plt.title(f'$K_p$={kp:.3f} $K_i$={ki:.3f} $K_d$={kd:.3f}')
        plt.ylim([0, max(Tn_list) + 0.2])
        plt.show()

    loss = np.sqrt(np.mean(np.square(np.ones_like(Tn_list) - np.array(Tn_list))))
    return loss



boundaries=[(0, 2), (0, 2), (0, 2)]
res = optimize.fmin_l_bfgs_b(pid_plot, np.array([0.1, 0.1, 0.1]), args=(False, False), bounds = boundaries, approx_grad = True)

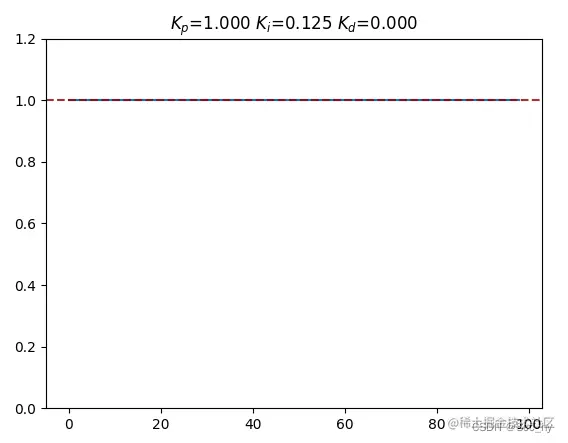
pid_plot(res[0].tolist(), print_flag=True)
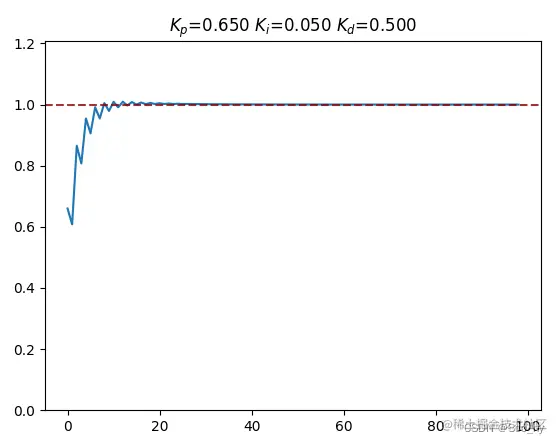
pid_plot([0.65, 0.05, 0.5], print_flag=True)

牛顿法调参结果图示：