Python 官方文档:入门教程 => 点击学习
一、使用sklearn转换器处理 sklearn提供了model_selection模型选择模块、preprocessing数据预处理模块、decompisition特征分
sklearn提供了model_selection模型选择模块、preprocessing数据预处理模块、decompisition特征分解模块,通过这三个模块能够实现数据的预处理和模型构建前的数据标准化、二值化、数据集的分割、交叉验证和PCA降维处理等工作。
sklearn库的datasets模块集成了部分数据分析的经典数据集,可以选用进行数据预处理、建模的操作。
常见的数据集加载函数(器):
数据集加载函数(器) | 数据集任务类型 |
load_digits | 分类 |
load_wine | 分类 |
load_iris | 分类、聚类 |
load_breast_cancer | 分类、聚类 |
load_boston | 回归 |
fetch_california_housing | 回归 |
加载后的数据集可以看成是一个字典,几乎所有的sklearn数据集均可以使用data、target、feature_names、DESCR分别获取数据集的数据、标签、特征名称、描述信息。
以load_breast_cancer为例:
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()##将数据集赋值给iris变量
print('breast_cancer数据集的长度为:',len(cancer))
print('breast_cancer数据集的类型为:',type(cancer))
#breast_cancer数据集的长度为: 6
#breast_cancer数据集的类型为: <class 'sklearn.utils.Bunch'>
cancer_data = cancer['data']
print('breast_cancer数据集的数据为:','\n',cancer_data)
#breast_cancer数据集的数据为:
[[1.799e+01 1.038e+01 1.228e+02 ... 2.654e-01 4.601e-01 1.189e-01]
[2.057e+01 1.777e+01 1.329e+02 ... 1.860e-01 2.750e-01 8.902e-02]
[1.969e+01 2.125e+01 1.300e+02 ... 2.430e-01 3.613e-01 8.758e-02]
...
[1.660e+01 2.808e+01 1.083e+02 ... 1.418e-01 2.218e-01 7.820e-02]
[2.060e+01 2.933e+01 1.401e+02 ... 2.650e-01 4.087e-01 1.240e-01]
[7.760e+00 2.454e+01 4.792e+01 ... 0.000e+00 2.871e-01 7.039e-02]]
cancer_target = cancer['target'] ## 取出数据集的标签
print('breast_cancer数据集的标签为:\n',cancer_target)
#breast_cancer数据集的标签为:
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 0 0 0 0 0 0 0 0 1 0 1 1 1 1 1 0 0 1 0 0 1 1 1 1 0 1 0 0 1 1 1 1 0 1 0 0
1 0 1 0 0 1 1 1 0 0 1 0 0 0 1 1 1 0 1 1 0 0 1 1 1 0 0 1 1 1 1 0 1 1 0 1 1
1 1 1 1 1 1 0 0 0 1 0 0 1 1 1 0 0 1 0 1 0 0 1 0 0 1 1 0 1 1 0 1 1 1 1 0 1
1 1 1 1 1 1 1 1 0 1 1 1 1 0 0 1 0 1 1 0 0 1 1 0 0 1 1 1 1 0 1 1 0 0 0 1 0
1 0 1 1 1 0 1 1 0 0 1 0 0 0 0 1 0 0 0 1 0 1 0 1 1 0 1 0 0 0 0 1 1 0 0 1 1
1 0 1 1 1 1 1 0 0 1 1 0 1 1 0 0 1 0 1 1 1 1 0 1 1 1 1 1 0 1 0 0 0 0 0 0 0
0 0 0 0 0 0 0 1 1 1 1 1 1 0 1 0 1 1 0 1 1 0 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1
1 0 1 1 0 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 0 1 0 1 1 1 1 0 0 0 1 1
1 1 0 1 0 1 0 1 1 1 0 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1 1 1 1 1 1 0 0 1 0 0
0 1 0 0 1 1 1 1 1 0 1 1 1 1 1 0 1 1 1 0 1 1 0 0 1 1 1 1 1 1 0 1 1 1 1 1 1
1 0 1 1 1 1 1 0 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 0 1 0 0 1 0 1 1 1 1 1 0 1 1
0 1 0 1 1 0 1 0 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 0 1
1 1 1 1 1 1 0 1 0 1 1 0 1 1 1 1 1 0 0 1 0 1 0 1 1 1 1 1 0 1 1 0 1 0 1 0 0
1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 0 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 0 0 0 0 0 0 1]
cancer_names = cancer['feature_names'] ## 取出数据集的特征名
print('breast_cancer数据集的特征名为:\n',cancer_names)
#breast_cancer数据集的特征名为:
['mean radius' 'mean texture' 'mean perimeter' 'mean area'
'mean smoothness' 'mean compactness' 'mean concavity'
'mean concave points' 'mean symmetry' 'mean fractal dimension'
'radius error' 'texture error' 'perimeter error' 'area error'
'smoothness error' 'compactness error' 'concavity error'
'concave points error' 'symmetry error' 'fractal dimension error'
'worst radius' 'worst texture' 'worst perimeter' 'worst area'
'worst smoothness' 'worst compactness' 'worst concavity'
'worst concave points' 'worst symmetry' 'worst fractal dimension']
cancer_desc = cancer['DESCR'] ## 取出数据集的描述信息
print('breast_cancer数据集的描述信息为:\n',cancer_desc)
#breast_cancer数据集的描述信息为:
.. _breast_cancer_dataset:
Breast cancer wisconsin (diagnostic) dataset
--------------------------------------------
**Data Set Characteristics:**
:Number of Instances: 569
:Number of Attributes: 30 numeric, predictive attributes and the class
:Attribute InfORMation:
- radius (mean of distances from center to points on the perimeter)
- texture (standard deviation of gray-scale values)
- perimeter
- area
- smoothness (local variation in radius lengths)
- compactness (perimeter^2 / area - 1.0)
- concavity (severity of concave portions of the contour)
- concave points (number of concave portions of the contour)
- symmetry
- fractal dimension ("coastline approximation" - 1)
The mean, standard error, and "worst" or largest (mean of the three
largest values) of these features were computed for each image,
resulting in 30 features. For instance, field 3 is Mean Radius, field
13 is Radius SE, field 23 is Worst Radius.
- class:
- WDBC-Malignant
- WDBC-Benign
:Summary Statistics:
===================================== ====== ======
Min Max
===================================== ====== ======
radius (mean): 6.981 28.11
texture (mean): 9.71 39.28
perimeter (mean): 43.79 188.5
area (mean): 143.5 2501.0
smoothness (mean): 0.053 0.163
compactness (mean): 0.019 0.345
concavity (mean): 0.0 0.427
concave points (mean): 0.0 0.201
symmetry (mean): 0.106 0.304
fractal dimension (mean): 0.05 0.097
radius (standard error): 0.112 2.873
texture (standard error): 0.36 4.885
perimeter (standard error): 0.757 21.98
area (standard error): 6.802 542.2
smoothness (standard error): 0.002 0.031
compactness (standard error): 0.002 0.135
concavity (standard error): 0.0 0.396
concave points (standard error): 0.0 0.053
symmetry (standard error): 0.008 0.079
fractal dimension (standard error): 0.001 0.03
radius (worst): 7.93 36.04
texture (worst): 12.02 49.54
perimeter (worst): 50.41 251.2
area (worst): 185.2 4254.0
smoothness (worst): 0.071 0.223
compactness (worst): 0.027 1.058
concavity (worst): 0.0 1.252
concave points (worst): 0.0 0.291
symmetry (worst): 0.156 0.664
fractal dimension (worst): 0.055 0.208
===================================== ====== ======
:Missing Attribute Values: None
:Class Distribution: 212 - Malignant, 357 - Benign
:Creator: Dr. William H. Wolberg, W. Nick Street, Olvi L. Mangasarian
:Donor: Nick Street
:Date: November, 1995
This is a copy of UCI ML Breast Cancer Wisconsin (Diagnostic) datasets.
https://Goo.gl/U2Uwz2
Features are computed from a digitized image of a fine needle
aspirate (FNA) of a breast mass. They describe
characteristics of the cell nuclei present in the image.
Separating plane described above was obtained using
Multisurface Method-Tree (MSM-T) [K. P. Bennett, "Decision Tree
Construction Via Linear Programming." Proceedings of the 4th
Midwest Artificial Intelligence and Cognitive Science Society,
pp. 97-101, 1992], a classification method which uses linear
programming to construct a decision tree. Relevant features
were selected using an exhaustive search in the space of 1-4
features and 1-3 separating planes.
The actual linear program used to obtain the separating plane
in the 3-dimensional space is that described in:
[K. P. Bennett and O. L. Mangasarian: "Robust Linear
Programming Discrimination of Two Linearly Inseparable Sets",
Optimization Methods and Software 1, 1992, 23-34].
This database is also available through the UW CS ftp server:
ftp ftp.cs.wisc.edu
cd math-prog/cpo-dataset/Machine-learn/WDBC/
.. topic:: References
- W.N. Street, W.H. Wolberg and O.L. Mangasarian. Nuclear feature extraction
for breast tumor diagnosis. IS&T/SPIE 1993 International Symposium on
Electronic Imaging: Science and Technology, volume 1905, pages 861-870,
San Jose, CA, 1993.
- O.L. Mangasarian, W.N. Street and W.H. Wolberg. Breast cancer diagnosis and
prognosis via linear programming. Operations Research, 43(4), pages 570-577,
July-August 1995.
- W.H. Wolberg, W.N. Street, and O.L. Mangasarian. Machine learning techniques
to diagnose breast cancer from fine-needle aspirates. Cancer Letters 77 (1994)
163-171.在数据分析的过程中,为了保证模型在实际系统中能够起到预期的作用,一般需要将样本分成独立的三部分:训练集(train set)、验证集(validation set)、测试集(test set)。
训练集—50%:用于估计模型
验证集—25%:用于确定网络结构或控制模型复杂程度的参数
测试集—25%:用于检验最优模型的性能
当数据总量较少的时候,使用上述方法划分就不合适。常用的方法是留少部分做测试集,然后对其余N个样本采用K折交叉验证法:
将样本打乱,并均匀分成K份,轮流选择其中K-1份做训练,剩余一份做检验,计算预测误差平方和,最后把K次的预测误差平方和的均值作为选择最优模型结构的依据。
sklearn.model_selection.train_test_split(*arrays,**options)参数名称 | 说明 |
*arrays | 接受一个或者多个数据集。代表需要划分的数据集。若为分类、回归,则传入数据、标签;若为聚类,则传入数据 |
test_size | 代表测试集的大小。若传入为float类型数据,需要限定在0-1之间,代表测试集在总数中的占比;若传入的为int型数据,则表示测试集记录的绝对数目。该参数与train_size可以只传入一个。 |
train_size | 与test_size相同 |
random_state | 接受int。代表随机种子编号,相同随机种子编号产生相同的随机结果。 |
shuffle | 接受boolean。代表是否进行有回放抽样,若为True,则stratify参数必须不能为空。 |
stratify | 接受array或None。若不为None,则使用传入的标签进行分层抽样。 |
print('原始数据集数据的形状为:',cancer_data.shape)
print('原始数据集标签的形状为:',cancer_target.shape)
原始数据集数据的形状为: (569, 30)
原始数据集标签的形状为: (569,)
from sklearn.model_selection import train_test_split
cancer_data_train,cancer_data_test,cancer_target_train,cancer_target_test = train_test_split(cancer_data,cancer_target,
test_size=0.2,random_state=42)
print('训练集数据的形状为:',cancer_data_train.shape)
print('训练集数据的标签形状为:',cancer_target_train.shape)
print('测试集数据的形状为:',cancer_data_test.shape)
print('测试集数据的标签形状为:',cancer_target_test.shape)
训练集数据的形状为: (455, 30)
训练集数据的标签形状为: (455,)
测试集数据的形状为: (114, 30)
测试集数据的标签形状为: (114,)该函数分别将传入的数据划分为训练集和测试集。如果传入的是一组数据,那么生成的就是这一组数据随机划分后的训练集和测试集,总共两组;如果传入的是两组数据,那么生成的训练集和测试集分别两组,总共四组。train_test_split方法仅是最常用的数据划分方法,在model_selection模块中还有其他的划分函数,例如PredefinedSplit、ShuffleSplit等。
sklearn将相关的功能封装为转换器,转换器主要包含有3个方法:fit、transform、fit_trainsform:

import numpy as np
from sklearn.preprocessing import MinMaxScaler
# 生成规则
Scaler = MinMaxScaler().fit(cancer_data_train)
# 将规则应用于训练集
cancer_trainScaler = Scaler.transform(cancer_data_train)
# 将规则应用于测试集
cancer_testScaler = Scaler.transform(cancer_data_test)
print('离差标准化前训练集数据的最小值:',cancer_data_train.min())
print('离差标准化后训练集数据的最小值:',np.min(cancer_trainScaler))
print('离差标准化前训练集数据的最大值:',np.max(cancer_data_train))
print('离差标准化后训练集数据的最大值:',np.max(cancer_trainScaler))
print('离差标准化前测试集数据的最小值:',np.min(cancer_data_test))
print('离差标准化后测试集数据的最小值:',np.min(cancer_testScaler))
print('离差标准化前测试集数据的最大值:',np.max(cancer_data_test))
print('离差标准化后测试集数据的最大值:',np.max(cancer_testScaler))
离差标准化前训练集数据的最小值: 0.0
离差标准化后训练集数据的最小值: 0.0
离差标准化前训练集数据的最大值: 4254.0
离差标准化后训练集数据的最大值: 1.0000000000000002
离差标准化前测试集数据的最小值: 0.0
离差标准化后测试集数据的最小值: -0.057127602776294695
离差标准化前测试集数据的最大值: 3432.0
离差标准化后测试集数据的最大值: 1.3264399566986453目前利用sklearn能够实现对传入的numpy数组进行标准化处理、归一化处理、、二值化处理和PCA降维处理。前面基于pandas库介绍的标准化处理在日常数据分析过程中,各类特征处理相关的操作都需要对训练集和测试集分开进行,需要将训练集中的操作规则、权重系数等应用到测试集中,利用pandas会使得过程繁琐,而sklearn转换器可以轻松实现。
除了上面展示的离差标准化函数MinMaxScaler外,还提供了一系列的数据预处理函数:
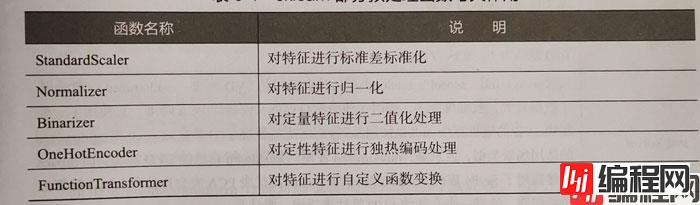
PCA降维处理:
sklearn.decomposition.PCA(n_components=None, *, copy=True, whiten=False, svd_solver='auto', tol=0.0, iterated_power='auto', random_state=None)
from sklearn.decomposition import PCA
# 生成规则
pca_model=PCA(n_components=10).fit(cancer_trainScaler)
# 将规则应用到训练集
cancer_trainPca = pca_model.transform(cancer_trainScaler)
# 将规则应用到测试集
cancer_testPca = pca_model.transform(cancer_testScaler)
print('PCA降维前训练集数据的形状为:',cancer_trainScaler.shape)
print('PCA降维后训练集数据的形状为:',cancer_trainPca.shape)
print('PCA降维前测试集数据的形状为:',cancer_testScaler.shape)
print('PCA降维后测试集数据的形状为:',cancer_testPca.shape)
PCA降维前训练集数据的形状为: (455, 30)
PCA降维后训练集数据的形状为: (455, 10)
PCA降维前测试集数据的形状为: (114, 30)
PCA降维后测试集数据的形状为: (114, 10)聚类分析是在没有给定划分类别的情况下,根据数据相似度进行样本分组的一种方法。
聚类的输入是一组未被标记的样本,聚类根据数据自身的距离或相似度将它们划分为若干组,划分的原则是:组内距离最小化,组间距离最大化。
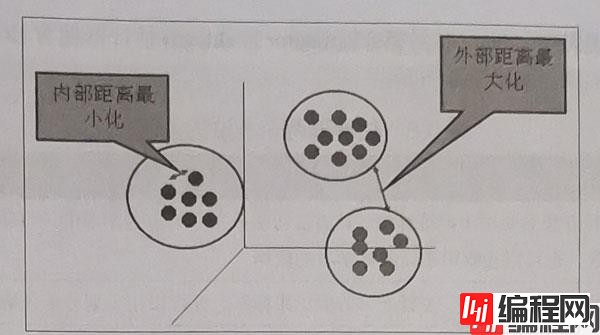

sklearn常用的聚类算法模块cluster提供的聚类算法:
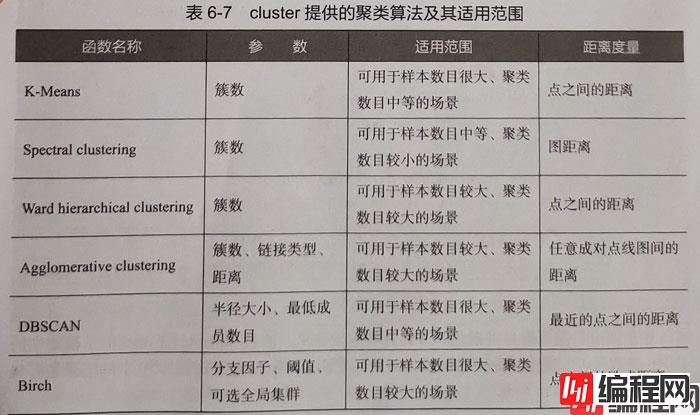
聚类算法的实现需要sklearn估计器(Estimnator),其拥有fit和predict两个方法:
方法名称 | 说明 |
fit | |
predict | 用于预测有监督学习的测试集标签,也可以用于划分传入数据的类别 |
以iris数据为例,使用sklearn估计器构建K-Means聚类模型:
from sklearn.datasets import load_iris
from sklearn.preprocessing import MinMaxScaler
from sklearn.cluster import KMeans
iris = load_iris() # 加载iris数据集
iris_data = iris['data'] # 提取iris数据集中的特征
iris_target = iris['target'] # 提取iris数据集中的标签
iris_feature_names = iris['feature_names'] #提取iris数据集中的特征名称
scale = MinMaxScaler().fit(iris_data) # 对数据集中的特征设定训练规则
iris_dataScale = scale.transform(iris_data) # 应用规则
kmeans = KMeans(n_clusters=3,random_state=123).fit(iris_dataScale) # 构建并训练模型
print('构建的K-Means模型为:\n',kmeans)
#构建的K-Means模型为:
KMeans(algorithm='auto', copy_x=True, init='k-means++', max_iter=300,
n_clusters=3, n_init=10, n_jobs=None, precompute_distances='auto',
random_state=123, tol=0.0001, verbose=0)聚类完成后可以通过sklearn的manifold模块中的TXNE函数实现多维数据的可视化展现。
import pandas as pd
from sklearn.manifold import TSNE
import matplotlib.pyplot as plt
# 使用TSNE进行数据降维,降成2维
tsne = TSNE(n_components=2,init='random',random_state=177).fit(iris_data)
df = pd.DataFrame(tsne.embedding_) # 将原始数据转换为DataFrame
df['labels'] = kmeans.labels_ # 将聚类结果存储进df数据表
# 提取不同标签的数据
df1 = df[df['labels']==0]
df2 = df[df['labels']==1]
df3 = df[df['labels']==2]
# 绘制图形
# 绘制画布大小
fig = plt.figure(figsize=(9,6))
# 用不同颜色表示不同数据
plt.plot(df1[0],df1[1],'bo',df2[0],df2[1],'r*',df3[0],df3[1],'gD')
# 保存图片
plt.savefig('tmp/聚类结果.png')
# 展示
plt.show()聚类评价的标准是组内的对象相互之间是相似的,而不同组间的对象是不同的,即组内相似性越大,组间差别性越大,聚类效果越好。

注意:
1.前四种方法需要真实值的配合才能够评价聚类算法的优劣,更具有说服力,并且在实际操作中,有真实值参考下,聚类方法的评价可以等同于分类算法的评价。
2.除了轮廓系数评价法以外的评价方法,在不考虑业务场景的情况下都是分数越高越好,最高分为1,而轮廓系数评价法需要判断不同类别数目情况下的轮廓系数的走势,寻找最优的聚类数目。
FMI评价法
from sklearn.datasets import load_irisiris = load_iris() # 加载iris数据集iris_data = iris['data'] # 提取数据集特征 iris_target = iris['target'] # 提取数据集标签 from sklearn.metrics import fowlkes_mallows_score from sklearn.cluster import KMeans for i in range(2,7): # 构建并训练模型 kmeans = KMeans(n_clusters=i,random_state=123).fit(iris_data) score = fowlkes_mallows_score(iris_target,kmeans.labels_) print('iris数据聚%d类FMI评价分值为:%f'%(i,score)) iris数据聚2类FMI评价分值为:0.750473 iris数据聚3类FMI评价分值为:0.820808 iris数据聚4类FMI评价分值为:0.756593 iris数据聚5类FMI评价分值为:0.725483 iris数据聚6类FMI评价分值为:0.614345
通过结果可以看出来,当聚类为3时FMI评价分最高,所以当聚类3的时候,K-Means模型最好。
轮廓系数评价法
from sklearn.datasets import load_irisiris = load_iris() # 加载iris数据集iris_data = iris['data'] # 提取数据集特征 iris_target = iris['target'] # 提取数据集标签 from sklearn.metrics import silhouette_score from sklearn.cluster import KMeans import matplotlib.pyplot as plt silhouettteScore = [] for i in range(2,15): ##构建并训练模型 kmeans = KMeans(n_clusters = i,random_state=123).fit(iris_data) score = silhouette_score(iris_data,kmeans.labels_) silhouettteScore.append(score) plt.figure(figsize=(10,6)) plt.plot(range(2,15),silhouettteScore,linewidth=1.5, linestyle="-") plt.show()
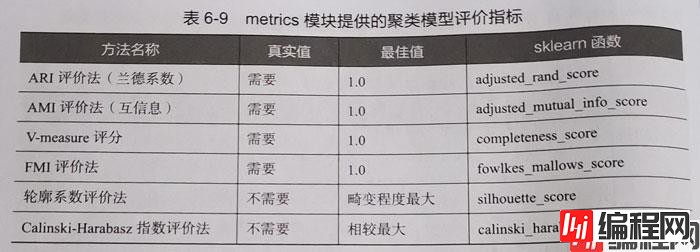
从图形可以看出,聚类数目为2、3和5、6时平均畸变程度最大。由于iris数据本身就是3种鸢尾花的花瓣、花萼长度和宽度的数据,侧面说明了聚类数目为3的时候效果最佳。
Calinski_Harabasz指数评价法
from sklearn.datasets import load_irisiris = load_iris() # 加载iris数据集iris_data = iris['data'] # 提取数据集特征 iris_target = iris['target'] # 提取数据集标签 from sklearn.metrics import silhouette_score from sklearn.cluster import KMeans from sklearn.metrics import calinski_harabasz_score for i in range(2,7): ##构建并训练模型 kmeans = KMeans(n_clusters = i,random_state=123).fit(iris_data) score = calinski_harabasz_score(iris_data,kmeans.labels_) print('iris数据聚%d类calinski_harabaz指数为:%f'%(i,score)) iris数据聚2类calinski_harabaz指数为:513.924546 iris数据聚3类calinski_harabaz指数为:561.627757 iris数据聚4类calinski_harabaz指数为:530.765808 iris数据聚5类calinski_harabaz指数为:495.541488 iris数据聚6类calinski_harabaz指数为:469.836633
同样可以看出在聚类为3时,K-Means模型为最优。综合以上评价方法的使用,在有真实值参考时,几种方法都能有效的展示评估聚合模型;在没有真实值参考时,可以将轮廓系数评价与Calinski_Harabasz指数评价相结合使用。
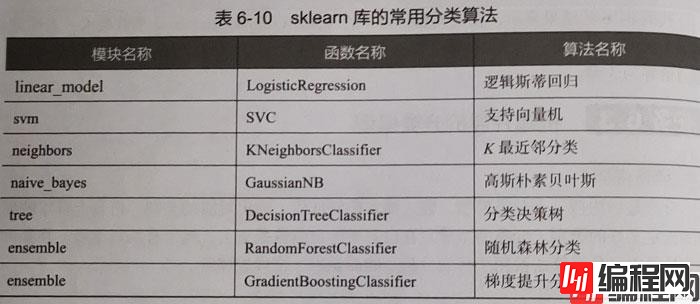
分类是指构造一个分类模型,输入样本的特征值,输出对应类别,将每个样本映射到预先定义好的类别。分类模型是建立在自己已有类标记的数据集上,属于有监督学习。在实际应用场景中,分类算法被应用在行为分析、物品识别、图像检测等。

以breast_cancer数据集为例,使用sklearn估计器构建支持向量机(SVM)模型:
import numpy as np
from sklearn.datasets import load_breast_cancer
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
cancer = load_breast_cancer()
cancer_data = cancer['data']
cancer_target = cancer['target']
cancer_names = cancer['feature_names']
## 将数据划分为训练集测试集
cancer_data_train,cancer_data_test,cancer_target_train,cancer_target_test = \
train_test_split(cancer_data,cancer_target,test_size = 0.2,random_state = 22)
## 数据标准化
stdScaler = StandardScaler().fit(cancer_data_train) # 设定标准化规则
cancer_trainStd = stdScaler.transform(cancer_data_train) # 将标准化规则应用到训练集
cancer_testStd = stdScaler.transform(cancer_data_test) # 将标准化规则应用到测试集
## 建立SVM模型
svm = SVC().fit(cancer_trainStd,cancer_target_train)
print('建立的SVM模型为:\n',svm)
#建立的SVM模型为:
SVC(C=1.0, break_ties=False, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape='ovr', degree=3, gamma='scale', kernel='rbf',
max_iter=-1, probability=False, random_state=None, shrinking=True,
tol=0.001, verbose=False)
## 预测训练集结果
cancer_target_pred = svm.predict(cancer_testStd)
print('预测前20个结果为:\n',cancer_target_pred[:20])
#预测前20个结果为:
[1 0 0 0 1 1 1 1 1 1 1 1 0 1 1 1 0 0 1 1]## 求出预测和真实一样的数目
true = np.sum(cancer_target_pred == cancer_target_test )
print('预测对的结果数目为:', true)
print('预测错的的结果数目为:', cancer_target_test.shape[0]-true)
print('预测结果准确率为:', true/cancer_target_test.shape[0])
预测对的结果数目为: 111
预测错的的结果数目为: 3
预测结果准确率为: 0.9736842105263158分类模型对测试集进行预测而得出的准确率并不能很好地反映模型的性能,为了有效判断一个预测模型的性能表现,需要结合真实值计算出精确率、召回率、F1值、Cohen’s Kappa系数等指标来衡量。
使用单一评价指标(Precision、Recall、F1值、Cohen’s Kappa系数)
from sklearn.metrics import accuracy_score,precision_score,recall_score,f1_score,cohen_kappa_scoreprint('使用SVM预测breast_cancer数据的准确率为:', accuracy_score(cancer_target_test,cancer_target_pred)) print('使用SVM预测breast_cancer数据的精确率为:', precision_score(cancer_target_test,cancer_target_pred)) print('使用SVM预测breast_cancer数据的召回率为:', recall_score(cancer_target_test,cancer_target_pred)) print('使用SVM预测breast_cancer数据的F1值为:', f1_score(cancer_target_test,cancer_target_pred)) print('使用SVM预测breast_cancer数据的Cohen’s Kappa系数为:', cohen_kappa_score(cancer_target_test,cancer_target_pred)) 使用SVM预测breast_cancer数据的准确率为: 0.9736842105263158 使用SVM预测breast_cancer数据的精确率为: 0.9594594594594594 使用SVM预测breast_cancer数据的召回率为: 1.0 使用SVM预测breast_cancer数据的F1值为:0.9793103448275862 使用SVM预测breast_cancer数据的Cohen’s Kappa系数为: 0.9432082364662903
sklearn模块除了提供了Precision等单一评价指标外,还提供了一个能够输出分类模型评价报告的函数classification_report:
python sklearn.metrics.classification_report(y_true, y_pred, *, labels=None, target_names=None, sample_weight=None, digits=2, output_dict=False, zero_division='warn')print('使用SVM预测iris数据的分类报告为:\n', classification_report(cancer_target_test,cancer_target_pred))#使用SVM预测iris数据的分类报告为: precision recall f1-score support 0 1.00 0.93 0.96 43 1 0.96 1.00 0.98 71 accuracy 0.97 114 macro avg 0.98 0.97 0.97 114 weighted avg 0.97 0.97 0.97 114
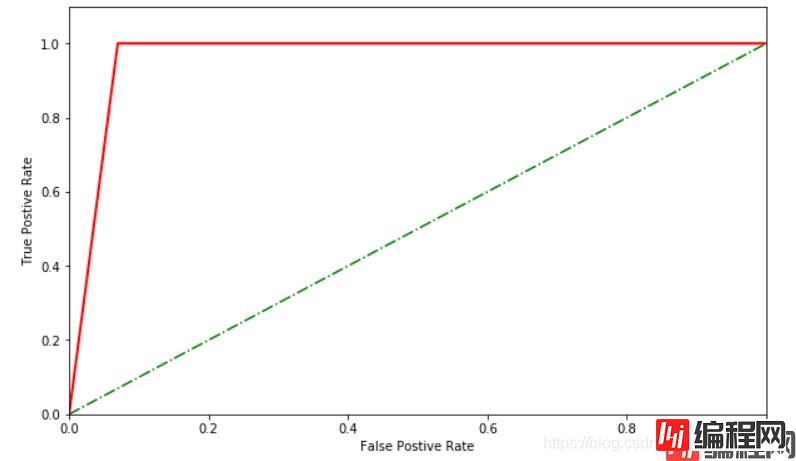
绘制ROC曲线
from sklearn.metrics import roc_curve import matplotlib.pyplot as plt## 求出ROC曲线的x轴和y轴 fpr, tpr, thresholds = roc_curve(cancer_target_test,cancer_target_pred) # 设置画布 plt.figure(figsize=(10,6)) plt.xlim(0,1) ##设定x轴的范围 plt.ylim(0.0,1.1) ## 设定y轴的范围 plt.xlabel('FalsePostive Rate') plt.ylabel('True Postive Rate') x = [0,0.2,0.4,0.6,0.8,1] y = [0,0.2,0.4,0.6,0.8,1] # 绘图 plt.plot(x,y,linestyle='-.',color='green') plt.plot(fpr,tpr,linewidth=2, linestyle="-",color='red') # 展示 plt.show()

ROC曲线横纵坐标范围是[0,1],通常情况下,ROC曲线与x轴形成的面积越大,表示模型性能越好。当ROC曲线如虚线所示时,表明模型的计算结果基本都是随机得来的,此时模型起到的作用几乎为0.
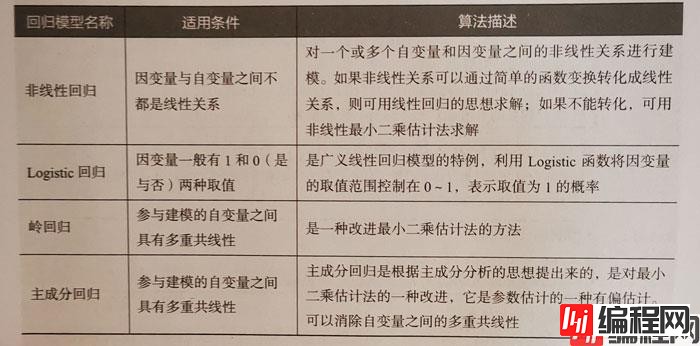
回归算法的实现过程与分类算法相似,原理相差不大。分类和回归的主要区别在于,分类算法的标签是离散的,但是回归算法的标签是连续的。回归算法在交通、物流、社交、网络等领域发挥作用巨大。
在回归模型中,自变量和因变量具有相关关系,自变量的值是已知的,因变量的值是要预测的。回归算法的实现步骤和分类算法基本相同,分为学习和预测两个步骤。
学习:通过训练样本来拟合回归方程
预测:利用学习过程中拟合出的方程,将测试数据放入方程中求出预测值。


from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
# 加载boston数据集
boston = load_boston()
# 提取数据
x = boston['data']
y = boston['target']
names = boston['feature_names']
# 将数据划分为训练集和测试集
x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.2,random_state=125)
# 建立线性回归模型
clf = LinearRegression().fit(x_train,y_train)
print('建立的Linear Regression模型为:\n',clf)
#建立的 Linear Regression模型为:
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False)
# 预测测试集结果
y_pred = clf.predict(x_test)
print('预测前20个结果为:\n',y_pred[:20])
#预测前20个结果为:
[21.16289134 19.67630366 22.02458756 24.61877465 14.44016461 23.32107187
16.64386997 14.97085403 33.58043891 17.49079058 25.50429987 36.60653092
25.95062329 28.49744469 19.35133847 20.17145783 25.97572083 18.26842082
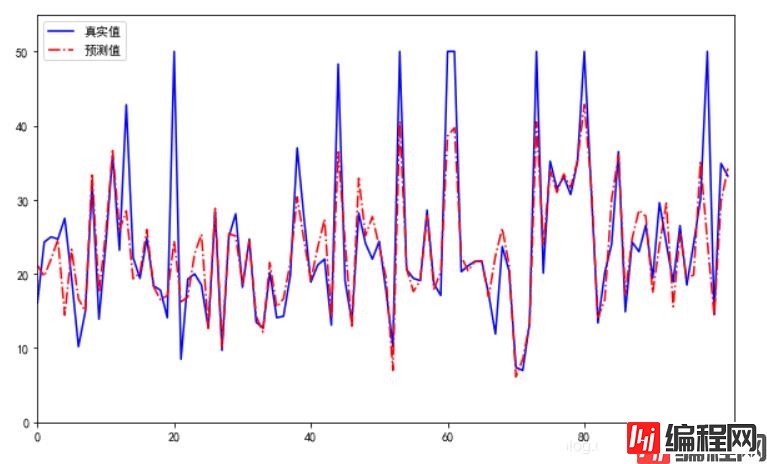
16.52840639 17.08939063]回归结果可视化
# 回归结果可视化
import matplotlib.pyplot as plt
from matplotlib import rcParams
# 设置中文显示
rcParams['font.sans-serif'] = 'SimHei'
# 设置画布
plt.figure(figsize=(10,6))
# 绘图
plt.plot(range(y_test.shape[0]),y_test,color='blue',linewidth=1.5,linestyle='-')
plt.plot(range(y_test.shape[0]),y_pred,color='red',linewidth=1.5,linestyle='-.')
# 设置图像属性
plt.xlim((0,102))
plt.ylim((0,55))
plt.legend(['真实值','预测值'])
# 保存图片
plt.savefig('tmp/聚回归类结果.png')
#展示
plt.show()
回归模型的性能评价不同于分类模型,虽然都是对照真实值进行评价,但是由于回归模型的预测结果和真实值都是连续地,所以不能够用之前的精确率、召回率、F1值进行评价。
使用explained_variance_score, mean_absolute_error, mean_squared_error, r2_score, median_absolute_error进行回归评价
from sklearn.metrics import explained_variance_score,mean_absolute_error,mean_squared_error,\median_absolute_error,r2_score print('Boston数据线性回归模型的平均绝对误差为:', mean_absolute_error(y_test,y_pred)) print('Boston数据线性回归模型的均方误差为:', mean_squared_error(y_test,y_pred)) print('Boston数据线性回归模型的中值绝对误差为:', median_absolute_error(y_test,y_pred)) print('Boston数据线性回归模型的可解释方差值为:', explained_variance_score(y_test,y_pred)) print('Boston数据线性回归模型的R方值为:', r2_score(y_test,y_pred)) #Boston数据线性回归模型的平均绝对误差为: 3.3775517360082032 #Boston数据线性回归模型的均方误差为: 31.15051739031563 #Boston数据线性回归模型的中值绝对误差为: 1.7788996425420773 #Boston数据线性回归模型的可解释方差值为: 0.710547565009666 #Boston数据线性回归模型的R方值为: 0.7068961686076838
到此这篇关于Python数据分析之使用scikit-learn构建模型的文章就介绍到这了,更多相关Python scikit-learn构建模型内容请搜索编程网以前的文章或继续浏览下面的相关文章希望大家以后多多支持编程网!
--结束END--
本文标题: Python数据分析之使用scikit-learn构建模型
本文链接: https://lsjlt.com/news/120052.html(转载时请注明来源链接)
有问题或投稿请发送至: 邮箱/279061341@qq.com QQ/279061341
2024-03-01
2024-03-01
2024-03-01
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
2024-02-29
回答
回答
回答
回答
回答
回答
回答
回答
回答
回答
0